By making use of the MHD self-induction equation in general relativity (GR), recently derived by Clarkson and Marklund (2005), it is shown that when Friedmann universe possesses a spatial section whose Riemannian curvature is negative, the magnetic energy bounds computed by Nuñez (2002) also bounds the growth rate of the magnetic field given by the strain matrix of dynamo flow. Since in GR-MHD dynamo equation, the Ricci tensor couples with the universe magnetic field, only through diffusion, and most ages are highly conductive the interest is more theoretical here, and only very specific plasma astrophysical problems can be address such as in laboratory plasmas. Magnetic fields and the negative curvature of some isotropic cosmologies, contribute to enhence the amplification of the magnetic field. Ricci curvature energy is shown to add to strain matrix of the flow, to enhance dynamo action in the universe. Magnetic fluctuations of the Clarkson-Marklund equations for a constant magnetic field seed in highly conductive flat universes, leads to a magnetic contrast of 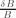≈ 2, which is well within observational limits from extragalactic radiosources of 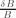≈ 1.7. In the magnetic helicity fluctuations the magnetic contrast shows that the dynamo effects can be driven by these fluctuations.