Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-19T13:38:06.606Z Has data issue: false hasContentIssue false
  • English
  • Français

A Fast Explicit Scheme for Solving MHD Equations with Ambipolar Diffusion

Published online by Cambridge University Press:  27 April 2011

Jongsoo Kim
Jongsoo Kim*
Affiliation:
Korea Astronomy and Space Science Institute, Daejeon 305-348, Republic of Korea email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We developed a fast numerical scheme for solving ambipolar diffusion MHD equations with the strong coupling approximation, which can be written as the ideal MHD equations with an additional ambipolar diffusion term in the induction equation. The mass, momentum, magnetic fluxes due to the ideal MHD equations can be easily calculated by any Godunov-type schemes. Additional magnetic fluxes due to the ambipolar diffusion term are added in the magnetic fluxes, because of two same spatial gradients operated on the advection fluxes and the ambipolar diffusion term. In this way, we easily kept divergence-free magnetic fields using the constraint transport scheme. In order to overcome a small time step imposed by ambipolar diffusion, we used the super time stepping method. The resultant scheme is fast and robust enough to do the long term evolution of star formation simulations. We also proposed that the decay of alf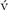en by ambipolar diffusion be a good test problem for our codes.

Keywords

methods:numericalMHDstars: formation
Type
Contributed Papers
Information
Proceedings of the International Astronomical Union , Volume 6 , Symposium S270: Computational Star Formation , May 2010 , pp. 415 - 419
Copyright
Copyright © International Astronomical Union 2011

References

Alexiades, V., Amiez, G., & Gremaud, P.-A. 1996, Comm. Num. Meth. Eng., 12, 313.0.CO;2-5>CrossRefGoogle Scholar
Balsara, D. S. & Spicer, D. S. 1999, J. Comput. Phys., 149, 270CrossRefGoogle Scholar
Choi, E., Kim, J., & Wiita, P. J. 2009, ApJS, 181, 413CrossRefGoogle Scholar
Falle, S. A. E. G. 2003, MNRAS, 344, 1210CrossRefGoogle Scholar
Kim, J., Ryu, D., Jones, T. W., & Hong, S. S. 1999, ApJ, 514, 506CrossRefGoogle Scholar
Li, P. S., McKee, C. F., & Klein, R. I. 2006, ApJ, 653, 1280CrossRefGoogle Scholar
Mac Low, M.-M., Norman, M. L., Königl, A., & Wardle, M. 1995, ApJ, 442, 726CrossRefGoogle Scholar
Mac Low, M.-M. & Smith, M. D. 1997, ApJ, 491, 596CrossRefGoogle Scholar
Mestel, L. & Spitzer, L. Jr. 1956, MNRAS, 116, 503CrossRefGoogle Scholar
Mouschovias, T. Ch. 1987, in: Morfill, G. E. & Scholer, M. (eds.), The Origin of Stars and Planetary Systems, (Dordrecht: Reidel), p. 453Google Scholar
O'Sullivan, S. & Downes, T. P. 2006, MNRAS, 366, 1329CrossRefGoogle Scholar
O'Sullivan, S. & Downes, T. P. 2007, MNRAS, 376, 1648CrossRefGoogle Scholar
Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARAA, 25, 23CrossRefGoogle Scholar
Smith, M. D. & Mac Low, M.-M. 1997, A&A, 326, 801Google Scholar
Stone, J. M. 1997, ApJ, 487, 271CrossRefGoogle Scholar
Tilley, D. A. & Balsara, D. S. 2008, MNRAS, 389, 1058CrossRefGoogle Scholar
Tóth, G. 2000, J. Comput. Phys., 161, 605CrossRefGoogle Scholar