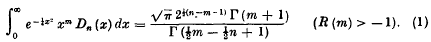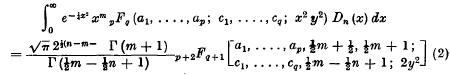Research Article
On certain infinite integrals involving Struve functions and parabolic cylinder functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 171-173
-
- Article
-
- You have access
- Export citation
The place of Dirac's Equation in Five-Dimensional Riemannian Geometry
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 174-182
-
- Article
-
- You have access
- Export citation
The configuration determined by five generators of a quadric threefold
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 183-195
-
- Article
-
- You have access
- Export citation
On compound permutation matrices
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 196-203
-
- Article
-
- You have access
- Export citation
Errata
Errata
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 204
-
- Article
-
- You have access
- Export citation
Index to Papers
Index of Papers Published in this Volume Arranged According to Names of Authors
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 205
-
- Article
-
- You have access
- Export citation
Index According to Subjects
Index According to Subjects
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 206
-
- Article
-
- You have access
- Export citation
Other
Edinburgh Mathematical Society
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 207-214
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 7 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PEM volume 7 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. b1-b5
-
- Article
-
- You have access
- Export citation