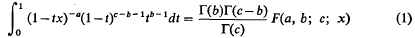Research Article
Group algebras of some generalised soluble groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-5
-
- Article
-
- You have access
- Export citation
The weak-star closure of the unit ball in a hyperplane
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 7-11
-
- Article
-
- You have access
- Export citation
On (J, pn)-summability of Fourier series
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 13-17
-
- Article
-
- You have access
- Export citation
Sequences in genetic algebras for overlapping generations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 19-29
-
- Article
-
- You have access
- Export citation
Some inequalities for a hypergeometric integral
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 31-34
-
- Article
-
- You have access
- Export citation
On well-bounded operators of type (B)
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 35-48
-
- Article
-
- You have access
- Export citation
Varieties of topological groups generated by Lie groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 49-53
-
- Article
-
- You have access
- Export citation
Some axially symmetric potential problems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 55-76
-
- Article
-
- You have access
- Export citation
Self-adjoint square roots of positive self-adjoint bounded linear operators
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 77-79
-
- Article
-
- You have access
- Export citation
Divisibility of ordered groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 81-83
-
- Article
-
- You have access
- Export citation
Book Reviews
J. Duncan, The Elements of Complex Analysis (Wiley, 1968), 313 pp., £4·25; paper, £2·25.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 85
-
- Article
-
- You have access
- Export citation
G. H. Fullerton, Mathematical Analysis (Oliver and Boyd, 1972), 152 pp., £1·75.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 85-86
-
- Article
-
- You have access
- Export citation
R. G. Meadows and R. Delbourgo, Advanced Pure Mathematics (Penguin, 1971), 128 pp., £2
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 86
-
- Article
-
- You have access
- Export citation
M. L. Puri (Editor), Non-Parametric Techniques in Statistical Inference (Cambridge University Press, 1970, xiv + 623 pp., £10·20.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 86-87
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 18 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation