Research Article
A Derivation of Certain Variational Principles for Mixed Boundary Value Problems in Potential Theory
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 113-117
-
- Article
-
- You have access
- Export citation
A Multiplying Factor Method for the Solution of Wiener-Hopf Equations†
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 119-122
-
- Article
-
- You have access
- Export citation
Decomposition of the n-Dimensional Lattice-Graph into Hamiltonian Lines
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 123-131
-
- Article
-
- You have access
- Export citation
Some Finite Analogues of the Poisson Summation Formula†
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 133-138
-
- Article
-
- You have access
- Export citation
A Cyclic Inequality
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 139-147
-
- Article
-
- You have access
- Export citation
The Spectral Sequence of a Covering
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 149-158
-
- Article
-
- You have access
- Export citation
Book Reviews
Paul R. Halmos, Naive Set Theory (Van Nostrand, Princeton, 1960), 26s. 6d.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 159
-
- Article
-
- You have access
- Export citation
E. J. Mcshane, and T. Botts, Real Analysis (van Nostrand, 1959), 272 pp., 49s. 6d.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 159-160
-
- Article
-
- You have access
- Export citation
J. M. Hyslop, Real Variable (University Mathematical Texts Series, Oliver and Boyd, 1960), viii + 136 pp., 8s. 6d.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 160
-
- Article
-
- You have access
- Export citation
G. H. Hardy, and E. M. Wright, An Introduction to the Theory of Numbers (Fourth Edition) (Clarendon Press: Oxford University Press, 1960), 421 pp., 42s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 161
-
- Article
-
- You have access
- Export citation
Th. Schneider, Introduction aux Nombres Transcendants, translated by P. Eymard (Gauthier-Villars, Paris, 1959), 151 pp., 3500 F.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 161
-
- Article
-
- You have access
- Export citation
G. L. Watson, Integral Quadratic Forms (Cambridge, 1960), pp. viii + 143, 30s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 162
-
- Article
-
- You have access
- Export citation
N. Bourbaki, Eléments de Mathématique I. Les structures fondamentales de l'analyse, Livre II Algèbre, Chapitre 9. Formes sesquilinéaires et formes quadratiques (Actualités Scientifiques et industrielles 1272, Hermann, Paris, 1959), 218 pp., 38s.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 162-163
-
- Article
-
- You have access
- Export citation
H. E. Salzer, C. H. Richards and I. Arsham, Table for the solution of Cubic Equations (McGraw-Hill Book Company, New York, 1958), 161 pp., 50s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 163
-
- Article
-
- You have access
- Export citation
P. J. Hilton and S. Wylie, Homology Theory, an introduction to Algebraic Topology (Cambridge University Press, 1960), 484 pp., 75s.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 163-164
-
- Article
-
- You have access
- Export citation
E. Kreyszig, Differential Geometry (Mathematical Expositions No. 11, Toronto, and Oxford University Press, 1959), pp. xiv + 352, 48s.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 164-165
-
- Article
-
- You have access
- Export citation
J. G. Semple, and G. T. Kneebone, Algebraic Curves (Clarendon Press: Oxford University Press, 1959), 361 pp., 45s.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 165-166
-
- Article
-
- You have access
- Export citation
Margaret M. Gow, A Course in Pure Mathematics (English Universities Press, 1960), 619 pp., 40s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 166
-
- Article
-
- You have access
- Export citation
J. G. Defares, and I. N. Sneddon, An Introduction to the Mathematics of Medicine and Biology (North Holland Publishing Co., Amsterdam, 1960), 663 pp., 94s.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 166-167
-
- Article
-
- You have access
- Export citation
W. J. Cunningham, Introduction to Nonlinear Analysis (McGraw-Hill, New York, 1959), 348 pp., 70s.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 167
-
- Article
-
- You have access
- Export citation

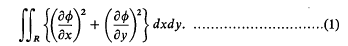




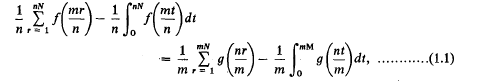
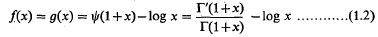
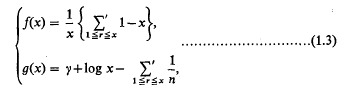
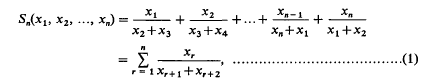
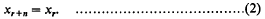
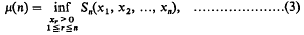
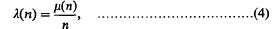
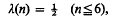
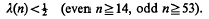
 be a covering of a topological space
be a covering of a topological space  and
and  for some filtration of the graded group
for some filtration of the graded group