Published online by Cambridge University Press: 22 December 2015
Abstract Let G be a linear algebraic group over an algebraically closed field 𝕜 acting rationally on a G-module V with 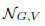 its null-cone. Let δ(G, V) and σ(G, V) denote the minimal number d such that for every
its null-cone. Let δ(G, V) and σ(G, V) denote the minimal number d such that for every 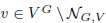 and
and 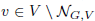 , respectively, there exists a homogeneous invariant f of positive degree at most d such that f(v) ≠ 0. Then δ(G) and σ(G) denote the supremum of these numbers taken over all G-modules V. For positive characteristics, we show that δ(G) = ∞ for any subgroup G of GL2(𝕜) that contains an infinite unipotent group, and σ(G) is finite if and only if G is finite. In characteristic zero, δ(G) = 1 for any group G, and we show that if σ(G) is finite, then G0 is unipotent. Our results also lead to a more elementary proof that βsep(G) is finite if and only if G is finite.
, respectively, there exists a homogeneous invariant f of positive degree at most d such that f(v) ≠ 0. Then δ(G) and σ(G) denote the supremum of these numbers taken over all G-modules V. For positive characteristics, we show that δ(G) = ∞ for any subgroup G of GL2(𝕜) that contains an infinite unipotent group, and σ(G) is finite if and only if G is finite. In characteristic zero, δ(G) = 1 for any group G, and we show that if σ(G) is finite, then G0 is unipotent. Our results also lead to a more elementary proof that βsep(G) is finite if and only if G is finite.