Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T01:02:58.774Z Has data issue: false hasContentIssue false
  • English
  • Français

Young tableaux and longest monotone subsequences: An inequality and a conjecture

Published online by Cambridge University Press:  20 January 2009

A. D. Gordon
A. D. Gordon
Affiliation:
Department of StatisticsUniversity of St. Andrews
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Much work has been done on the following problem, which is sometimes referred to as Ulam's problem: what is the distribution of 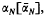, the length (i.e. number of terms) of a longest monotone increasing [decreasing] subsequence of (not necessarily consecutive) terms in a random permutation of the first N integers? For example, it has been shown that 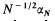converges almost surely to 2 [6,7,9]. In some cases, it is important to know the value of βN(j), the number of permutations for which αN=j

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 27 , Issue 3 , October 1984 , pp. 341 - 344
Copyright
Copyright © Edinburgh Mathematical Society 1984

References

REFERENCES

1.Baer, R. M. and Brock, P., Natural sorting over permutation spaces, Math. Comp. 22 (1968), 385–410.CrossRefGoogle Scholar
2.Berge, C., Principles of Combinatorics (Academic Press, New York and London, 1971).Google Scholar
3.Frame, J. S., DE, G.Robinson, B. and Thrall, R. M., The hook graphs of the symmetric group, Can. J. Math. 6 (1954), 316–324.Google Scholar
4.Gordon, A. D., A measure of the agreement between rankings, Biometrika 66 (1979), 7–15.CrossRefGoogle Scholar
5.Greene, C., Nuenhuis, A. and Wilf, H. S., A probabilistic proof of a formula for the number of Young tableaux of a given shape, Adv. in Math. 31 (1979), 104–109.Google Scholar
6.Hammersley, J. M., A few seedlings of research, Proc. 6th Berkeley Symp. 1 (1972), 345–394.Google Scholar
7.Kesten, H., Contribution to discussion of a paper by J. F. C. Kingman, Ann. Prob. 1 (1973), 903.Google Scholar
8.Schensted, C., Longest increasing and decreasing subsequences, Can. J. Math. 13 (1961), 179–191.CrossRefGoogle Scholar
9.Vershik, A. M. and Kerov, S. V., Asymptotics of the Plancherel measure of the symmetric group and the limiting form of Young tables, Sov. Math. Dokl. 18 (1977), 527–531 (Dokl. Akad. Nauk SSSR 233 (1977), 1024-1027).Google Scholar