Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T02:37:47.855Z Has data issue: false hasContentIssue false
  • English
  • Français

A weight-homogenous condition to the real Jacobian conjecture in $ {\mathbb {R}}^{2}$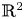

Part of: Partial differential equations Affine geometry General first-order equations and systems

Published online by Cambridge University Press:  19 November 2021

Francisco Braun Open the ORCID record for Francisco Braun [Opens in a new window]  and
Claudia Valls
Francisco Braun
Affiliation:
Departamento de Matemática, Universidade Federal de São Carlos, 13565–905 São Carlos, São Paulo, Brazil ([email protected])
Claudia Valls
Affiliation:
Departamento de Matemática, Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais, 1049–001Lisboa, Portugal ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

It is known that a polynomial local diffeomorphism $(f,\, g): {\mathbb {R}}^{2} \to {\mathbb {R}}^{2}$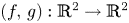 is a global diffeomorphism provided the higher homogeneous terms of $f f_x+g g_x$ 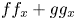and $f f_y+g g_y$ 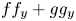do not have real linear factors in common. Here, we give a weight-homogeneous framework of this result. Our approach uses qualitative theory of differential equations. In our reasoning, we obtain a result on polynomial Hamiltonian vector fields in the plane, generalization of a known fact.

Keywords

Real Jacobian conjectureglobal injectivityweight-homogeneous polynomials

MSC classification

Primary: 14R15: Jacobian problem
Secondary: 35F05: Linear first-order equations 35A30: Geometric theory, characteristics, transformations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 4 , November 2021 , pp. 1028 - 1036
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Braun, F. and dos Santos Filho, J. R., The real Jacobian conjecture on $ {\mathbb {R}}^{2}$ is true when one of the components has degree $3$, Discrete Contin. Dyn. Syst. 26 (2010), 75–87.CrossRefGoogle Scholar
Braun, F. and Llibre, J., On the connection between global centers and global injectivity in the plane, arXiv:1706.02643 [math.DS]Google Scholar
Braun, F. and Oréfice-Okamoto, B., On polynomial submersions of degree $4$ and the real Jacobian conjecture in $ {\mathbb {R}}^{2}$, J. Math. Anal. Appl. 443 (2016), 688–706.10.1016/j.jmaa.2016.05.048CrossRefGoogle Scholar
Braun, F., Giné, J. and Llibre, J., A sufficient condition in order that the real Jacobian conjecture in $ {\mathbb {R}}^{2}$ holds, J. Differ. Equ. 260 (2016), 5250–5258.CrossRefGoogle Scholar
Cima, A., Gasull, A. and Mañosas, F., On polynomial Hamiltonian planar vector fields, J. Differ. Equ. 106 (1993), 367–383.CrossRefGoogle Scholar
Cima, A., Gasull, A. and Mañosas, F., Injectivity of polynomial local homeomorphisms of $ {\mathbb {R}}^{n}$, Nonlinear Anal. 26 (1996), 877–885.10.1016/0362-546X(94)00328-FCrossRefGoogle Scholar
Cobo, M., Gutierrez, C. and Llibre, J., On the injectivity of $C^{1}$–maps of the real plane, Canad. J. Math. 54 (2002), 1187–1201.10.4153/CJM-2002-045-0CrossRefGoogle Scholar
Dumortier, F., Llibre, J. and Artés, J. C., Qualitative theory of planar differential systems, Universitext (Springer-Verlag, Berlin, 2006).Google Scholar
van den Essen, A., Polynomial automorphisms and the Jacobian conjecture, Progress in Mathematics, Volume 190 (Birkhäuser Verlag, Basel, 2000).10.1007/978-3-0348-8440-2CrossRefGoogle Scholar
Fernandes, A., Gutierrez, C. and Rabanal, R., Global asymptotic stability for differentiable vector fields of $ {\mathbb {R}}^{2}$, J. Differ. Equ. 206 (2004), 470–482.CrossRefGoogle Scholar
Gavrilov, L., Isochronicity of plane polynomial Hamiltonian systems, Nonlinearity 10 (1997), 433–448.10.1088/0951-7715/10/2/008CrossRefGoogle Scholar
González-Velasco, E. A., Generic properties of polynomial vector fields at infinity, Trans. Amer. Math. Soc. 143 (1969), 201–222.CrossRefGoogle Scholar
Gwoździewicz, J., The real Jacobian conjecture for polynomials of degree 3, Ann. Polon. Math. 76 (2001), 121–125.10.4064/ap76-1-12CrossRefGoogle Scholar
Mello, L. F. and Xavier, F., Dynamics, points and places at infinity, and the inversion of polynomial self-maps of $ {\mathbb {R}}^{2}$, Expo. Math 38 (2020), 365–376.10.1016/j.exmath.2019.03.001CrossRefGoogle Scholar
Pinchuk, S., A counterexample to the strong real Jacobian conjecture, Math. Z. 217 (1994), 1–4.10.1007/BF02571929CrossRefGoogle Scholar
Randall, J. D., The real Jacobian problem, Singularities, Part 2 (Arcata, Calif., 1981), pp. 411–414, Proc. Sympos. Pure Math., Volume 40 (Amer. Math. Soc., Providence, RI, 1983).CrossRefGoogle Scholar
Sabatini, M., A connection between isochronous Hamiltonian centres and the Jacobian conjecture, Nonlinear Anal. 34 (1998), 829–838.10.1016/S0362-546X(97)00604-4CrossRefGoogle Scholar