Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T06:53:45.769Z Has data issue: false hasContentIssue false
  • English
  • Français

The Vibrations of a Particle about a Position of Equilibrium

Published online by Cambridge University Press:  20 January 2009

Bevan B. Baker  and
E. B. Ross
Bevan B. Baker
Affiliation:
Lecturer in Mathematics in the University of Edinburgh
E. B. Ross
Affiliation:
Professor of Mathematics in the Madras Christian College.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. In obtaining a solution of the differential equations corresponding to the motion of a particle about a position of equilibrium, it is usual to express the displacements in terms of a series of periodic terms, each sine or cosine having for its coefficient a series of powers of small quantities. Korteweg has discussed the general form of such solutions, and, from the developments in series which he has obtained, has deduced certain features of interest. In particular, he has shown that, under certain circumstances, it is possible that certain vibrations of higher order, which are normally of small intensity compared with the principal vibrations, may acquire an abnormally large intensity. Considering the oscillations of a dynamical system having a number of degrees of freedom, and supposing 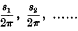to be the frequencies corresponding to infinitesimal oscillations in the different normal coordinates, Korteweg has shown that these cases of interest arise only when

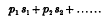
is zero or very small, where p1, p2,… are small integers, positive or negative; the most important cases occur when

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 39 , February 1920 , pp. 34 - 57
Copyright
Copyright © Edinburgh Mathematical Society 1920

References

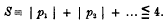
* Korteweg: Archives Néerlandaises des Sciences exactes et naturelles (2), 1, pp. 229–260, 1897.Google Scholar

† H. Beth: Archives Néerlandaises des Sciences exactes et naturelles (2), 15, pp. 246–283, 1910.Google Scholar

* As these values are required with greater accuracy further terms were obtained in the expressions for β1, and β2.