No CrossRef data available.
Article contents
A Version of Hagen's Proof of the “Law of Error.”
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Hagen's proof (1837), as described in the 8th edition of Mansfield Merriman's “Method of Least Squares,” is based on the assumption that the error may be supposed to consist of the algebraic sum of an infinite number of infinitesimal errors of equal amount ε, each one of which is equally likely to be positive or negative. Thus if 2m is the number of the infinitesimal errors, the probability of the error x ≡ 2p ε occurring is
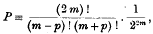
and the maximum value of P occurs when p = 0, and is
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1919
References
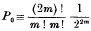* This is equivalent to the assumption that the probability that the error lies between two finite values differing by a finite amount, is finite.
You have
Access