Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Walker, Peter
1997.
Separation of Zeros of Translates of Polynomials and Entire Functions.
Journal of Mathematical Analysis and Applications,
Vol. 206,
Issue. 1,
p.
270.


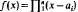 be a polynomial with distinct real zeros whose separation is defined by δ(
be a polynomial with distinct real zeros whose separation is defined by δ(