Hostname: page-component-6dbcb7884d-4kfsg Total loading time: 0 Render date: 2025-02-14T08:44:38.198Z Has data issue: false hasContentIssue false
  • English
  • Français

Upper and lower limit oscillation conditions for first-order difference equations

Part of: Difference equations Difference and functional equations

Published online by Cambridge University Press:  07 July 2022

Özkan Öcalan Open the ORCID record for Özkan Öcalan [Opens in a new window]
Özkan Öcalan*
Affiliation:
Department of Mathematics, Faculty of Science, Akdeniz University, Antalya 07058, Turkey ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, we consider the first-order difference equation with general argument

\[ \varDelta x(n)+p(n)x\left( \tau (n)\right) =0,\quad n\geq 0, \]
where $(p(n))$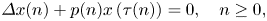 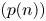is a sequence of non-negative real numbers, $(\tau (n))$ 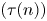is a sequence of integers such that $\tau (n)< n$ 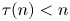for$\ n\in \mathbf {N},\,$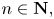and$\ \lim _{n\rightarrow \infty }\tau (n)=\infty.$ 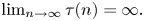Under the assumption that the deviating argument is not necessarily monotone, we obtain some new oscillation conditions and improve the all known results for the above equation in the literature, involving only upper and only lower limit conditions. Two examples illustrating the results are also given.

Keywords

delay difference equationgeneral argumentoscillation

MSC classification

Primary: 39A10: Difference equations, additive 39A21: Oscillation theory
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 3 , August 2022 , pp. 618 - 631
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Braverman, E. and Karpuz, B., On oscillation of differential and difference equations with non-monotone delays, Appl. Math. Comput. 218 (2011), 3880–3887.Google Scholar
Chatzarakis, G. E., Koplatadze, R. and Stavroulakis, I. P., Optimal oscillation criteria for first order difference equations with delay argument, Pacific J. Math. 235 (2008), 15–33.CrossRefGoogle Scholar
Chatzarakis, G. E., Koplatadze, R. and Stavroulakis, I. P., Oscillation criteria of first order linear difference equations with delay argument, Nonlinear Anal. 68 (2008), 994–1005.CrossRefGoogle Scholar
Chatzarakis, G. E., Philos, Ch. G. and Stavroulakis, I. P., On the oscillation of the solutions to linear difference equations with variable delay, Electron. J. Differ. Equ. 50 (2008), 1–5.Google Scholar
Chatzarakis, G. E., Philos, Ch. G. and Stavroulakis, I. P., An oscillation criterion for linear difference equations with general delay argument, Portugal. Math. (N.S.) 66 (4) (2009), 513–533.CrossRefGoogle Scholar
Chen, M. P. and Yu, J. S., Oscillations of delay difference equations with variable coefficients, in Proceedings of the First International Conference on Difference Equations, pp. 105–114 (Gordon and Breach, London, 1994).Google Scholar
Erbe, L. H. and Zhang, B. G., Oscillation of discrete analogues of delay equations, Differ. Int. Equ. 2 (1989), 300–309.Google Scholar
Erbe, L. H., Kong, Q. and Zhang, B. G., Oscillation theory for functional differential equations, (Marcel Dekker, New York, 1995).Google Scholar
Györi, I. and Ladas, G., Linearized oscillations for equations with piecewise constant arguments, Differ. Int. Equ. 2 (1989), 123–131.Google Scholar
Györi, I. and Ladas, G., Oscillation Theory of Delay Differential Equations with Applications (Oxford, Clarendon Press, 1991).Google Scholar
Ladas, G., Explicit conditions for the oscillation of difference equations, J. Math. Anal. Appl 153 (1990), 276–287.CrossRefGoogle Scholar
Ladas, G., Philos, Ch. G. and Sficas, Y. G., Sharp conditions for the oscillation of delay difference equations, J. Appl. Math. Simul. 2 (1989), 101–111.CrossRefGoogle Scholar
Ladde, G. S., Lakshmikantham, V. and Zhang, B. G., Oscillation theory of differential equations with deviating arguments (New York, Marcel Dekker, 1987).Google Scholar
Philos, Ch. G., On oscillations of some difference equations, Funkcial. Ekvac. 34 (1991), 157–172.Google Scholar
Öcalan, Ö., An improved oscillation criterion for first order difference equations, Bull. Math. Soc. Sci. Math. Roumanie (N.S.) 59 (107) (2016), 65–73.Google Scholar
Öcalan, Ö., Oscillation of first-order dynamic equations with nonmonotone delay, Math. Methods Appl. Sci. 43 (2020), 3954–3964.Google Scholar
Yan, W., Meng, Q. and Yan, J., Oscillation criteria for difference equation of variable delays, Dyn. Contin. Discrete Impuls. Syst. Ser. A Math. Anal. 13A (2006), 641–647. Part 2, suppl.Google Scholar
Zhang, B. G. and Tian, C. J., Nonexistence and existence of positive solutions for difference equations with unbounded delay, Comput. Math. Appl. 36 (1998), 1–8.CrossRefGoogle Scholar
Zhang, B. G. and Tian, C. J., Oscillation criteria for difference equations with unbounded delay, Comput. Math. Appl. 35 (4) (1998), 19–26.CrossRefGoogle Scholar