Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hanke, Bernhard
2005.
Geometric versus homotopy theoretic equivariant bordism.
Mathematische Annalen,
Vol. 332,
Issue. 3,
p.
677.
Sinha, Dev
2005.
Bordism of semi-free S1-actions.
Mathematische Zeitschrift,
Vol. 249,
Issue. 2,
p.
439.
Hanke, Bernhard
2008.
Positive scalar curvature with symmetry.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2008,
Issue. 614,
Buchstaber, V.
Panov, T.
and
Ray, N.
2010.
Toric Genera.
International Mathematics Research Notices,
Li, Ping
2011.
The rigidity of Dolbeault-type operators and symplectic circle actions.
Proceedings of the American Mathematical Society,
Vol. 140,
Issue. 6,
p.
1987.
Wiemeler, Michael
2020.
S1-Equivariant bordism, invariant metrics of positive scalar curvature, and rigidity of elliptic genera.
Journal of Topology and Analysis,
Vol. 12,
Issue. 04,
p.
1103.
Jang, Donghoon
2023.
Almost Complex Torus Manifolds—Graphs and Hirzebruch Genera.
International Mathematics Research Notices,
Vol. 2023,
Issue. 17,
p.
14594.
Jang, Donghoon
2024.
Almost complex torus manifolds - a problem of Petrie type.
Proceedings of the American Mathematical Society,
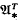 , the bordism module of unitary T-manifolds, where T denotes the circle group S1. We give both an algebraic and a geometric description. The algebraic result is
, the bordism module of unitary T-manifolds, where T denotes the circle group S1. We give both an algebraic and a geometric description. The algebraic result is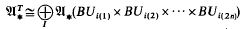
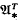 .
.