Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-14T22:28:56.202Z Has data issue: false hasContentIssue false
  • English
  • Français

Two Multiplier Theorems for H1(U2)

Published online by Cambridge University Press:  20 January 2009

Daniel M. Oberlin
Daniel M. Oberlin
Affiliation:
Florida State University, Tallahassee, Florida 32306
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H1(U2) be the Hardy space of the bidisc as described in (3). Each function f ∈ H1(U2) has a Taylor expansion of the form 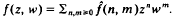. For 0<p<∞, a doubly-indexed sequence 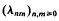is said to be a multiplier of H1(U2) into lp if

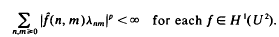
This paper is concerned with the cases p = 2 and p = 1. Theorem 1 characterises the multipliers of into l2 and is an analogue in two variables of an old result of Hardy and Littlewood. Theorem 2 characterises the sequences (an)n≥0 such that (an+m)n,m≥0 is a multiplier of H1(U) into l1

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 22 , Issue 1 , February 1979 , pp. 43 - 47
Copyright
Copyright © Edinburgh Mathematical Society 1979

References

REFERENCES

(1) Duren, P. L., Theory of Hp spaces (Academic Press, New York, 1970).Google Scholar
(2) Oberlin, D. M., The majorant problem for sequence spaces, Quart. J. Math. Oxford (2) 27 (1976), 227–240.CrossRefGoogle Scholar
(3) Rudin, W., Function theory in polydiscs (Benjamin, New York, 1969).Google Scholar
(4) Stin, E. M., Classes Hp, multiplicateurs et fonctions de Littlewood-Paley, C. R. Acad. Sci. Paris (Sér. A) 263 (1966), 780–781.Google Scholar
(5) Stein, E. M., Singular integrals and differentiability properties of functions (Princeton University Press, Princeton, N. J., 1970Google Scholar