In a given circle let the arc AP subtend an angle 3a at the centre O, it is required to trisect the angle AOP, or the arc AP.

The three trisectors will be OQ1, OQ2, OQ3, where AOQ1 = a,

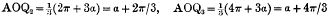
∴ Q1 Q2 Q3 form an equilateral triangle. (See Figs. 10 and 11.)

We proceed to solve the problem by drawing a conic through Q1, Q2, Q3, a nd we wish to find in what cases such a conic can be drawn, a conic cutting the circle in four points, three of which form an equilateral triangle.