Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rozenblum, G.
and
Vasilevski, N.
2016.
Toeplitz Operators Defined by Sesquilinear Forms: Bergman Space Case.
Journal of Mathematical Sciences,
Vol. 213,
Issue. 4,
p.
582.
Taskinen, Jari
and
Virtanen, Jani
2018.
On generalized Toeplitz and little Hankel operators on Bergman spaces.
Archiv der Mathematik,
Vol. 110,
Issue. 2,
p.
155.
Bonet, José
Lusky, Wolfgang
and
Taskinen, Jari
2020.
On boundedness and compactness of Toeplitz operators in weighted H∞-spaces.
Journal of Functional Analysis,
Vol. 278,
Issue. 10,
p.
108456.
Rozenblum, Grigorii Vladimirovich
and
Vasilevski, Nikolai Leonidovich
2020.
Ядерные операторы Тeплица с сингулярными символами.
Труды Математического института имени В. А. Стеклова,
Vol. 311,
Issue. ,
p.
241.
Rozenblum, Grigori V.
and
Vasilevski, Nikolai L.
2020.
Trace Class Toeplitz Operators with Singular Symbols.
Proceedings of the Steklov Institute of Mathematics,
Vol. 311,
Issue. 1,
p.
225.
Bonet, José
Lusky, Wolfgang
and
Taskinen, Jari
2021.
On the boundedness of Toeplitz operators with radial symbols over weighted sup-norm spaces of holomorphic functions.
Journal of Mathematical Analysis and Applications,
Vol. 493,
Issue. 1,
p.
124515.
Taskinen, Jari
and
Virtanen, Jani A.
2022.
Operator and Norm Inequalities and Related Topics.
p.
461.


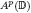 , 1 <
, 1 < 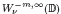 of negative order is sufficient for the boundedness of
of negative order is sufficient for the boundedness of 