Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kala, Vítězslav
and
Yatsyna, Pavlo
2021.
Lifting problem for universal quadratic forms.
Advances in Mathematics,
Vol. 377,
Issue. ,
p.
107497.
Zemková, Kristýna
2021.
Composition of binary quadratic forms over number fields.
Mathematica Slovaca,
Vol. 71,
Issue. 6,
p.
1339.
Kim, Byeong Moon
Kim, Myung-Hwan
and
Park, Dayoon
2022.
Real quadratic fields admitting universal lattices of rank 7.
Journal of Number Theory,
Vol. 233,
Issue. ,
p.
456.
Krásenský, Jakub
Raška, Martin
and
Sgallová, Ester
2022.
Pythagoras numbers of orders in biquadratic fields.
Expositiones Mathematicae,
Vol. 40,
Issue. 4,
p.
1181.
KALA, VÍTĚZSLAV
2023.
Number fields without universal quadratic forms of small rank exist in most degrees.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 174,
Issue. 2,
p.
225.
Kala, Vítězslav
and
Tinková, Magdaléna
2023.
Universal Quadratic Forms, Small Norms, and Traces in Families of Number Fields.
International Mathematics Research Notices,
Vol. 2023,
Issue. 9,
p.
7541.
Tinková, Magdaléna
2023.
Trace and norm of indecomposable integers in cubic orders.
The Ramanujan Journal,
Vol. 61,
Issue. 4,
p.
1121.
He, Zilong
Hu, Yong
and
Xu, Fei
2023.
On indefinite k-universal integral quadratic forms over number fields.
Mathematische Zeitschrift,
Vol. 304,
Issue. 1,
Kim, Daejun
and
Lee, Seok Hyeong
2024.
Lifting problem for universal quadratic forms over totally real cubic number fields.
Bulletin of the London Mathematical Society,
Vol. 56,
Issue. 3,
p.
1192.
Man, Siu Hang
2024.
Minimal rank of universal lattices and number of indecomposable elements in real multiquadratic fields.
Advances in Mathematics,
Vol. 447,
Issue. ,
p.
109694.
Gil-Muñoz, Daniel
and
Tinková, Magdaléna
2025.
Additive structure of non-monogenic simplest cubic fields.
The Ramanujan Journal,
Vol. 66,
Issue. 3,
Kala, Vítězslav
and
Man, Siu Hang
2025.
Sails for universal quadratic forms.
Selecta Mathematica,
Vol. 31,
Issue. 2,
Tinková, Magdaléna
2025.
Bounds on the Pythagoras number and indecomposables in biquadratic fields.
Proceedings of the Edinburgh Mathematical Society,
p.
1.
Kala, Vítězslav
Sgallová, Ester
and
Tinková, Magdaléna
2025.
Arithmetic of cubic number fields: Jacobi–Perron, Pythagoras, and indecomposables.
Journal of Number Theory,
Vol. 273,
Issue. ,
p.
37.
Araujo, Igor
Frederickson, Bryce
Krueger, Robert A.
Lidický, Bernard
McAllister, Tyrrell B.
Pfender, Florian
Spiro, Sam
and
Stucky, Eric Nathan
2025.
Triangle Percolation on the Grid.
Discrete & Computational Geometry,
Vol. 73,
Issue. 2,
p.
569.
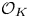 $\mathcal {O}_K$ of a totally real biquadratic field
$\mathcal {O}_K$ of a totally real biquadratic field 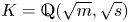 $K=\mathbb {Q}(\sqrt {m}, \sqrt {s})$. We restrict our attention to classic forms (i.e. those with all non-diagonal coefficients in
$K=\mathbb {Q}(\sqrt {m}, \sqrt {s})$. We restrict our attention to classic forms (i.e. those with all non-diagonal coefficients in 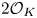 $2\mathcal {O}_K$) and prove that no such forms in three variables are universal (i.e. represent all totally positive elements of
$2\mathcal {O}_K$) and prove that no such forms in three variables are universal (i.e. represent all totally positive elements of 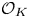 $\mathcal {O}_K$). Moreover, we show the same result for totally real number fields containing at least one non-square totally positive unit and satisfying some other mild conditions. These results provide further evidence towards Kitaoka's conjecture that there are only finitely many number fields over which such forms exist. One of our main tools are additively indecomposable elements of
$\mathcal {O}_K$). Moreover, we show the same result for totally real number fields containing at least one non-square totally positive unit and satisfying some other mild conditions. These results provide further evidence towards Kitaoka's conjecture that there are only finitely many number fields over which such forms exist. One of our main tools are additively indecomposable elements of 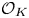 $\mathcal {O}_K$; we prove several new results about their properties.
$\mathcal {O}_K$; we prove several new results about their properties.