Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-21T23:52:52.277Z Has data issue: false hasContentIssue false
  • English
  • Français

A Theorem on the Integral of Stieltjes

Published online by Cambridge University Press:  20 January 2009

J. Hyslop
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent paper Mr J. M. Whittaker has given the following Theorem:—

If ψ (x) be the indefinite Riemann integral of a bounded positive function g(x), and if f(x) be any bounded function, then the equation

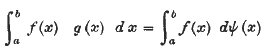
is true whenever either side exists.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 44 , February 1925 , pp. 79 - 84
Copyright
Copyright © Edinburgh Mathematical Society 1925

References

page 79 note * Proc. Lond. Math. Soc., Ser. II, Vol. 28 (1926), p. 213.

page 79 note † It is only necessary to postulate the existence of , since that of may then be deduced. [See Pollard: Quarterly Jo., Vol 49 (1923), p. 76 (II)].

page 80 note * Cf. Carlemann, : Equations Intégrales Singulièrts á Noyau Réel et Symétrique (Uppsala 1923), p. 11.Google Scholar

page 80 note † Ann. Fac. Sc. Toulouse, VIII (1894).Google Scholar

page 80 note ‡ See Hobson, : Functions of a Real Variable (Second Ed.), Vol. I, p. 506Google Scholar, sqq., along with Addendum to p. 508 in Vol. II, p. 774.

page 80 note § Quarterly Jo., Vol. 49 (1923), p. 73.Google Scholar

page 83 note † See footnote † p. 79.