Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T01:32:31.742Z Has data issue: false hasContentIssue false
  • English
  • Français

A Theorem on General Regular Transformations of Series

Published online by Cambridge University Press:  20 January 2009

Arwel Evans
Arwel Evans
Affiliation:
University of Western Ontario, London, Canada.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Many papers have been written on transformations of sequences which can be written as

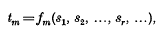
where 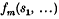is a function of a finite or infinite number of variables for fixed m. If the number of variables is finite it becomes large with m.

Almost all these papers are on linear transformations of the sr, e.g. Cesàro and Abel means, but there are obvious transformations of non-linear form which are regular, and it is a theorem on these which is considered here.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 9 , Issue 3 , July 1956 , pp. 105 - 108
Copyright
Copyright © Edinburgh Mathematical Society 1956

References

REFERENCES

[1] Leng, Sen-Ming, “A note on Cauchy's limit theorem”, American Math. Monthly, 57 (1950), 28–31.Google Scholar
[2] Hardy, G. H., Divergent Series (Oxford, 1949).Google Scholar
[3] Widder, D. V., The Laplace Transform (Princeton, 1946).Google Scholar