Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T01:48:32.850Z Has data issue: false hasContentIssue false
  • English
  • Français

Tensor structure on kC-mod and cohomology

Part of: Categories with structure Homological methods

Published online by Cambridge University Press:  05 December 2012

Fei Xu
Fei Xu*
Affiliation:
Institut für Mathematik, Universität Paderborn, Warburger Strasse 100, 33098 Paderborn, Germany ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 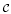be a finite category and let k be a field. We consider the category algebra 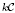and show that 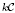-mod is closed symmetric monoidal. Through comparing 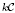with a co-commutative bialgebra, we exhibit the similarities and differences between them in terms of homological properties. In particular, we give a module-theoretic approach to the multiplicative structure of the cohomology rings of small categories. As an application, we prove that the Hochschild cohomology rings of a certain type of finite category algebras are finitely generated.

Keywords

category algebraclosed symmetric monoidal categoryordinary cohomology ringHochschild cohomology ringtransporter categoriesfinite generation

MSC classification

Secondary: 16E40: (Co)homology of rings and algebras (e.g. Hochschild, cyclic, dihedral, etc.) 18D10: Monoidal categories (= multiplicative categories), symmetric monoidal categories, braided categories
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 56 , Issue 1 , February 2013 , pp. 349 - 370
Copyright
Copyright © Edinburgh Mathematical Society 2012

References

1.Baues, H.-J. and Wirsching, G., Cohomology of small categories, J. Pure Appl. Alg. 38 (1985), 187–211.CrossRefGoogle Scholar
2.Benson, D., Representations and cohomology, I, Cambridge Studies in Advanced Mathematics, Volume 30 (Cambridge University Press, 1998).Google Scholar
3.Broto, C., Levi, R. and Oliver, B., Homotopy equivalences of p-completed classifying spaces of finite groups, Invent. Math. 151 (2003), 611–664.CrossRefGoogle Scholar
4.Broto, C., Levi, R. and Oliver, B., The homotopy theory of fusion systems, J. Am. Math. Soc. 16 (2003), 779–856.CrossRefGoogle Scholar
5.Dwyer, W. G. and Henn, H.-W., Homotopy theoretic methods in group cohomology (Birkhäuser, 2001).CrossRefGoogle Scholar
6.Etingof, P. and Ostrik, V., Finite tensor categories, Moscow Math. J. 4 (2004), 627–654, 782–783.CrossRefGoogle Scholar
7.Friedlander, E., Franjou, V., Pirashivili, T. and Schwartz, L., Functor homology theory, Panoramas et Synthéses, Volume 16 (Société de Mathématique de France, Paris, 2003).Google Scholar
8.Gabriel, P. and Zisman, M., Calculus of fractions and homotopy theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, New Series, Volume 35 (Springer, 1967).CrossRefGoogle Scholar
9.Hilton, P. and Stammbach, U., A course in homological algebra, 2nd edn, Graduate Texts in Mathematics, Volume 4 (Springer, 1997).CrossRefGoogle Scholar
10.Linckelmann, M., Varieties in block theory, J. Alg. 215 (1999), 460–480.CrossRefGoogle Scholar
11.Linckelmann, M., Fusion category algebras, J. Alg. 277 (2004), 222–235.CrossRefGoogle Scholar
12.Linckelmann, M., Hochschild and block cohomology varieties are isomorphic J. Lond. Math. Soc. 81 (2010), 389–411.CrossRefGoogle Scholar
13.Lane, S. Mac, Categories for the working mathematician, 2nd edn, Graduate Texts in Mathematics, Volume 5 (Springer, 1998).Google Scholar
14.Mitchell, B., Rings with several objects, Adv. Math. 8 (1972), 1–161.CrossRefGoogle Scholar
15.Oliver, B., Higher limits via Steinberg representations, Commun. Alg. 22 (1994), 1381–1393.CrossRefGoogle Scholar
16.Oliver, B. and Ventura, J., Extensions of linking systems with p-group kernel, Math. Annalen 338 (2007), 983–1043.CrossRefGoogle Scholar
17.Quillen, D., Higher algebraic K-theory, I, Lecture Notes in Mathematics, Volume 341, pp. 85–147 (Springer, 1973).Google Scholar
18.Siegel, S. and Witherspoon, S., The Hochschild cohomology ring of a group algebra, Proc. Lond. Math. Soc. 79 (1999), 131–157.CrossRefGoogle Scholar
19.Suarez-Alvarez, M., The Hilton-Eckmann argument for the anti-commutativity of cup product, Proc. Am. Math. Soc. 132 (2004), 2241–2246.CrossRefGoogle Scholar
20.Sweedler, M., Hopf algebras, Mathematics Lecture Notes, Volume 44 (Addison-Wesley, 1969).Google Scholar
21.Swenson, D., The Steinberg complex of an arbitrary finite group in arbitrary positive characteristic, PhD Thesis, University of Minnesota (2009).Google Scholar
22.Thévenaz, J., G-algebras and modular representation theory (Oxford University Press, 1995).Google Scholar
23.Webb, P. J., An introduction to the representations and cohomology of categories, in Group representation theory, pp. 149–173 (EPFL Press, Lausanne, 2007).Google Scholar
24.Xu, F., Representations of small categories and their applications, J. Alg. 317 (2007), 153–183.CrossRefGoogle Scholar
25.Xu, F., Hochschild and ordinary cohomology rings of small categories, Adv. Math. 219 (2008), 1872–1893.CrossRefGoogle Scholar