Published online by Cambridge University Press: 20 January 2009
R will denote a Dedekind domain and Pone of its prime ideals. A P-primary module will be an R-module all of whose non-zero elements have annihilators that are powers of the prime P. In all that follows E is such a module.
The height of 0 ≠ x ∈ E will be max{n : x ∈ PnE}. It is denoted by h(x). If this maximum does not exist we will say h(x)∞.
Clearly the condition 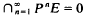 is equivalent to E having no non-zero elements of infinite height. Adopting the terminology of (2, Ch. XI) where such modules over the ring of integers are studied, we will call these modules separable and reduced.
is equivalent to E having no non-zero elements of infinite height. Adopting the terminology of (2, Ch. XI) where such modules over the ring of integers are studied, we will call these modules separable and reduced.