Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bocci, Cristiano
Cooper, Susan
Guardo, Elena
Harbourne, Brian
Janssen, Mike
Nagel, Uwe
Seceleanu, Alexandra
Tuyl, Adam Van
and
Vu, Thanh
2016.
The Waldschmidt constant for squarefree monomial ideals.
Journal of Algebraic Combinatorics,
Vol. 44,
Issue. 4,
p.
875.
Akesseh, Solomon
2017.
Ideal containments under flat extensions.
Journal of Algebra,
Vol. 492,
Issue. ,
p.
44.
Gimenez, Philippe
Martínez-Bernal, José
Simis, Aron
Villarreal, Rafael H.
and
Vivares, Carlos E.
2018.
Singularities, Algebraic Geometry, Commutative Algebra, and Related Topics.
p.
491.
Szemberg, Tomasz
and
Szpond, Justyna
2018.
Multigraded Algebra and Applications.
Vol. 238,
Issue. ,
p.
159.
Drabkin, Ben
Grifo, Eloísa
Seceleanu, Alexandra
and
Stone, Branden
2019.
Calculations involving symbolic powers.
Journal of Software for Algebra and Geometry,
Vol. 9,
Issue. 1,
p.
71.
Janssen, Mike
Kamp, Thomas
and
Vander Woude, Jason
2019.
Comparing powers of edge ideals.
Journal of Algebra and Its Applications,
Vol. 18,
Issue. 10,
p.
1950184.
Hà, Huy Tài
and
Trung, Ngo Viet
2019.
Membership Criteria and Containments of Powers of Monomial Ideals.
Acta Mathematica Vietnamica,
Vol. 44,
Issue. 1,
p.
117.
Hà, Huy Tài
Nguyen, Hop Dang
Trung, Ngo Viet
and
Trung, Tran Nam
2020.
Symbolic powers of sums of ideals.
Mathematische Zeitschrift,
Vol. 294,
Issue. 3-4,
p.
1499.
Carlini, Enrico
Tài Hà, Huy
Harbourne, Brian
and
Van Tuyl, Adam
2020.
Ideals of Powers and Powers of Ideals.
Vol. 27,
Issue. ,
p.
81.
Carlini, Enrico
Tài Hà, Huy
Harbourne, Brian
and
Van Tuyl, Adam
2020.
Ideals of Powers and Powers of Ideals.
Vol. 27,
Issue. ,
p.
137.
Bodas, Hrishikesh
Drabkin, Benjamin
Fong, Caleb
Jin, Su
Kim, Justin
Li, Wenxuan
Seceleanu, Alexandra
Tang, Tingting
and
Williams, Brendan
2021.
Consequences of the packing problem.
Journal of Algebraic Combinatorics,
Vol. 54,
Issue. 4,
p.
1095.
Ballico, Edoardo
Favacchio, Giuseppe
Guardo, Elena
and
Milazzo, Lorenzo
2021.
Steiner systems and configurations of points.
Designs, Codes and Cryptography,
Vol. 89,
Issue. 2,
p.
199.
Mandal, Mousumi
and
Kumar Pradhan, Dipak
2021.
Symbolic powers in weighted oriented graphs.
International Journal of Algebra and Computation,
Vol. 31,
Issue. 03,
p.
533.
Ballico, Edoardo
Favacchio, Giuseppe
Guardo, Elena
Milazzo, Lorenzo
and
Thomas, Abu Chackalamannil
2021.
Steiner Configurations Ideals: Containment and Colouring.
Mathematics,
Vol. 9,
Issue. 3,
p.
210.
Dung, Le Xuan
Hien, Truong Thi
Nguyen, Hop D.
and
Trung, Tran Nam
2021.
Regularity and Koszul property of symbolic powers of monomial ideals.
Mathematische Zeitschrift,
Vol. 298,
Issue. 3-4,
p.
1487.
DiPasquale, Michael
and
Drabkin, Ben
2021.
On resurgence via asymptotic resurgence.
Journal of Algebra,
Vol. 587,
Issue. ,
p.
64.
Bisui, Sankhaneel
Hà, Huy Tài
Jayanthan, A. V.
and
Thomas, Abu Chackalamannil
2021.
Resurgence numbers of fiber products of projective schemes.
Collectanea Mathematica,
Vol. 72,
Issue. 3,
p.
605.
Grifo, Eloísa
and
Seceleanu, Alexandra
2021.
Commutative Algebra.
p.
343.
Bisui, Sankhaneel
Grifo, Eloísa
Hà, Huy
and
Nguy𝑒̂̃n, Thái
2022.
Chudnovsky’s conjecture and the stable Harbourne–Huneke containment.
Transactions of the American Mathematical Society, Series B,
Vol. 9,
Issue. 12,
p.
371.
Mandal, Mousumi
and
Pradhan, Dipak Kumar
2022.
Comparing symbolic powers of edge ideals of weighted oriented graphs.
Journal of Algebraic Combinatorics,
Vol. 56,
Issue. 2,
p.
453.


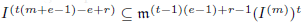 for all positive integers
for all positive integers 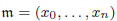 . This captures two conjectures (
. This captures two conjectures (