Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T00:51:32.884Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur l'image d'une fonction entiere de deux variables complexes

Published online by Cambridge University Press:  20 January 2009

D. Couty
D. Couty
Affiliation:
22 Rue de BéarnOdos, 65310—LaloubereFrance
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soit Θ un automorphisme analytique de 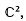, Θ ayant un point fixe attractif zo (c'está-dire il existe un voisinage V de zo tel que pour tout élément z de V, on ait 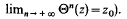Alors d'aprés un résultat bien connu, il existe une fonction F entiére de 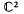dans 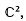, injective, telle que 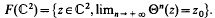Ceci provient du fait qu'il existe une fonction F, définie au voisinage de z0, telle que F'(zo)=I, vérifiant Fequation fonctionnelle 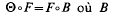est un automorphisme analytique de 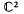vérifiant 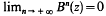pour tout z élément de .

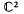Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 27 , Issue 3 , October 1984 , pp. 327 - 331
Copyright
Copyright © Edinburgh Mathematical Society 1984

References

REFERENCES

1.Bieberbach, L.Beispiel zwier ganzen Funktionen zweier komplexen Variablen, welche eine schlichte volumtreue Abbildung des R 4 auf einem Teil seiner selbst vermitten, S. B. Preuss. Akad. Wiss. (1933), 476–479.Google Scholar
2.Dixon, P. G. et al. Esterle, J. Continuity of characters on Frechet algebras and Fatou-Bieberbach functions, in preparation.Google Scholar
3.Esterle, J.Probléme de Michael et fonctions entiéres de plusieurs variables complexe, Proc. de la Conférence d'Analyse complexe de Toulouse, Mai 1982 (Springer Lect. Notes, á paraître).Google Scholar
4.Esterle, J.Mittag-Leffler methods in the theory of Banach algebras and a new approach of Michael's problem,Proceedings of the Yale conference in honour to C. E. Richart, 1983 (to appear).CrossRefGoogle Scholar
5.Fatou, P.Sur certaines fonctions uniformes de deux variables, C. R. Acad. Sci. Paris 175 (1922), 1030–1033.Google Scholar
6.Kodaira, K.Holomorphic mappings of polydiscs into compact complex manifolds, J. Differential geometry 6 (1971), 33–36.CrossRefGoogle Scholar
7.Lattes, S.Sur les formes réduites des transformations ponctuelles à deux variables, C. R. Acad. Sci. Paris 152 (1911), 1566–1569.Google Scholar
8.Nishimura, Y.Automorphismes analytiques admettant des sous-variétés de points fixés attractives dans la direction transversale, J. Math. Kyoto Univ. 23 (1983), 289–299.Google Scholar
9.Sadullaev, A.On Fatou's example, Mat. Zametki 6 (1969), 437–441.Google Scholar