No CrossRef data available.
Article contents
Sur les cordes communes à une conique et à un cercle de rayon nul
Application à la théorie géométrique des foyers dans les coniques
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Etant donnés une conique K, dont l'équation est K = 0, et un point P (α, β), l'équation générale des coniques qui passant par les points d'intersection de la conique K et du cercle P de rayon nul, qui a le point (α, β) pour centre, est
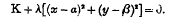
Comme les quatre points d'intersection du cercle P et de la conique K sont imaginaires, le système (1) comprend un seul couple de droites réelles Δ et Δ. Ces droites seront dites, par analogie avec une expression proposée par Chasles, les conjointes du point P et de la conique K.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1886
References
* Journal de Liouville, T. III., p. 885.Google Scholar
* La lecteur est prié de faire les figures.
* Une transformation homographiquo permet de déduire de là le théorème suivant:—Les segments d'une tangente à une conique, compris entre le point de contact de cette tangente et set intersections avec les conjointes d'un point par rapport à la conique, sont vus de ce point sous des angles égaux.
† On pout aussi remarquer, en observant que l'élément corrélatif du centre d'un cercle C est la directrice de la conique corrélative K qui correspond au foyer confondu avec le centre O de la transformation, que cette propriété est également corrélative de celle-ci:—
Toutes les normales à un cerele passent par le centre de ce cercle.
* Rouché et de Comberousse, Traité de Géométrie, T. II., 5e édit., p. 529, Ex. 916.Google Scholar
You have
Access