Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T01:51:54.822Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur les algèbres gamétiques

Published online by Cambridge University Press:  20 January 2009

Artibano Micali  and
Philippe Revoy
Artibano Micali
Affiliation:
Institut de Mathématiques, Université de Montpellier II, Place Eugène Bataillon, 34060 Montpellier, France
Philippe Revoy
Affiliation:
Institut de Mathématiques, Université de Montpellier II, Place Eugène Bataillon, 34060 Montpellier, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soient K un anneau commutatif à élémént unité, P un K-module unitaire, SK(P) l'algèbre symétrique de P et 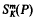le sous-K-module de SK(P) des éléments homogénes de degré m≧0. Rappelons que si P est un K-module libre de rang n + 1, l'algèbre SK(P) est isomorphe à l'algèbre des polynômes K[X0,X1,…,Xn] en les indéterminéesX0,X1,…,Xn à coefficients dans K et 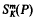est le K-module libre dont une base est formée par les monômes 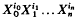tels que 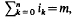ie., Par les moôomes homogènes de degré m.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 29 , Issue 2 , June 1986 , pp. 187 - 197
Copyright
Copyright © Edinburgh Mathematical Society 1986

References

BIBLIOGRAPHIE

1Bourbaki, N., Algébre I, chapitres 1 á 3 (Hermann, Paris, 1970).Google Scholar
2Gonshor, H., Special train algebra arising in genetics II, Proc. Edinburgh Math. Soc. (2) 14 (1965), 333–338.CrossRefGoogle Scholar
3Holgate, P., Genetic algebras arising in polyploidy, Proc. Edinburgh Math. Soc. (2) 15 (1966), 1–9.CrossRefGoogle Scholar
4Micali, A., Campos, T. M. M., Costa e Silva, M. C. et Ferreira, S. M. M., Dérivations dansles algébres gametiques II, Linear Algebra and its applications 64 (1985), 175–181.CrossRefGoogle Scholar
5Reiersøl, O., Genetic algebras studied recursively and by means of differential operators, Math. Scand. 10 (1962), 25–44.CrossRefGoogle Scholar