Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Inoue, Jyunji
1994.
An example of a non-exposed extreme function in the unit ball of H1.
Proceedings of the Edinburgh Mathematical Society,
Vol. 37,
Issue. 1,
p.
47.
Nakazi, Takahiko
1996.
Factorizations of outer functions and extremal problems.
Proceedings of the Edinburgh Mathematical Society,
Vol. 39,
Issue. 3,
p.
535.
Nakazi, Takahiko
2001.
Functions in N + with the positive real parts on the boundary, and extremal problems in H1.
Complex Variables, Theory and Application: An International Journal,
Vol. 44,
Issue. 4,
p.
259.


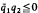 almost everywhere, and
almost everywhere, and 