Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-13T19:23:16.677Z Has data issue: false hasContentIssue false
  • English
  • Français

A stochastic proof of an extension of a theorem of Rado

Published online by Cambridge University Press:  20 January 2009

Bernt Øksendal
Bernt Øksendal
Affiliation:
Department of MathematicsUniversity of EdinburghThe King's BuildingsEdinburgh EH9 3JZ, Scotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this article is to illustrate how the theorem of Lévy about conformal invariance of Brownian motion can be used to obtain information about boundary behaviour and removable singularity sets of analytic functions. In particular, we prove a Frostman–Nevanlinna–Tsuji type result about the size of the set of asymptotic values of an analytic function at a subset of the boundary of its domain of definition (Theorem 1). Then this is used to prove the following extension of the classical Radó theorem: If φ is analytic in B\K, where B is the unit ball of ℂ;n and K is a relatively closed subset of B, and the cluster set 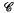of φ at K has zero harmonic measure w.r.t. φ(B\K)\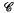≠Ø, then φ extends to a meromorphic function in B (Theorem 2).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 26 , Issue 3 , October 1983 , pp. 333 - 336
Copyright
Copyright © Edinburgh Mathematical Society 1983

References

REFERENCES

1.Aupetit, B., Une generalization du theoreme d'extension de Radó, Manuscripta Math. 23 (1978), 319–323.CrossRefGoogle Scholar
2.Bernard, A., Campbell, E. A. and Davie, A. M., Brownian motion and generalized analytic and inner functions, Ann. Inst. Fourier 29 (1979), 207–228.CrossRefGoogle Scholar
3.Cegrell, U., Generalizations of Radó's theorem, Preprint.Google Scholar
4.Cole, B. and Glicksberg, I., Jensen measures and a theorem of Radó, Journal of Funct. Anal. 35 (1980), 26–41.CrossRefGoogle Scholar
5.Csink, L. and Øksendal, B., Stochastic harmonic morphisms: Functions mapping the paths of one diffusion into the paths of another, Ann. Inst. Fourier (to appear).Google Scholar
6.Ikegami, T., Theorems of Riesz type on the boundary behaviour of harmonic maps, Osaka J. Math. 10 (1973), 247–264.Google Scholar
7.Lelong, P.Ensembles singuliers impropres des fonctions plurisousharmoniques, J. Math. Pures Appl. 36 (1957), 263–303.Google Scholar
8.Oja, K., Theorems of the Riesz type for co-fine cluster sets of harmonic morphisms, Ann. Acad. Sci. Fenn. A.I. 6 (1981), 77–88.Google Scholar
9.Osada, M., On a problem of E. L. Stout, Proc. Japan Acad. 51 (1975), 234–236.Google Scholar
10.Rado, T., Über eine nicht-fortsetzbare Riemannsche Mannigfaltigkeit, Math. Z. 20 (1924), 1–6.CrossRefGoogle Scholar
11.Stout, E. L., A generalization of a theorem of Radó, Math. Ann. 177 (1968), 339–340.CrossRefGoogle Scholar
12.Tsuji, M., Potential Theory in Modern Function Theory (Maruzen, 1959).Google Scholar