Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:54:20.826Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral mapping theorem for representations of measure algebras

Published online by Cambridge University Press:  20 January 2009

H. Seferoǧlu
H. Seferoǧlu
Affiliation:
Ondokuz Mayis University, Faculty of Arts and Sciences, Department of Mathematics, 55139, Kurupelit, Samsun, Turkey
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a locally compact abelian group, M0(G) be a closed regular subalgebra of the convolution measure algebra M(G) which contains the group algebra L1(G) and ω: M0(G) → B be a continuous homomorphism of M0(G) into the unital Banach algebra B (possibly noncommutative) such that ω(L1(G)) is without order with respect to B in the sense that if for all b ∈ B, b.ω(L1(G)) = {0} implies b = 0. We prove that if sp(ω) is a synthesis set for L1(G) then the equality 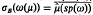holds for each μ ∈ M0(G), where sp(ω) denotes the Arveson spectrum of ω, σB(.) the usual spectrum in B, 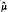the Fourier-Stieltjes transform of μ.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 40 , Issue 2 , June 1997 , pp. 261 - 266
Copyright
Copyright © Edinburgh Mathematical Society 1997

References

REFERENCES

1. D'antoni, C., Longo, R. and Zsido, L., A spectral mapping theorem for locally compact groups of operators, Pacific J. Math. 103 (1981), 17–24.Google Scholar
2. Arveson, W., On groups of automorphisms of operator algebras, J. Funct. Anal. 15 (1974), 217–243.CrossRefGoogle Scholar
3. Bourbaki, N., Theories spectrales (Hermann, 1967).Google Scholar
4. Larsen, R., An introduction to the theory of multipliers (Springer-Verlag, New York, Heidelberg, 1971).CrossRefGoogle Scholar
5. Larsen, R., Banach Algebras (Markel Dekker, Inc., New York, 1973).Google Scholar
6. Rudin, W., Fourier Analysis on Groups (Interscience, New York, 1962).Google Scholar
7. Takahasi, S.-E. and Inoue, J., A spectral mapping theorem for some representations of compact abelian groups, Proc. Edinburgh Math. Soc. 35 (1992), 47–52.CrossRefGoogle Scholar