Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-05T04:56:36.009Z Has data issue: false hasContentIssue false
  • English
  • Français

The spectral eigenmatrix problems of planar self-affine measures with four digits

Part of: Nontrigonometric harmonic analysis Classical measure theory Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  22 August 2023

Jing-Cheng Liu Open the ORCID record for Jing-Cheng Liu [Opens in a new window] ,
Min-Wei Tang Open the ORCID record for Min-Wei Tang [Opens in a new window]  and
Sha Wu Open the ORCID record for Sha Wu [Opens in a new window]
Jing-Cheng Liu
Affiliation:
Key Laboratory of Computing and Stochastic Mathematics (Ministry of Education), School of Mathematics and Statistics, Hunan Normal University, Changsha, Hunan, P.R. China ([email protected]; [email protected])
Min-Wei Tang
Affiliation:
Key Laboratory of Computing and Stochastic Mathematics (Ministry of Education), School of Mathematics and Statistics, Hunan Normal University, Changsha, Hunan, P.R. China ([email protected]; [email protected])
Sha Wu
Affiliation:
School of Mathematics, Hunan University, Changsha, Hunan, P.R. China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a Borel probability measure µ on $\mathbb{R}^n$ and a real matrix 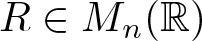$R\in M_n(\mathbb{R})$. We call R a spectral eigenmatrix of the measure µ if there exists a countable set 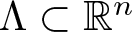$\Lambda\subset \mathbb{R}^n$ such that the sets 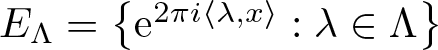$E_\Lambda=\big\{{\rm e}^{2\pi i \langle\lambda,x\rangle}:\lambda\in \Lambda\big\}$ and 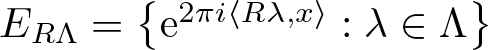$E_{R\Lambda}=\big\{{\rm e}^{2\pi i \langle R\lambda,x\rangle}:\lambda\in \Lambda\big\}$ are both orthonormal bases for the Hilbert space 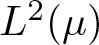$L^2(\mu)$. In this paper, we study the structure of spectral eigenmatrix of the planar self-affine measure 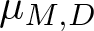$\mu_{M,D}$ generated by an expanding integer matrix 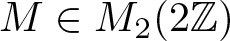$M\in M_2(2\mathbb{Z})$ and the four-elements digit set 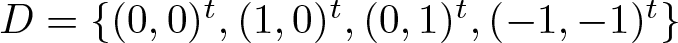$D = \{(0,0)^t,(1,0)^t,(0,1)^t,(-1,-1)^t\}$. Some sufficient and/or necessary conditions for R to be a spectral eigenmatrix of 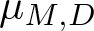$\mu_{M,D}$ are given.

Keywords

self-affine measurespectral measurespectrumspectral eigenmatrix

MSC classification

Primary: 28A25: Integration with respect to measures and other set functions 28A80: Fractals
Secondary: 42C05: Orthogonal functions and polynomials, general theory 46C05: Hilbert and pre-Hilbert spaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 3 , August 2023 , pp. 897 - 918
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

An, L. X. and He, X. G., A class of spectral Moran measures, J. Funct. Anal. 266 (1) (2014), 343–354.CrossRefGoogle Scholar
An, L. X., Dong, X. H. and He, X. G., On spectra and spectral eigenmatrix problems of the planar Sierpinski measures, Indiana Univ. Math. J. 71 (2) (2022), 913–952.CrossRefGoogle Scholar
An, L. X., He, X. G. and Tao, L., Spectrality of the planar Sierpinski family, J. Math. Anal. Appl. 432 (2) (2015), 725–732.CrossRefGoogle Scholar
Chen, M. L. and Liu, J. C., The cardinality of orthogonal exponentials of planar self-affine measures with three-element digit sets, J. Funct. Anal. 277 (1) (2019), 135–156.CrossRefGoogle Scholar
Chen, M. L., Liu, J. C. and Wang, Z. Y., Fourier bases of a class of self-affine measures. Preprint.Google Scholar
Dai, X. R., When does a Bernoulli convolution admit a spectrum?, Adv. Math. 231 (3-4) (2012), 1681–1693.CrossRefGoogle Scholar
Dai, X. R., Spectra of Cantor measures, Math. Ann. 366 (3) (2016), 1621–1647.CrossRefGoogle Scholar
Dai, X. R., Fu, X. Y. and Yan, Z. H., Spectrality of self-affine Sierpinski-type measures on $\mathbb{R}^2$, Appl. Comput. Harmon. Anal. 52 (2021), 63–81.CrossRefGoogle Scholar
Dai, X. R., He, X. G. and Lau, K. S., On spectral N-Bernoulli measures, Adv. Math. 259 (2014), 511–531.CrossRefGoogle Scholar
Deng, Q. R., On the spectra of Sierpinski-type self-affine measures, J. Funct. Anal. 270 (12) (2016), 4426–4442.CrossRefGoogle Scholar
Deng, Q. R. and Lau, K. S., Sierpinski-type spectral self-similar measures, J. Funct. Anal. 269 (5) (2015), 1310–1326.CrossRefGoogle Scholar
Deng, Q. R., He, X. G., Li, M. T. and Ye, Y. L., Spectrality of Moran-Sierpinski Measures. Preprint.Google Scholar
Dutkay, D. and Jorgensen, P., Wavelets on fractals, Rev. Mat. Iberoam. 22 (1) (2006), 131–180.CrossRefGoogle Scholar
Dutkay, D. and Jorgensen, P., Analysis of orthogonality and of orbits in affine iterated function systems, Math. Z. 256 (4) (2007), 801–823.CrossRefGoogle Scholar
Dutkay, D. and Jorgensen, P., Fourier frequencies in affine iterated function systems, J. Funct. Anal. 247 (1) (2007), 110–137.CrossRefGoogle Scholar
Dutkay, D. and Jorgensen, P., Probability and Fourier duality for affine iterated function systems, Acta Appl. Math. 107 (2009), 293–311.CrossRefGoogle Scholar
Dutkay, D. and Jorgensen, P., Fourier duality for fractal measures with affine scales, Math. Comp. 81 (280) (2012), 2253–2273.CrossRefGoogle Scholar
Dutkay, D. E. and Haussermann, J., Number theory problems from the harmonic analysis of a fractal, J. Number Theory 159 (2016), 7–26.CrossRefGoogle Scholar
Dutkay, D. E., Han, D. and Sun, Q., Divergence of the mock and scrambled Fourier series on fractal measures, Trans. Amer. Math. Soc. 366 (4) (2014), 2191–2208.CrossRefGoogle Scholar
Dutkay, D. E., Haussermann, J. and Lai, C. K., Hadamard triples generate self-affine spectral measures, Trans. Amer. Math. Soc. 371 (2) (2019), 1439–1481.CrossRefGoogle Scholar
Fu, X. Y., He, X. G. and Lau, K. S., Spectrality of self-similar tiles, Constr. Approx. 42 (3) (2015), 519–541.CrossRefGoogle Scholar
Fu, Y. S., He, X. G. and Wen, Z. X., Spectra of Bernoulli convolutions and random convolutions, J. Math. Pures Appl. 116 (2018), 105–131.CrossRefGoogle Scholar
Fuglede, B., Commuting self-adjoint partial differential operators and a group theoretic problem, J. Funct. Anal. 16 (1) (1974), 101–121.CrossRefGoogle Scholar
He, X. G., Lai, C. K. and Lau, K. S., Exponential spectra in $L^2(\mu)$, Appl. Comput. Harmon. Anal. 34 (3) (2013), 327–338.CrossRefGoogle Scholar
He, X. G., Tang, M. W. and Wu, Z. Y., Spectral structure and spectral eigenvalue problems of a class of self-similar spectral measures, J. Funct. Anal. 277 (10) (2019), 3688–3722.CrossRefGoogle Scholar
Hutchinson, J., Fractals and self-similarity, Indiana Univ. Math. J. 30 (5) (1981), 713–747.CrossRefGoogle Scholar
Jorgensen, P. and Pedersen, S., Dense analytic subspaces in fractal L 2-spaces, J. Anal. Math. 75 (1) (1998), 185–228.CrossRefGoogle Scholar
Jorgensen, P., Kornelson, K. and Shuman, K., Affine system: asymptotics at infinity for fractal measures, Acta Appl. Math. 98 (3) (2007), 181–222.CrossRefGoogle Scholar
Kolountzakis, M. N. and Matolcsi, M., Tiles with no spectra, Forum Math. 18 (3) (2006), 519–528.CrossRefGoogle Scholar
Łaba, I. and Wang, Y., On spectral Cantor measures, J. Funct. Anal. 193 (2) (2002), 409–420.CrossRefGoogle Scholar
Lagarias, J. C. and Wang, Y., Integral self-affine tiles in ${\mathbb{R}}^n$ I. Standard and nonstandard digit sets, J. Lond. Math. Soc. 54 (1) (1996), 161–179.CrossRefGoogle Scholar
Landau, H. J., Necessary density conditions for sampling and interpolation of certain entire functions, Acta Math. 117 (1967), 37–52.CrossRefGoogle Scholar
Li, J. L., Spectrality of self-affine measures on the three-dimensional Sierpinski gasket, Proc. Edinb. Math. Soc. 55 (2) (2012), 477–496.CrossRefGoogle Scholar
Li, J. L., Spectral self-affine measures on the planar Sierpinski family, Sci. China Math. 56 (08) (2013), 1619–1628.CrossRefGoogle Scholar
Li, J. L., Analysis of $\mu_M,D$-orthogonal exponentials for the planar four-element digit sets, Math. Nachr. 287 (2-3) (2014), 297–312.CrossRefGoogle Scholar
Liu, J. C., Dong, X. H. and Li, J. L., Non-spectral problem for the self-affine measures, J. Funct. Anal. 273 (2) (2017), 705–720.CrossRefGoogle Scholar
Liu, J. C., Liu, Y., Chen, M. L. and Wu, S., The cardinality of $\mu_M,D$-orthogonal exponentials for the planar four digits, Forum Math. 33 (4) (2021), 923–935.CrossRefGoogle Scholar
Liu, Y. and Wang, Y., Then uniformity of non-uniform Gabor bases, Adv. Comput. Math. 18 (2) (2003), 345–355.CrossRefGoogle Scholar
Strichartz, R., Self-similarity in harmonic analysis, J. Fourier Anal. Appl. 1 (1) (1994), 1–37.CrossRefGoogle Scholar
Strichartz, R., Mock Fourier series and transforms associated with certain Cantor measures, J. Anal. Math. 81 (1) (2000), 209–238.CrossRefGoogle Scholar
Strichartz, R., Convergence of mock Fourier series, J. Anal. Math. 99 (1) (2006), 333–353.CrossRefGoogle Scholar
Su, J., Liu, Y. and Liu, J. C., Non-spectrality of the planar self-affine measures with four-element digit sets, Fractals 27 (7) (2019), .CrossRefGoogle Scholar
Su, J., Wang, Z. Y. and Chen, M. L., Orthogonal exponential functions of the planar self-affine measures with four digits, Fractals 28 (1) (2020), .CrossRefGoogle Scholar
Tao, T., Fuglede’s conjecture is false in 5 and higher dimensions, Math. Res. Lett. 11 (2-3) (2004), 345–355.CrossRefGoogle Scholar
Wang, C. and Wu, Z. Y., On spectral eigenvalue problem of a class of self-similar spectral measures with consecutive digits, J. Fourier Anal. Appl. 26 (6) (2020), .CrossRefGoogle Scholar
Wang, Y., Wavelets, tiling, and spectral sets, Duke Math. J. 114 (1) (2002), 43–57.CrossRefGoogle Scholar