No CrossRef data available.
Article contents
Spectral Curve of the Halphen Operator
Part of:
Ordinary differential operators
Published online by Cambridge University Press: 14 November 2016
Abstract
The Halphen operator is a third-order operator of the form
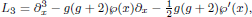
where g ≠ 2 mod(3), where the Weierstrass ℘-function satisfies the equation
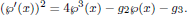
In the equianharmonic case, i.e. g2 = 0, the Halphen operator commutes with some ordinary differential operator Ln of order n ≠ 0 mod(3). In this paper we find the spectral curve of the pair L3, Ln.
MSC classification
Secondary:
34L05: General spectral theory
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 2017


