Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T01:11:54.905Z Has data issue: false hasContentIssue false
  • English
  • Français

A special sublattice of the congruence lattice of a regular semigroup

Published online by Cambridge University Press:  20 January 2009

Mario Petrich
Mario Petrich
Affiliation:
Departamento De Matemática Pura, Faculdade De Ciências, Universidade Do Porto, P. Gomes Teixeira, 4050 Porto, Portugal
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S be a regular semigroup and 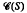be its congruence lattice. For ρ ∈ 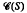, we consider the sublattice Lρ of 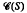generated by the congruences pw where w ∈ {K, k, T, t}* and w has no subword of the form KT, TK, kt, tk. Here K, k, T, t are the operators on 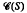induced by the kernel and the trace relations on 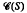. We find explicitly the least lattice L whose homomorphic image is Lρ for all ρ ∈ 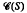and represent it as a distributive lattice in terms of generators and relations. We also consider special cases: bands of groups, E-unitary regular semigroups, completely simple semigroups, rectangular groups as well as varieties of completely regular semigroups.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 40 , Issue 3 , October 1997 , pp. 457 - 472
Copyright
Copyright © Edinburgh Mathematical Society 1997

References

REFERENCES

1.Howie, J. M., An introduction to semigroup theory (Academic Press, London, 1976).Google Scholar
2.Pastijn, F., The lattice of completely regular semigroup varieties, J. Austral. Math Soc A- 49 (1990), 24–42.CrossRefGoogle Scholar
3.Pastijn, F. and Petrich, M., Congruences on a regular semigroup, Trans. Anter. Math. Soc. 295 (1986), 607–633.CrossRefGoogle Scholar
4.Pastijn, F. and Trotter, P. G., Lattices of completely regular semigroup varieties, Pacific J. Math. 119 (1985), 191–214.CrossRefGoogle Scholar
5.Petrich, M., The kernel relation for a retract extension of Brandt semigroups, Boll. Un. Mat. Ital. B 5 (1991), 1–19.Google Scholar
6.Petrich, M., The kernel relation for certain regular semigroups, Boll. Un. Mat. Ital. B 7 (1993), 87–110.Google Scholar