Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-05T21:06:28.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Some stability properties of Arens regular bilinear operators

Published online by Cambridge University Press:  20 January 2009

A. Ülger
A. Ülger
Affiliation:
Department of MathematicsBoǧaziçi University80815 Bebek, IstanbulTurkey
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we present three results about Arens regular bilinear operators. These are: (a). Let X, Y be two Banach spaces, K a compact Hausdorff space, µ a Borel measure on K and m: X × Y →ℂ a bounded bilinear operator. Then the bilinear operator 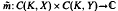defined by 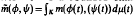is regular iff m is regular, (b) Let (Xα), (Xα),(Zα) be three families of Banach spaces and let mα:Xα ×Yα→Zα, be a family of bilinear operators with supα∥mα∥<∞. Then the bilinear operator 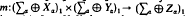defined by 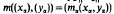is regular iff each mα, is regular, (c) Let X, Y have the Dieudonné property and let m:X × Y→Z be a bounded bilinear operator with m(X×Y) separable and such that, for each z′ in ext Z′1, z′∘m is regular. Then m is regular. Several applications of these results are also given.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 34 , Issue 3 , October 1991 , pp. 443 - 454
Copyright
Copyright © Edinburgh Mathematical Society 1991

References

REFERENCES

1.Arens, R., The adjoint of a bilinear operation, Proc. Amer. Math. Soc. 2 (1951), 839–848.CrossRefGoogle Scholar
2.Arikan, N., Arens regularity and reflexity, Quart. J. Math. Oxford Ser. (2) 32 (1981), 383–388.CrossRefGoogle Scholar
3.Civin, P. and Yood, B., The second conjugate space of a Banach algebra as an algebra, Pacific J. Math. 11 (1961), 847–870.CrossRefGoogle Scholar
4.Collins, H. S. and Ruess, W., Weak compactness in spaces of compact operators and vector-valued functions, Pacific J. Math. 106 (1983), 45–71.CrossRefGoogle Scholar
5.Delbaen, F., Weakly compact operators on disc algebra, J. Algebra 45 (1977), 284–294.CrossRefGoogle Scholar
6.Delbaen, F., The Pelczynski property for some uniform algebras, Studio Math. 64 (1979), 117–125.CrossRefGoogle Scholar
7.Diestel, J., Remarks on weak compactness in L1(µ, X), Glasgow Math. J. 18 (1977), 87–91.CrossRefGoogle Scholar
8.Diestel, J. and Uhl, J. J. Jr., Vector measures, Math. Surveys 15 (1977).Google Scholar
9.Dinculeanu, N., Vector Measures (Pergamon Press, Berlin, 1967).CrossRefGoogle Scholar
10.Duncan, J. and Hosseiniun, S. A. R., The second dual of a Banach algebra, Proc. Roy. Soc. Edinburgh 84A (1979), 309–325.CrossRefGoogle Scholar
11.Dunford, N. and Schwartz, J. T., Linear Operators, Part I (Interscience, New York, 1958).Google Scholar
12.Grothendieck, A., Sur les applications lineaires faiblement compactes d'espaces du type C(K), Canad. J. Math. 5 (1953), 129–173.CrossRefGoogle Scholar
13.Grothendieck, A., Criteres de compacité dans les espaces fonctionels généraux, Amer. J. Math. 74 (1952), 168–186.CrossRefGoogle Scholar
14.Haydon, R., Some more characterizations of Banach spaces containing l1, Math. Proc. Cambridge Philos. Soc. 80 (1976), 269–276.CrossRefGoogle Scholar
15.Kalton, N. J., Saab, E. and Saab, P., On the Dieudonné property for C(K, E), Proc. Amer. Math. Soc. 96 (1986), 50–52.Google Scholar
16.McWilliams, R. D., A note on weak sequential convergence, Pacific J. Math. 12 (1962), 333–335.CrossRefGoogle Scholar
17.Odell, E. and Rosenthal, P., A double-dual characterization of separable Banach spaces containing l1, Israel J. Math. 20 (1975), 375–384.CrossRefGoogle Scholar
18.Pelczynski, A., Banach spaces on which every unconditionally converging operator is weakly compact, Bull. Acad. Polon. Sci. 10 (1962), 641–649.Google Scholar
19.Phelps, R. P., Integral representations for elements of convex sets, in Studies in Functional Analysis (MAA Studies in Mathematics 21, edited by R. G. Bartle.Google Scholar
20.Rosenthal, H. P., A characterization of Banach spaces containing l1, Proc Nat. Acad. Sci. U.S.A. 71(1974), 2411–2413.CrossRefGoogle Scholar
21.Ruess, W. M. and Stegall, Ch.P., Extreme points in duals of operator spaces, Math. Ann. 261 (1982), 535–546.CrossRefGoogle Scholar
22.Ülcer, A., Weakly compact bilinear forms and Arens regularity, Proc. Amer. Math. Soc. 101 (1987), 697–704.Google Scholar
23.Ülcer, A., Arens regularity of the algebra K(X), Monatsh. Math. 105 (1988), 313–318.Google Scholar
24.Ülcer, A., Arens regularity of the algebra C(K, A), J. London Math. Soc. 42 (1990), 354–364.Google Scholar
25.Wojtaszcyk, P., On weakly compact operators from some uniform algebras, Studio Math. 64 (1979), 105–116.CrossRefGoogle Scholar
26.Young, N., Periodicity of functionals and representations of normed algebras on reflexive Banach spaces, Proc. Edinburgh Math. Soc. 20 (1976), 99–120.CrossRefGoogle Scholar