Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T00:50:30.728Z Has data issue: false hasContentIssue false
  • English
  • Français

Some integer-valued trigonometric sums

Published online by Cambridge University Press:  20 January 2009

Graeme J. Byrne  and
Simon J. Smith
Graeme J. Byrne
Affiliation:
Department of Mathematics, La Trobe University, Bendigo, P.O. Box 199, Bendigo, Victoria, 3552, Australia
Simon J. Smith
Affiliation:
Department of Mathematics, La Trobe University, Bendigo, P.O. Box 199, Bendigo, Victoria, 3552, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

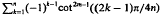It is shown that for m = 1,2,3,…, the trigonometric sums and 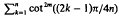can be represented as integer-valued polynomials in n of degrees 2m – 1 and 2m, respectively. Properties of these polynomials are discussed, and recurrence relations for the coefficients are obtained. The proofs of the results depend on the representations of particular polynomials of degree n – 1 or less as their own Lagrange interpolation polynomials based on the zeros of the nth Chebyshev polynomial Tn(x) = cos(narccos x), -1≤x≤1.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 40 , Issue 2 , June 1997 , pp. 393 - 401
Copyright
Copyright © Edinburgh Mathematical Society 1997

References

REFERENCES

1. Calogero, F. and Perelomov, A. M., Some Diophantine relations involving circular functions of rational angles, Linear Algebra Appl. 25 (1979), 91–94.CrossRefGoogle Scholar
2. Gradshteyn, I. S. and Ryzhik, I. M., Table of integrals, series, and products, Corrected and enlarged edition (Academic Press, New York, 1980).Google Scholar
3. Pólya, G. and Szegö, G., Problems and theorems in analysis, Volume II (Springer-Verlag, Berlin, 1976).CrossRefGoogle Scholar
4. Riesz, M., Eine trigonometrische Interpolationsformel und einige Ungleichungen für Polynome, Jahresber. Deutsch. Math. Verein. 23 (1914), 354–368.Google Scholar
5. Rivlin, Theodore J., Chebyshev polynomials: from approximation theory to algebra and number theory, Second edition (Wiley, New York, 1990).Google Scholar
6. Zygmund, A., Trigonometric series, Second edition, Volumes 1 & 2 combined (Cambridge University Press, Cambridge, 1988).Google Scholar