Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hennings, M. A.
1989.
Power-bounded elements and tauberian theorems in locally convex algebras.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 105,
Issue. 1,
p.
147.
Baskakov, A. G.
2006.
Representation theory for Banach algebras, Abelian groups, and semigroups in the spectral analysis of linear operators.
Journal of Mathematical Sciences,
Vol. 137,
Issue. 4,
p.
4885.
Baskakov, Anatoly G.
and
Krishtal, Ilya A.
2014.
Memory estimation of inverse operators.
Journal of Functional Analysis,
Vol. 267,
Issue. 8,
p.
2551.
Mustafayev, Heybetkulu
2023.
Intertwining Conditions for Two Isometries on Banach Spaces.
Complex Analysis and Operator Theory,
Vol. 17,
Issue. 8,


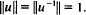
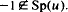 . Then there exists
. Then there exists