Article contents
Some dual aspects of the Poisson kernel
Published online by Cambridge University Press: 20 January 2009
Abstract
The Poisson kernel 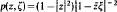 is defined for z in the open unit disc D and ζ in the unit circle ∂D. As usually employed, it is integrated with respect to the second variable and a measure on ∂D to yield a harmonic function on D. Here, we fix a σ-finite positive Borel measure m on D and integrate the Poisson kernel with respect to the first variable against a function φ in L1(m) to obtain a function Tmφ on ∂D. We ask for what measures m the range of Tm is L1(∂D), for what m the kernel of Tm is non-zero, and for what m every positive continuous function on ∂D is of the form Tmφ with φ non-negative. When m is the counting measure of a countably infinite subset {ak:k∈ℕ} of D, the function (Tmφ)(ζ) is of the form
is defined for z in the open unit disc D and ζ in the unit circle ∂D. As usually employed, it is integrated with respect to the second variable and a measure on ∂D to yield a harmonic function on D. Here, we fix a σ-finite positive Borel measure m on D and integrate the Poisson kernel with respect to the first variable against a function φ in L1(m) to obtain a function Tmφ on ∂D. We ask for what measures m the range of Tm is L1(∂D), for what m the kernel of Tm is non-zero, and for what m every positive continuous function on ∂D is of the form Tmφ with φ non-negative. When m is the counting measure of a countably infinite subset {ak:k∈ℕ} of D, the function (Tmφ)(ζ) is of the form 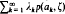 with
with 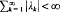 . The main results generalize results previously obtained for sums of this form. A related mapping from Lp(m) into Lp(∂D) with 1 <p<∞ is briefly considered.
. The main results generalize results previously obtained for sums of this form. A related mapping from Lp(m) into Lp(∂D) with 1 <p<∞ is briefly considered.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1990
References
REFERENCES
- 1
- Cited by


