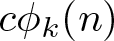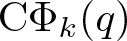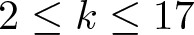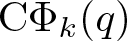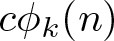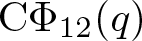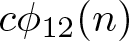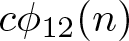1. Introduction
Throughout this paper, we always assume that q is a complex number such that ![]() $|q| \lt 1$ and adopt the following standard notation:
$|q| \lt 1$ and adopt the following standard notation:
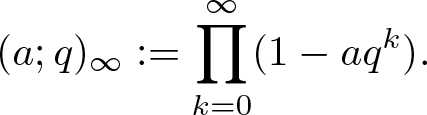 \begin{align*}
(a;q)_\infty:=\prod_{k=0}^\infty(1-aq^k).
\end{align*}
\begin{align*}
(a;q)_\infty:=\prod_{k=0}^\infty(1-aq^k).
\end{align*}In his 1984 AMS Memoir, Andrews [Reference Andrews2] defined the notion of a generalized Frobenius partition of n, which is a two-rowed array of nonnegative integers of the form:
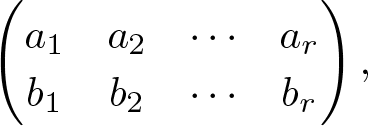 \begin{align*}
\begin{pmatrix}a_{1} &a_{2} &\cdots &a_{r}\\
b_{1} &b_{2} &\cdots &b_{r} \end{pmatrix},
\end{align*}
\begin{align*}
\begin{pmatrix}a_{1} &a_{2} &\cdots &a_{r}\\
b_{1} &b_{2} &\cdots &b_{r} \end{pmatrix},
\end{align*} wherein each row, which is of the same length, is arranged in weakly decreasing order with ![]() $n=r+\sum_{i=1}^r(a_i+b_i)$. Furthermore, Andrews studied a variant of generalized Frobenius partitions whose parts are taken from k copies of the nonnegative integers, which is called k-coloured generalized Frobenius partitions. For any
$n=r+\sum_{i=1}^r(a_i+b_i)$. Furthermore, Andrews studied a variant of generalized Frobenius partitions whose parts are taken from k copies of the nonnegative integers, which is called k-coloured generalized Frobenius partitions. For any ![]() $k\geq1$, let
$k\geq1$, let ![]() $c\phi_k(n)$ denote the number of k-coloured generalized Frobenius partitions of n. Among many other things, Andrews [Reference Andrews2, Corollary 10.1] proved that for any
$c\phi_k(n)$ denote the number of k-coloured generalized Frobenius partitions of n. Among many other things, Andrews [Reference Andrews2, Corollary 10.1] proved that for any ![]() $n\geq0$,
$n\geq0$,
From then on, many scholars extensively investigated a number of congruence properties for ![]() $c\phi_k(n)$ with different moduli. Baruah and Sarmah [Reference Baruah and Sarmah3, Reference Baruah and Sarmah4] derived some congruences modulo small powers of 2 for
$c\phi_k(n)$ with different moduli. Baruah and Sarmah [Reference Baruah and Sarmah3, Reference Baruah and Sarmah4] derived some congruences modulo small powers of 2 for ![]() $c\phi_4(n)$ and some congruences modulo small powers of 3 for
$c\phi_4(n)$ and some congruences modulo small powers of 3 for ![]() $c\phi_6(n)$. Congruence properties modulo powers of 5 for
$c\phi_6(n)$. Congruence properties modulo powers of 5 for ![]() $c\phi_3(n)$ and
$c\phi_3(n)$ and ![]() $c\phi_4(n)$ were subsequently considered by Ono [Reference Ono28], Lovejoy [Reference Lovejoy26], Xiong [Reference Xiong39], Sellers [Reference Sellers31], Xia [Reference Xia38], Hirschhorn and Sellers [Reference Hirschhorn and Sellers21], Chan, Wang and Yang [Reference Chan, Wang and Yang7], and Wang and Zhang [Reference Wang and Zhang34]. Congruence properties modulo 7 for
$c\phi_4(n)$ were subsequently considered by Ono [Reference Ono28], Lovejoy [Reference Lovejoy26], Xiong [Reference Xiong39], Sellers [Reference Sellers31], Xia [Reference Xia38], Hirschhorn and Sellers [Reference Hirschhorn and Sellers21], Chan, Wang and Yang [Reference Chan, Wang and Yang7], and Wang and Zhang [Reference Wang and Zhang34]. Congruence properties modulo 7 for ![]() $c\phi_4(n)$ were investigated by Lin [Reference Lin25] and Zhang and Wang [Reference Zhang and Wang41]. Congruence properties of
$c\phi_4(n)$ were investigated by Lin [Reference Lin25] and Zhang and Wang [Reference Zhang and Wang41]. Congruence properties of ![]() $c\phi_6(n)$ modulo powers of 3 were successively investigated by Xia [Reference Xia37], Hirschhorn [Reference Hirschhorn16], Gu, Wang and Xia [Reference Gu, Wang and Xia14] and the third author [Reference Tang32]. The third author [Reference Tang33] also established congruence properties modulo 5 for
$c\phi_6(n)$ modulo powers of 3 were successively investigated by Xia [Reference Xia37], Hirschhorn [Reference Hirschhorn16], Gu, Wang and Xia [Reference Gu, Wang and Xia14] and the third author [Reference Tang32]. The third author [Reference Tang33] also established congruence properties modulo 5 for ![]() $c\phi_8(n)$ and
$c\phi_8(n)$ and ![]() $c\phi_9(n)$. There are other studies on congruence properties for
$c\phi_9(n)$. There are other studies on congruence properties for ![]() $c\phi_k(n)$; see, for example, [Reference Cui and Gu9–Reference Garvan and Sellers13, Reference Jameson and Wieczorek22–Reference Kolitsch24, Reference Mestrige27, Reference Paule and Radu29, Reference Qu30, Reference Wang36].
$c\phi_k(n)$; see, for example, [Reference Cui and Gu9–Reference Garvan and Sellers13, Reference Jameson and Wieczorek22–Reference Kolitsch24, Reference Mestrige27, Reference Paule and Radu29, Reference Qu30, Reference Wang36].
In 2019, Chan, Wang and Yang [Reference Chan, Wang and Yang8] systematically investigated the arithmetic properties of ![]() $\textrm{C}\Phi_k(q)$ for
$\textrm{C}\Phi_k(q)$ for ![]() $2\leq k\leq17$, where
$2\leq k\leq17$, where ![]() $\textrm{C}\Phi_k(q)$ denotes the generating function of
$\textrm{C}\Phi_k(q)$ denotes the generating function of ![]() $c\phi_k(n)$. In particular, they [Reference Chan, Wang and Yang8, Equation (6.26)] proved that (some typos have been corrected)
$c\phi_k(n)$. In particular, they [Reference Chan, Wang and Yang8, Equation (6.26)] proved that (some typos have been corrected)
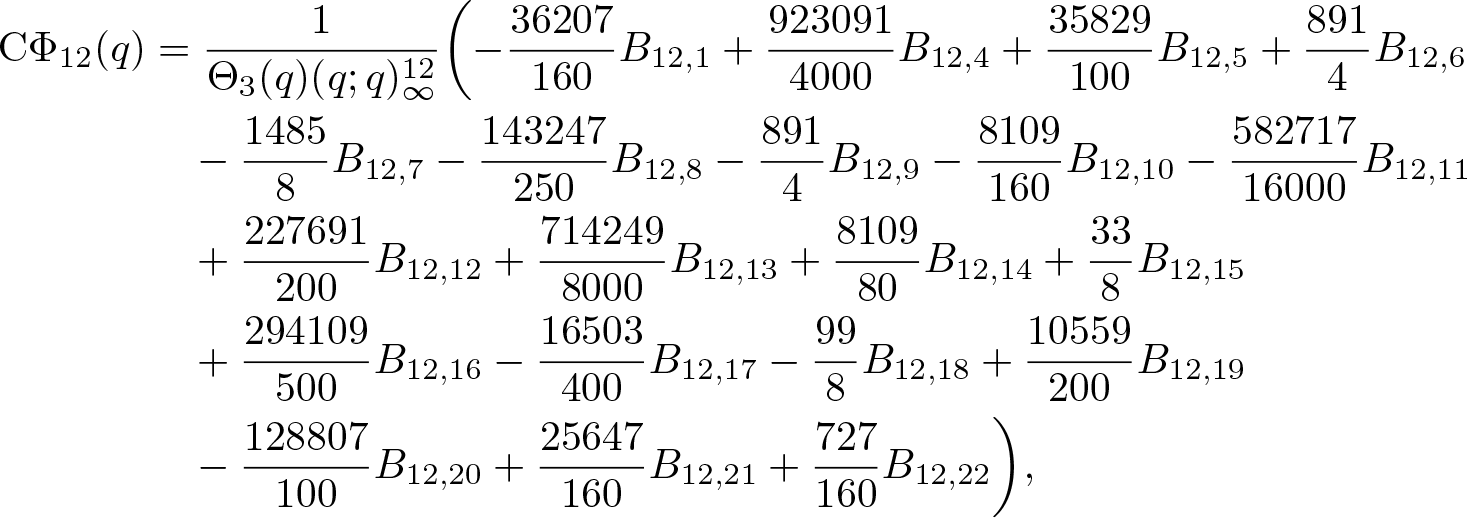 \begin{align}
\textrm{C}\Phi_{12}(q) &=\dfrac{1}{\Theta_3(q)(q;q)_\infty^{12}}
\bigg({-}\dfrac{36207}{160}B_{12,1}
+\dfrac{923091}{4000}B_{12,4}+\dfrac{35829}{100}B_{12,5}
+\dfrac{891}{4}B_{12,6}\nonumber\\
&\quad-\dfrac{1485}{8}B_{12,7}-\dfrac{143247}{250}B_{12,8}
-\dfrac{891}{4}B_{12,9}-\dfrac{8109}{160}B_{12,10}
-\dfrac{582717}{16000}B_{12,11}\nonumber\\
&\quad+\dfrac{227691}{200}B_{12,12}+\dfrac{714249}{8000}B_{12,13}
+\dfrac{8109}{80}B_{12,14}+\dfrac{33}{8}B_{12,15}\nonumber\\
&\quad+\dfrac{294109}{500}B_{12,16}-\dfrac{16503}{400}B_{12,17}
-\dfrac{99}{8}B_{12,18}+\dfrac{10559}{200}B_{12,19}\nonumber\\
&\quad-\dfrac{128807}{100}B_{12,20}+\dfrac{25647}{160}B_{12,21}
+\dfrac{727}{160}B_{12,22}\bigg),
\end{align}
\begin{align}
\textrm{C}\Phi_{12}(q) &=\dfrac{1}{\Theta_3(q)(q;q)_\infty^{12}}
\bigg({-}\dfrac{36207}{160}B_{12,1}
+\dfrac{923091}{4000}B_{12,4}+\dfrac{35829}{100}B_{12,5}
+\dfrac{891}{4}B_{12,6}\nonumber\\
&\quad-\dfrac{1485}{8}B_{12,7}-\dfrac{143247}{250}B_{12,8}
-\dfrac{891}{4}B_{12,9}-\dfrac{8109}{160}B_{12,10}
-\dfrac{582717}{16000}B_{12,11}\nonumber\\
&\quad+\dfrac{227691}{200}B_{12,12}+\dfrac{714249}{8000}B_{12,13}
+\dfrac{8109}{80}B_{12,14}+\dfrac{33}{8}B_{12,15}\nonumber\\
&\quad+\dfrac{294109}{500}B_{12,16}-\dfrac{16503}{400}B_{12,17}
-\dfrac{99}{8}B_{12,18}+\dfrac{10559}{200}B_{12,19}\nonumber\\
&\quad-\dfrac{128807}{100}B_{12,20}+\dfrac{25647}{160}B_{12,21}
+\dfrac{727}{160}B_{12,22}\bigg),
\end{align} where the ![]() $B_{12,i}$ for
$B_{12,i}$ for ![]() $i\in\{1,4,5,\ldots,22\}$ are some functions involving the following two theta functions, given by
$i\in\{1,4,5,\ldots,22\}$ are some functions involving the following two theta functions, given by
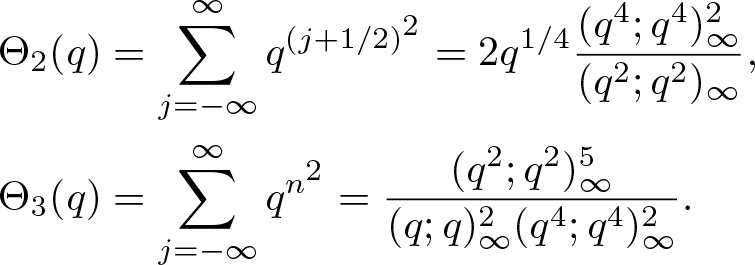 \begin{align*}
\Theta_2(q) &=\sum_{j=-\infty}^\infty q^{(j+1/2)^2}
=2q^{1/4}\dfrac{(q^4;q^4)_\infty^2}{(q^2;q^2)_\infty},\\
\Theta_3(q) &=\sum_{j=-\infty}^\infty q^{n^2}
=\dfrac{(q^2;q^2)_\infty^5}{(q;q)_\infty^2(q^4;q^4)_\infty^2}.
\end{align*}
\begin{align*}
\Theta_2(q) &=\sum_{j=-\infty}^\infty q^{(j+1/2)^2}
=2q^{1/4}\dfrac{(q^4;q^4)_\infty^2}{(q^2;q^2)_\infty},\\
\Theta_3(q) &=\sum_{j=-\infty}^\infty q^{n^2}
=\dfrac{(q^2;q^2)_\infty^5}{(q;q)_\infty^2(q^4;q^4)_\infty^2}.
\end{align*} It is easy to see that the coefficients of many terms in (1.1) are not integers. Therefore, a natural question is whether there is another expression with integral coefficients for ![]() $\textrm{C}\Phi_{12}(q)$. The first purpose of this paper is to establish the following expression for
$\textrm{C}\Phi_{12}(q)$. The first purpose of this paper is to establish the following expression for ![]() $\textrm{C}\Phi_{12}(q)$. For the sake of convenience, denote
$\textrm{C}\Phi_{12}(q)$. For the sake of convenience, denote
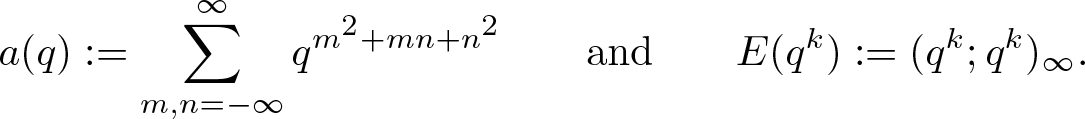 \begin{align}
a(q):=\sum_{m,n=-\infty}^\infty q^{m^2+mn+n^2}
\qquad\textrm{and}\qquad E(q^k):=(q^k;q^k)_\infty.
\end{align}
\begin{align}
a(q):=\sum_{m,n=-\infty}^\infty q^{m^2+mn+n^2}
\qquad\textrm{and}\qquad E(q^k):=(q^k;q^k)_\infty.
\end{align}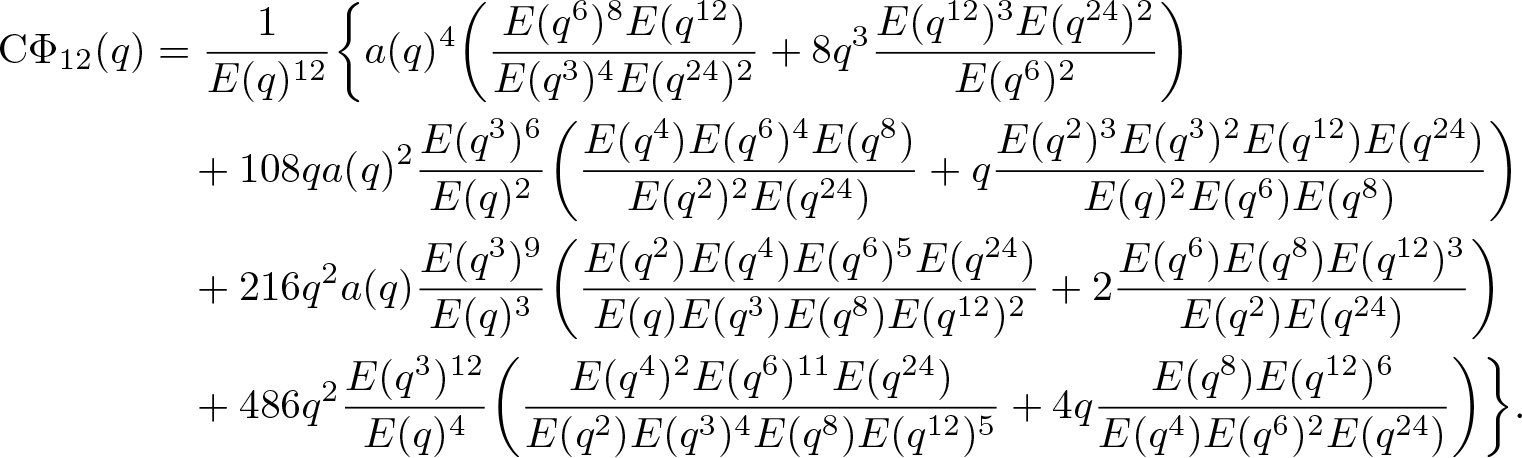 \begin{align}
\textrm{C}\Phi_{12}(q) &=\dfrac{1}{E(q)^{12}}
\bigg\{a(q)^4\bigg(\dfrac{E(q^6)^8E(q^{12})}{E(q^3)^4E(q^{24})^2}
+8q^3\dfrac{E(q^{12})^3E(q^{24})^2}{E(q^6)^2}\bigg)\nonumber\\
&\quad+108qa(q)^2\dfrac{E(q^3)^6}{E(q)^2}
\bigg(\dfrac{E(q^4)E(q^6)^4E(q^8)}{E(q^2)^2E(q^{24})}
+q\dfrac{E(q^2)^3E(q^3)^2E(q^{12})E(q^{24})}{E(q)^2E(q^6)E(q^8)}\bigg)\nonumber\\
&\quad+216q^2a(q)\dfrac{E(q^3)^9}{E(q)^3}
\bigg(\dfrac{E(q^2)E(q^4)E(q^6)^5E(q^{24})}{E(q)E(q^3)E(q^8)E(q^{12})^2}
+2\dfrac{E(q^6)E(q^8)E(q^{12})^3}{E(q^2)E(q^{24})}\bigg)\nonumber\\
&\quad+486q^2\dfrac{E(q^3)^{12}}{E(q)^4}\bigg(\dfrac{E(q^4)^2E(q^6)^{11}
E(q^{24})}{E(q^2)E(q^3)^4E(q^8)E(q^{12})^5}+4q\dfrac{E(q^8)E(q^{12})^6}
{E(q^4)E(q^6)^2E(q^{24})}\bigg)\bigg\}.
\end{align}
\begin{align}
\textrm{C}\Phi_{12}(q) &=\dfrac{1}{E(q)^{12}}
\bigg\{a(q)^4\bigg(\dfrac{E(q^6)^8E(q^{12})}{E(q^3)^4E(q^{24})^2}
+8q^3\dfrac{E(q^{12})^3E(q^{24})^2}{E(q^6)^2}\bigg)\nonumber\\
&\quad+108qa(q)^2\dfrac{E(q^3)^6}{E(q)^2}
\bigg(\dfrac{E(q^4)E(q^6)^4E(q^8)}{E(q^2)^2E(q^{24})}
+q\dfrac{E(q^2)^3E(q^3)^2E(q^{12})E(q^{24})}{E(q)^2E(q^6)E(q^8)}\bigg)\nonumber\\
&\quad+216q^2a(q)\dfrac{E(q^3)^9}{E(q)^3}
\bigg(\dfrac{E(q^2)E(q^4)E(q^6)^5E(q^{24})}{E(q)E(q^3)E(q^8)E(q^{12})^2}
+2\dfrac{E(q^6)E(q^8)E(q^{12})^3}{E(q^2)E(q^{24})}\bigg)\nonumber\\
&\quad+486q^2\dfrac{E(q^3)^{12}}{E(q)^4}\bigg(\dfrac{E(q^4)^2E(q^6)^{11}
E(q^{24})}{E(q^2)E(q^3)^4E(q^8)E(q^{12})^5}+4q\dfrac{E(q^8)E(q^{12})^6}
{E(q^4)E(q^6)^2E(q^{24})}\bigg)\bigg\}.
\end{align} By utilizing a general congruence relation [Reference Chan, Wang and Yang8, Theorem 5.3], Chan et al. [Reference Chan, Wang and Yang8, Equations (6.28) and (6.29)] derived that for any ![]() $n\geq0$,
$n\geq0$,
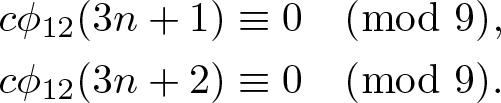 \begin{align}
c\phi_{12}(3n+1) &\equiv0\pmod{9},\nonumber\\
c\phi_{12}(3n+2) &\equiv0\pmod{9}.
\end{align}
\begin{align}
c\phi_{12}(3n+1) &\equiv0\pmod{9},\nonumber\\
c\phi_{12}(3n+2) &\equiv0\pmod{9}.
\end{align} The other purpose of this paper is to prove the following congruences modulo 27 and 81 enjoyed by ![]() $c\phi_{12}(n)$.
$c\phi_{12}(n)$.
Theorem 1.2. For any ![]() $n\geq0$,
$n\geq0$,
Remark 1.3. Obviously, (1.5) is a stronger form of (1.4). By computation, one sees that ![]() $c\phi_{12}(2)=4644\not\equiv0\pmod{81}$. From this perspective, the modulus in (1.5) is best possible. So does (1.6) and (1.7).
$c\phi_{12}(2)=4644\not\equiv0\pmod{81}$. From this perspective, the modulus in (1.5) is best possible. So does (1.6) and (1.7).
Actually, (1.5)–(1.7) appear to be just the tip of the iceberg. With the help of a computer, we pose the following three families of conjectural congruences modulo powers of 3 satisfied by ![]() $c\phi_{12}(n)$.
$c\phi_{12}(n)$.
Conjecture 1.4. For any ![]() $n\geq0$ and
$n\geq0$ and ![]() $\alpha\geq0$,
$\alpha\geq0$,
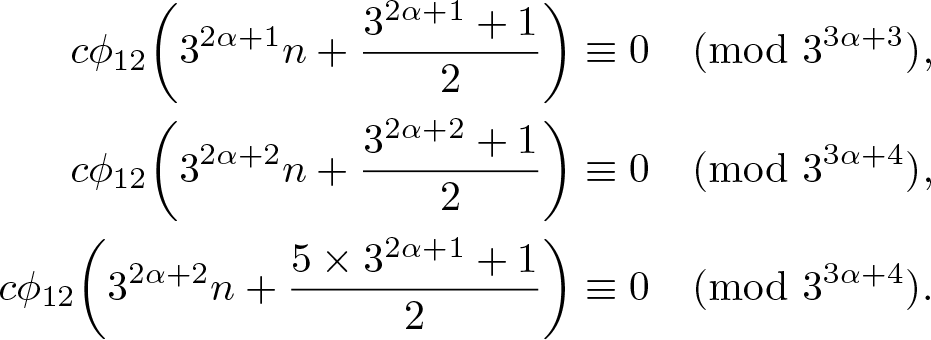 \begin{align*}
c\phi_{12}{\left(3^{2\alpha+1}n+\dfrac{3^{2\alpha+1}+1}{2}\right)}
&\equiv0\pmod{3^{3\alpha+3}},\\
c\phi_{12}{\left(3^{2\alpha+2}n+\dfrac{3^{2\alpha+2}+1}{2}\right)}
&\equiv0\pmod{3^{3\alpha+4}},\\
c\phi_{12}{\left(3^{2\alpha+2}n+\dfrac{5\times3^{2\alpha+1}+1}{2}\right)}
&\equiv0\pmod{3^{3\alpha+4}}.
\end{align*}
\begin{align*}
c\phi_{12}{\left(3^{2\alpha+1}n+\dfrac{3^{2\alpha+1}+1}{2}\right)}
&\equiv0\pmod{3^{3\alpha+3}},\\
c\phi_{12}{\left(3^{2\alpha+2}n+\dfrac{3^{2\alpha+2}+1}{2}\right)}
&\equiv0\pmod{3^{3\alpha+4}},\\
c\phi_{12}{\left(3^{2\alpha+2}n+\dfrac{5\times3^{2\alpha+1}+1}{2}\right)}
&\equiv0\pmod{3^{3\alpha+4}}.
\end{align*}The rest of this paper is organized as follows. In § 2, we collect some necessary lemmas which will be utilized to prove the main results later. The proofs of Theorems 1.1 and 1.2 are presented in § 3.
2. Some preliminary results
To prove (1.5)–(1.7), we first collect some necessary identities.
Lemma 2.1.
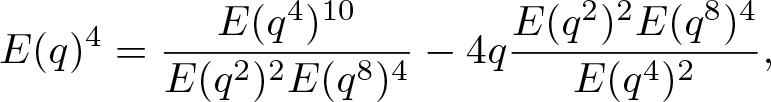 \begin{align}
E(q)^4 &=\dfrac{E(q^4)^{10}}{E(q^2)^2E(q^8)^4}
-4q\dfrac{E(q^2)^2E(q^8)^4}{E(q^4)^2},
\end{align}
\begin{align}
E(q)^4 &=\dfrac{E(q^4)^{10}}{E(q^2)^2E(q^8)^4}
-4q\dfrac{E(q^2)^2E(q^8)^4}{E(q^4)^2},
\end{align}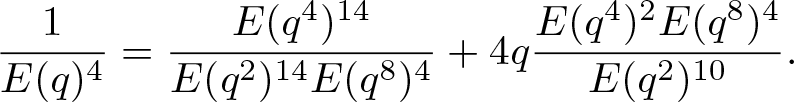 \begin{align}
\dfrac{1}{E(q)^4} &=\dfrac{E(q^4)^{14}}{E(q^2)^{14}E(q^8)^4}
+4q\dfrac{E(q^4)^2E(q^8)^4}{E(q^2)^{10}}.
\end{align}
\begin{align}
\dfrac{1}{E(q)^4} &=\dfrac{E(q^4)^{14}}{E(q^2)^{14}E(q^8)^4}
+4q\dfrac{E(q^4)^2E(q^8)^4}{E(q^2)^{10}}.
\end{align}Proof. The identities (2.1) and (2.2) are (2.9) and (2.10) in [Reference Yao and Xia40], respectively.
Lemma 2.2.
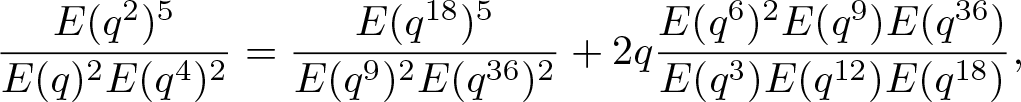 \begin{align}
\dfrac{E(q^2)^5}{E(q)^2E(q^4)^2} &=\dfrac{E(q^{18})^5}{E(q^9)^2E(q^{36})^2}
+2q\dfrac{E(q^6)^2E(q^9)E(q^{36})}{E(q^3)E(q^{12})E(q^{18})},
\end{align}
\begin{align}
\dfrac{E(q^2)^5}{E(q)^2E(q^4)^2} &=\dfrac{E(q^{18})^5}{E(q^9)^2E(q^{36})^2}
+2q\dfrac{E(q^6)^2E(q^9)E(q^{36})}{E(q^3)E(q^{12})E(q^{18})},
\end{align}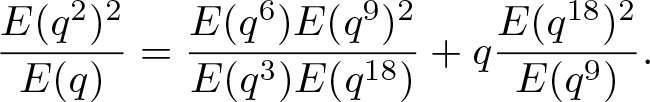 \begin{align}
\dfrac{E(q^2)^2}{E(q)} &=\dfrac{E(q^6)E(q^9)^2}{E(q^3)E(q^{18})}
+q\dfrac{E(q^{18})^2}{E(q^9)}.
\end{align}
\begin{align}
\dfrac{E(q^2)^2}{E(q)} &=\dfrac{E(q^6)E(q^9)^2}{E(q^3)E(q^{18})}
+q\dfrac{E(q^{18})^2}{E(q^9)}.
\end{align}Proof. The identities (2.3) and (2.4) follow from Corollary (i) and (ii) on page 49 of Berndt’s book [Reference Berndt5], respectively.
Lemma 2.3.
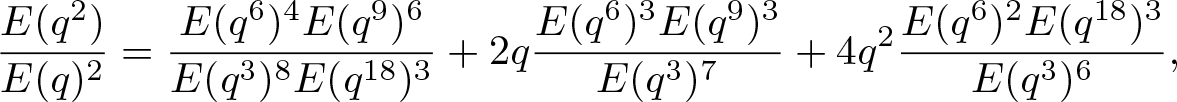 \begin{align}
\dfrac{E(q^2)}{E(q)^2} &=\dfrac{E(q^6)^4E(q^9)^6}{E(q^3)^8E(q^{18})^3}
+2q\dfrac{E(q^6)^3E(q^9)^3}{E(q^3)^7}
+4q^2\dfrac{E(q^6)^2E(q^{18})^3}{E(q^3)^6},
\end{align}
\begin{align}
\dfrac{E(q^2)}{E(q)^2} &=\dfrac{E(q^6)^4E(q^9)^6}{E(q^3)^8E(q^{18})^3}
+2q\dfrac{E(q^6)^3E(q^9)^3}{E(q^3)^7}
+4q^2\dfrac{E(q^6)^2E(q^{18})^3}{E(q^3)^6},
\end{align}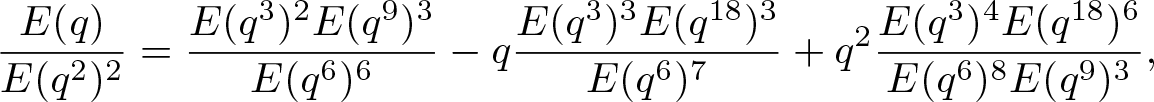 \begin{align}
\dfrac{E(q)}{E(q^2)^2} &=\dfrac{E(q^3)^2E(q^9)^3}{E(q^6)^6}
-q\dfrac{E(q^3)^3E(q^{18})^3}{E(q^6)^7}
+q^2\dfrac{E(q^3)^4E(q^{18})^6}{E(q^6)^8E(q^9)^3},
\end{align}
\begin{align}
\dfrac{E(q)}{E(q^2)^2} &=\dfrac{E(q^3)^2E(q^9)^3}{E(q^6)^6}
-q\dfrac{E(q^3)^3E(q^{18})^3}{E(q^6)^7}
+q^2\dfrac{E(q^3)^4E(q^{18})^6}{E(q^6)^8E(q^9)^3},
\end{align}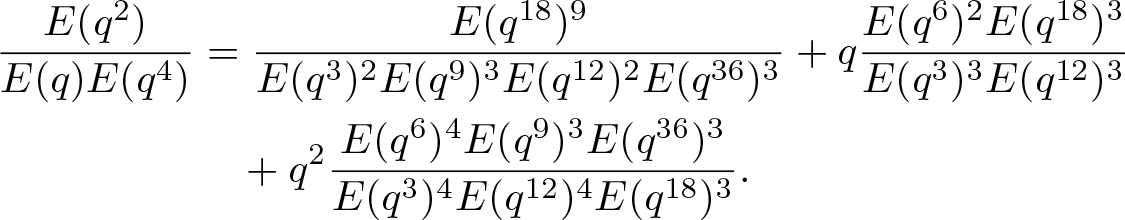 \begin{align}
\dfrac{E(q^2)}{E(q)E(q^4)}
&=\dfrac{E(q^{18})^9}{E(q^3)^2E(q^9)^3E(q^{12})^2E(q^{36})^3}
+q\dfrac{E(q^6)^2E(q^{18})^3}{E(q^3)^3E(q^{12})^3}\nonumber\\
&\quad+q^2\dfrac{E(q^6)^4E(q^9)^3E(q^{36})^3}
{E(q^3)^4E(q^{12})^4E(q^{18})^3}.
\end{align}
\begin{align}
\dfrac{E(q^2)}{E(q)E(q^4)}
&=\dfrac{E(q^{18})^9}{E(q^3)^2E(q^9)^3E(q^{12})^2E(q^{36})^3}
+q\dfrac{E(q^6)^2E(q^{18})^3}{E(q^3)^3E(q^{12})^3}\nonumber\\
&\quad+q^2\dfrac{E(q^6)^4E(q^9)^3E(q^{36})^3}
{E(q^3)^4E(q^{12})^4E(q^{18})^3}.
\end{align}Proof. The identity (2.5) was derived by Hirschhorn and Sellers [Reference Hirschhorn and Sellers19, Theorem 1.1]. The identity (2.6) is equivalent to Lemma 2.2 due to Hirschhorn and Sellers [Reference Hirschhorn and Sellers20]. Moreover, replacing q by −q in (2.6) and utilizing the fact
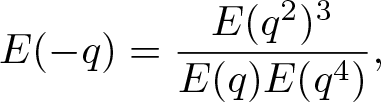 \begin{align*}
E(-q)=\dfrac{E(q^2)^3}{E(q)E(q^4)},
\end{align*}
\begin{align*}
E(-q)=\dfrac{E(q^2)^3}{E(q)E(q^4)},
\end{align*}upon simplification, we obtain (2.7).
Lemma 2.4. If a(q) is defined by (1.2), then
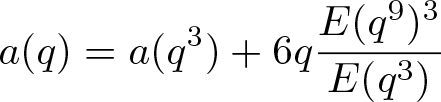 \begin{align}
a(q)=a(q^3)+6q\dfrac{E(q^9)^3}{E(q^3)}
\end{align}
\begin{align}
a(q)=a(q^3)+6q\dfrac{E(q^9)^3}{E(q^3)}
\end{align}and
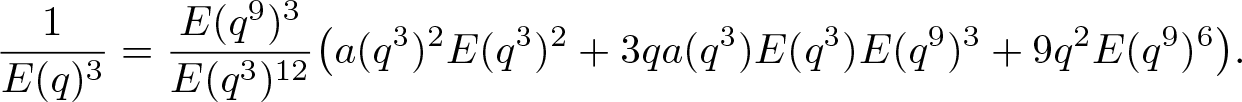 \begin{align}
\dfrac{1}{E(q)^3}=\dfrac{E(q^9)^3}{E(q^3)^{12}}
\big(a(q^3)^2E(q^3)^2+3qa(q^3)E(q^3)E(q^9)^3+9q^2E(q^9)^6\big).
\end{align}
\begin{align}
\dfrac{1}{E(q)^3}=\dfrac{E(q^9)^3}{E(q^3)^{12}}
\big(a(q^3)^2E(q^3)^2+3qa(q^3)E(q^3)E(q^9)^3+9q^2E(q^9)^6\big).
\end{align}Proof. The identity (2.8) was established by Hirschhorn, Garvan and Borwein [Reference Hirschhorn, Garvan and Borwein18, Equation (1.3)]. The identity (2.9) was proved by Wang [Reference Wang35, Equation (2.28)].
Hirschhorn et al. [Reference Hirschhorn, Garvan and Borwein18, Equation (1.5)] also proved that
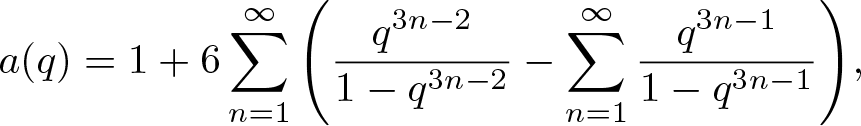 \begin{align*}
a(q)=1+6\sum_{n=1}^\infty{\left(\dfrac{q^{3n-2}}{1-q^{3n-2}}
-\sum_{n=1}^\infty\dfrac{q^{3n-1}}{1-q^{3n-1}}\right)},
\end{align*}
\begin{align*}
a(q)=1+6\sum_{n=1}^\infty{\left(\dfrac{q^{3n-2}}{1-q^{3n-2}}
-\sum_{n=1}^\infty\dfrac{q^{3n-1}}{1-q^{3n-1}}\right)},
\end{align*}from which we find that
According to the binomial theorem, one can easily establish the following congruence, which will be used frequently in the sequel.
Lemma 2.5. For any ![]() $k\geq1$,
$k\geq1$,
3. Proofs of the main results
To prove Theorem 1.1, we require the following two related lemmas.
Lemma 3.1.
 \begin{align}
\sum^{\infty}_{r_1,r_2,r_3=-\infty} &\,
q^{3\sum_{i=1}^3 r^2_i+3\sum_{1\leq i \lt j\leq3}r_ir_j}
=\dfrac{E(q^6)^8E(q^{12})}{E(q^3)^4E(q^{24})^2}
+8q^3\dfrac{E(q^{12})^3E(q^{24})^2}{E(q^6)^2},
\end{align}
\begin{align}
\sum^{\infty}_{r_1,r_2,r_3=-\infty} &\,
q^{3\sum_{i=1}^3 r^2_i+3\sum_{1\leq i \lt j\leq3}r_ir_j}
=\dfrac{E(q^6)^8E(q^{12})}{E(q^3)^4E(q^{24})^2}
+8q^3\dfrac{E(q^{12})^3E(q^{24})^2}{E(q^6)^2},
\end{align}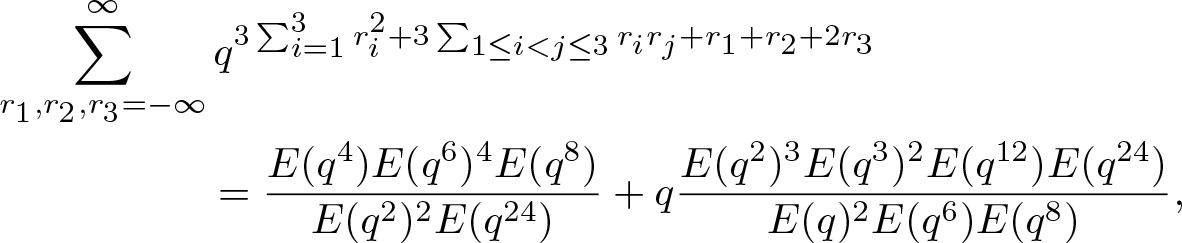 \begin{align}
\sum^{\infty}_{r_1,r_2,r_3=-\infty} &\,q^{3\sum_{i=1}^3 r^2_i
+3\sum_{1\leq i \lt j\leq3}r_ir_j+r_1+r_2+2r_3}\nonumber\\
&=\dfrac{E(q^4)E(q^6)^4E(q^8)}{E(q^2)^2E(q^{24})}
+q\dfrac{E(q^2)^3E(q^3)^2E(q^{12})E(q^{24})}
{E(q)^2E(q^6)E(q^8)},
\end{align}
\begin{align}
\sum^{\infty}_{r_1,r_2,r_3=-\infty} &\,q^{3\sum_{i=1}^3 r^2_i
+3\sum_{1\leq i \lt j\leq3}r_ir_j+r_1+r_2+2r_3}\nonumber\\
&=\dfrac{E(q^4)E(q^6)^4E(q^8)}{E(q^2)^2E(q^{24})}
+q\dfrac{E(q^2)^3E(q^3)^2E(q^{12})E(q^{24})}
{E(q)^2E(q^6)E(q^8)},
\end{align}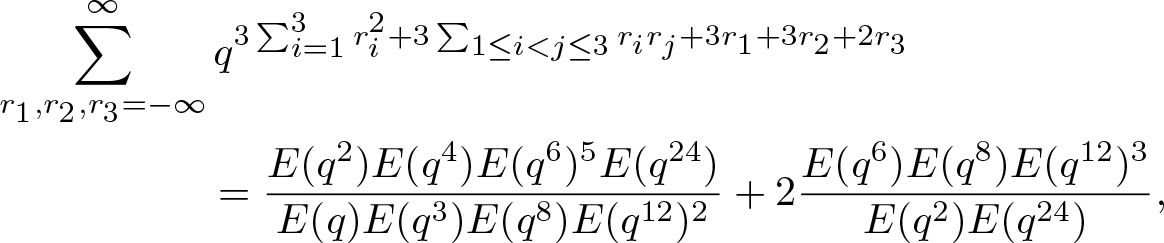 \begin{align}
\sum^{\infty}_{r_1,r_2,r_3=-\infty} &\,
q^{3\sum_{i=1}^3 r^2_i+3\sum_{1\leq i \lt j\leq3}r_ir_j+3r_1+3r_2+2r_3}\nonumber\\
&=\dfrac{E(q^2)E(q^4)E(q^6)^5E(q^{24})}{E(q)E(q^3)E(q^8)E(q^{12})^2}
+2\dfrac{E(q^6)E(q^8)E(q^{12})^3}{E(q^2)E(q^{24})},
\end{align}
\begin{align}
\sum^{\infty}_{r_1,r_2,r_3=-\infty} &\,
q^{3\sum_{i=1}^3 r^2_i+3\sum_{1\leq i \lt j\leq3}r_ir_j+3r_1+3r_2+2r_3}\nonumber\\
&=\dfrac{E(q^2)E(q^4)E(q^6)^5E(q^{24})}{E(q)E(q^3)E(q^8)E(q^{12})^2}
+2\dfrac{E(q^6)E(q^8)E(q^{12})^3}{E(q^2)E(q^{24})},
\end{align}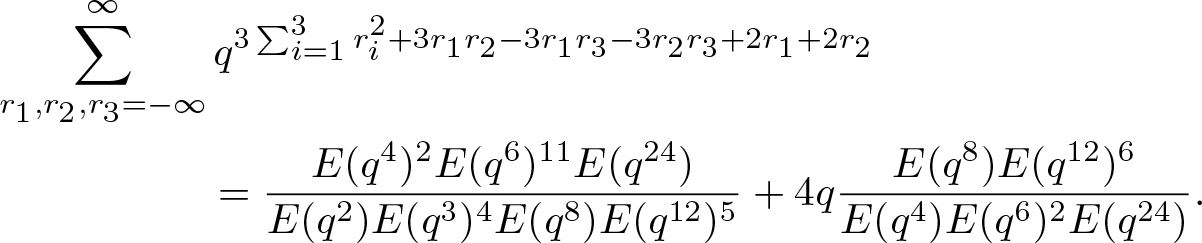 \begin{align}
\sum^{\infty}_{r_1,r_2,r_3=-\infty} &\,
q^{3\sum_{i=1}^3r_i^2+3r_1r_2-3r_1r_3-3r_2r_3+2r_1+2r_2}\nonumber\\
&=\dfrac{E(q^4)^2E(q^6)^{11}E(q^{24})}
{E(q^2)E(q^3)^4E(q^8)E(q^{12})^5}
+4q\dfrac{E(q^8)E(q^{12})^6}{E(q^4)E(q^6)^2E(q^{24})}.
\end{align}
\begin{align}
\sum^{\infty}_{r_1,r_2,r_3=-\infty} &\,
q^{3\sum_{i=1}^3r_i^2+3r_1r_2-3r_1r_3-3r_2r_3+2r_1+2r_2}\nonumber\\
&=\dfrac{E(q^4)^2E(q^6)^{11}E(q^{24})}
{E(q^2)E(q^3)^4E(q^8)E(q^{12})^5}
+4q\dfrac{E(q^8)E(q^{12})^6}{E(q^4)E(q^6)^2E(q^{24})}.
\end{align}Proof. The main ingredient in proofs of (3.1)–(3.4) is the integer matrix exact covering systems, developed by Cao [Reference Cao6]. Similar treatments were used for deriving the generating functions of four- and six-coloured generalized Frobenius partitions; see [Reference Baruah and Sarmah3, Reference Baruah and Sarmah4] for a detailed account of such applications.
We only present the proof of (3.1), and the remaining cases can be demonstrated in a similar manner.
First, we adopt the matrix
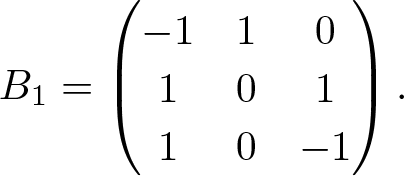 \begin{align*}
B_1=\begin{pmatrix}
-1 &1 &0\\
1 &0 &1\\
1 &0 &-1\\
\end{pmatrix}.
\end{align*}
\begin{align*}
B_1=\begin{pmatrix}
-1 &1 &0\\
1 &0 &1\\
1 &0 &-1\\
\end{pmatrix}.
\end{align*} Then, the congruences ![]() $B_1\mathbf{r}\equiv0\pmod2$ satisfy that
$B_1\mathbf{r}\equiv0\pmod2$ satisfy that
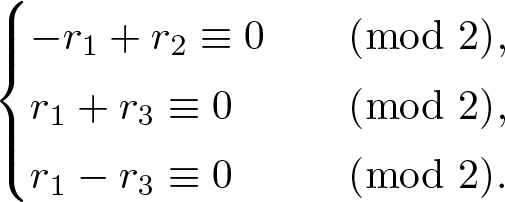 \begin{align*}
\begin{cases}
-r_1+r_2\equiv0 &\pmod2,\\
r_1+r_3\equiv0 &\pmod2,\\
r_1-r_3\equiv0 &\pmod2.
\end{cases}
\end{align*}
\begin{align*}
\begin{cases}
-r_1+r_2\equiv0 &\pmod2,\\
r_1+r_3\equiv0 &\pmod2,\\
r_1-r_3\equiv0 &\pmod2.
\end{cases}
\end{align*} Then, the above congruences contain two solutions. Namely,  $
\begin{pmatrix}
0 \\
0 \\
0\\
\end{pmatrix}
$ and
$
\begin{pmatrix}
0 \\
0 \\
0\\
\end{pmatrix}
$ and  $
\begin{pmatrix}
1 \\
1 \\
1\\
\end{pmatrix}
$ modulo 2. Therefore, we get the following integer matrix exact covering systems
$
\begin{pmatrix}
1 \\
1 \\
1\\
\end{pmatrix}
$ modulo 2. Therefore, we get the following integer matrix exact covering systems
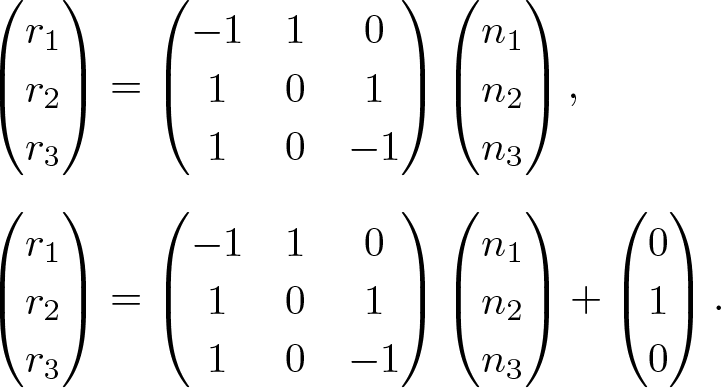 \begin{align*}
\begin{pmatrix}
r_1 \\
r_2 \\
r_3\\
\end{pmatrix}&=\begin{pmatrix}
-1 &1 &0\\
1 &0 &1\\
1 &0 &-1\\
\end{pmatrix}\begin{pmatrix}
n_1 \\
n_2 \\
n_3\\
\end{pmatrix},\\[5pt]
\begin{pmatrix}
r_1 \\
r_2 \\
r_3\\
\end{pmatrix}&=\begin{pmatrix}
-1 &1 &0\\
1 &0 &1\\
1 &0 &-1\\
\end{pmatrix}\begin{pmatrix}
n_1 \\
n_2 \\
n_3\\
\end{pmatrix}+\begin{pmatrix}
0 \\
1 \\
0\\
\end{pmatrix}.
\end{align*}
\begin{align*}
\begin{pmatrix}
r_1 \\
r_2 \\
r_3\\
\end{pmatrix}&=\begin{pmatrix}
-1 &1 &0\\
1 &0 &1\\
1 &0 &-1\\
\end{pmatrix}\begin{pmatrix}
n_1 \\
n_2 \\
n_3\\
\end{pmatrix},\\[5pt]
\begin{pmatrix}
r_1 \\
r_2 \\
r_3\\
\end{pmatrix}&=\begin{pmatrix}
-1 &1 &0\\
1 &0 &1\\
1 &0 &-1\\
\end{pmatrix}\begin{pmatrix}
n_1 \\
n_2 \\
n_3\\
\end{pmatrix}+\begin{pmatrix}
0 \\
1 \\
0\\
\end{pmatrix}.
\end{align*}Using the above integer matrix exact covering systems, we obtain that
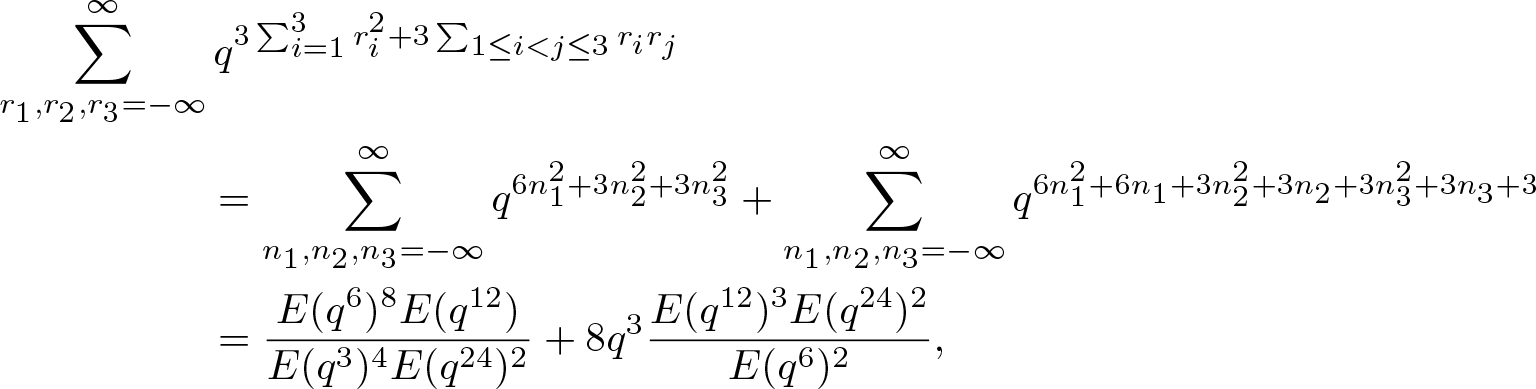 \begin{align*}
\sum^{\infty}_{r_1,r_2,r_3=-\infty} &\,
q^{3\sum_{i=1}^3 r^2_i+3\sum_{1\leq i \lt j\leq3}r_ir_j}\\
&=\sum^{\infty}_{n_1,n_2,n_3=-\infty}q^{6n^2_1+3n^2_2+3n^2_3}
+\sum^{\infty}_{n_1,n_2,n_3=-\infty}q^{6n^2_1+6n_1+3n^2_2+3n_2+3n^2_3+3n_3+3}\\
&=\dfrac{E(q^6)^8E(q^{12})}{E(q^3)^4E(q^{24})^2}
+8q^3\dfrac{E(q^{12})^3E(q^{24})^2}{E(q^6)^2},
\end{align*}
\begin{align*}
\sum^{\infty}_{r_1,r_2,r_3=-\infty} &\,
q^{3\sum_{i=1}^3 r^2_i+3\sum_{1\leq i \lt j\leq3}r_ir_j}\\
&=\sum^{\infty}_{n_1,n_2,n_3=-\infty}q^{6n^2_1+3n^2_2+3n^2_3}
+\sum^{\infty}_{n_1,n_2,n_3=-\infty}q^{6n^2_1+6n_1+3n^2_2+3n_2+3n^2_3+3n_3+3}\\
&=\dfrac{E(q^6)^8E(q^{12})}{E(q^3)^4E(q^{24})^2}
+8q^3\dfrac{E(q^{12})^3E(q^{24})^2}{E(q^6)^2},
\end{align*}which is nothing but (3.1). For (3.2) and (3.3), we also adopt the matrix B 1 and utilizing a similar strategy. However, for (3.4), we need the following matrix
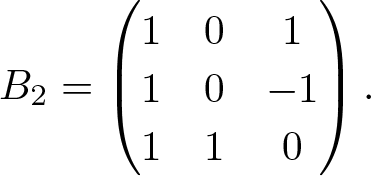 \begin{align*}
B_2=\begin{pmatrix}
1 &0 &1\\
1 &0 &-1\\
1 &1 &0\\
\end{pmatrix}.
\end{align*}
\begin{align*}
B_2=\begin{pmatrix}
1 &0 &1\\
1 &0 &-1\\
1 &1 &0\\
\end{pmatrix}.
\end{align*}This completes the proof of Lemma 3.1.
Lemma 3.2. The constant term of  ${\left(\sum^{\infty}_{r=-\infty}a^rq^{r^2}\right)}^{12}$ is
${\left(\sum^{\infty}_{r=-\infty}a^rq^{r^2}\right)}^{12}$ is
 \begin{align}
&\textrm{CT}_a{\left(\left(\sum^{\infty}_{r=-\infty}
a^rq^{r^2}\right)^{12}\right)}\nonumber\\
&\quad=a(q^2)^4\sum^{\infty}_{r_1,r_2,r_3=-\infty}
q^{6\sum_{i=1}^3 r^2_i+6\sum_{1\leq i \lt j\leq3}r_ir_j}\nonumber\\
&\qquad+108qa(q^2)^2\dfrac{E(q^6)^6}{E(q^2)^2}
\sum_{r_1,r_2,r_3=-\infty}^{\infty}q^{6\sum_{i=1}^3 r^2_i
+6\sum_{1\leq i \lt j\leq3}r_ir_j+2r_1+2r_2+4r_3}\nonumber\\
&\qquad+216q^4a(q^2)\dfrac{E(q^6)^9}{E(q^3)^3}
\sum^{\infty}_{r_1,r_2,r_3=-\infty}q^{6\sum_{i=1}^3r^2_i
+6\sum_{1\leq i \lt j\leq3}r_ir_j+6r_1+6r_2+4r_3}\nonumber\\
&\qquad+486q^4\dfrac{E(q^6)^{12}}{E(q^2)^4}
\sum^{\infty}_{r_1,r_2,r_3=-\infty}q^{6\sum_{i=1}^3 r^2_i
+6r_1r_2-6r_1r_3-6r_2r_3+4r_1+4r_2}.
\end{align}
\begin{align}
&\textrm{CT}_a{\left(\left(\sum^{\infty}_{r=-\infty}
a^rq^{r^2}\right)^{12}\right)}\nonumber\\
&\quad=a(q^2)^4\sum^{\infty}_{r_1,r_2,r_3=-\infty}
q^{6\sum_{i=1}^3 r^2_i+6\sum_{1\leq i \lt j\leq3}r_ir_j}\nonumber\\
&\qquad+108qa(q^2)^2\dfrac{E(q^6)^6}{E(q^2)^2}
\sum_{r_1,r_2,r_3=-\infty}^{\infty}q^{6\sum_{i=1}^3 r^2_i
+6\sum_{1\leq i \lt j\leq3}r_ir_j+2r_1+2r_2+4r_3}\nonumber\\
&\qquad+216q^4a(q^2)\dfrac{E(q^6)^9}{E(q^3)^3}
\sum^{\infty}_{r_1,r_2,r_3=-\infty}q^{6\sum_{i=1}^3r^2_i
+6\sum_{1\leq i \lt j\leq3}r_ir_j+6r_1+6r_2+4r_3}\nonumber\\
&\qquad+486q^4\dfrac{E(q^6)^{12}}{E(q^2)^4}
\sum^{\infty}_{r_1,r_2,r_3=-\infty}q^{6\sum_{i=1}^3 r^2_i
+6r_1r_2-6r_1r_3-6r_2r_3+4r_1+4r_2}.
\end{align}Proof. Hirschhorn [Reference Hirschhorn15] proved the following identity
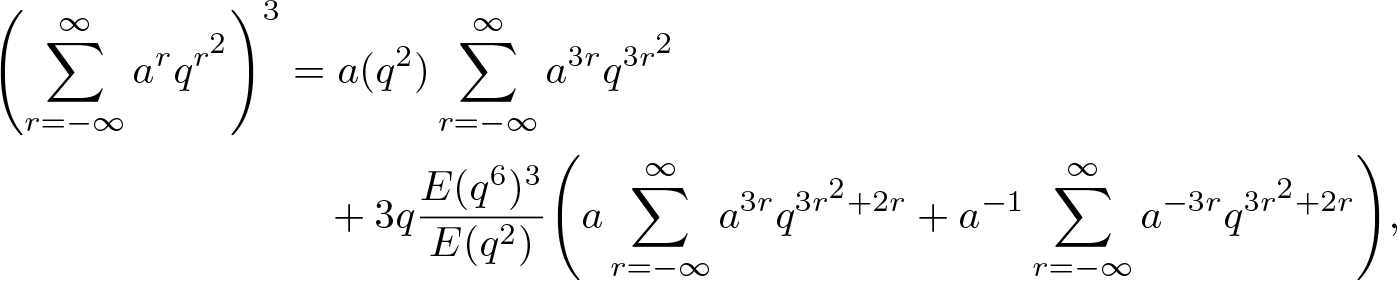 \begin{align}
{\left(\sum^{\infty}_{r=-\infty}a^rq^{r^2}\right)}^3
&=a(q^2)\sum^{\infty}_{r=-\infty}a^{3r}q^{3r^2}\nonumber\\
&\quad+3q\frac{E(q^6)^3}{E(q^2)}
{\left(a\sum^{\infty}_{r=-\infty}a^{3r}q^{3r^2+2r}
+a^{-1}\sum^{\infty}_{r=-\infty}a^{-3r}q^{3r^2+2r}\right)},
\end{align}
\begin{align}
{\left(\sum^{\infty}_{r=-\infty}a^rq^{r^2}\right)}^3
&=a(q^2)\sum^{\infty}_{r=-\infty}a^{3r}q^{3r^2}\nonumber\\
&\quad+3q\frac{E(q^6)^3}{E(q^2)}
{\left(a\sum^{\infty}_{r=-\infty}a^{3r}q^{3r^2+2r}
+a^{-1}\sum^{\infty}_{r=-\infty}a^{-3r}q^{3r^2+2r}\right)},
\end{align}where a(q) is defined as in (1.2). With the help of (3.6), we obtain that
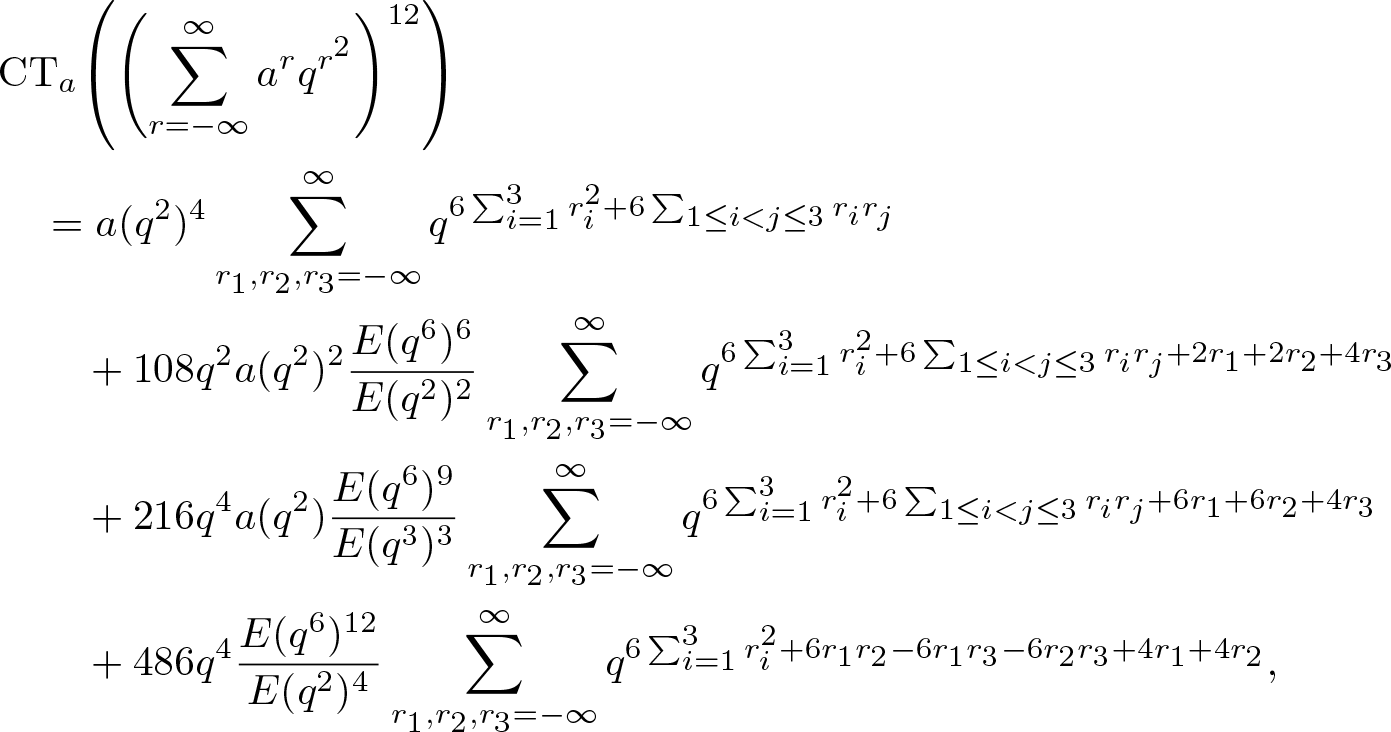 \begin{align*}
&\textrm{CT}_a{\left(\left(\sum^{\infty}_{r=-\infty}
a^rq^{r^2}\right)^{12}\right)}\\
&\quad=a(q^2)^4\sum^{\infty}_{r_1,r_2,r_3=-\infty}
q^{6\sum_{i=1}^3 r^2_i+6\sum_{1\leq i \lt j\leq3} r_ir_j}\\
&\qquad+108q^2a(q^2)^2\frac{E(q^6)^6}{E(q^2)^2}
\sum^{\infty}_{r_1,r_2,r_3=-\infty}
q^{6\sum_{i=1}^3r^2_i+6\sum_{1\leq i \lt j\leq3} r_ir_j+2r_1+2r_2+4r_3}\\
&\qquad+216q^4a(q^2)\dfrac{E(q^6)^9}{E(q^3)^3}\sum^{\infty}_{r_1,r_2,r_3=-\infty}
q^{6\sum_{i=1}^3 r^2_i+6\sum_{1\leq i \lt j\leq3} r_ir_j+6r_1+6r_2+4r_3}\\
&\qquad+486q^4\dfrac{E(q^6)^{12}}{E(q^2)^4}\sum^{\infty}_{r_1,r_2,r_3=-\infty}
q^{6\sum_{i=1}^3r^2_i+6r_1r_2-6r_1r_3-6r_2r_3+4r_1+4r_2},
\end{align*}
\begin{align*}
&\textrm{CT}_a{\left(\left(\sum^{\infty}_{r=-\infty}
a^rq^{r^2}\right)^{12}\right)}\\
&\quad=a(q^2)^4\sum^{\infty}_{r_1,r_2,r_3=-\infty}
q^{6\sum_{i=1}^3 r^2_i+6\sum_{1\leq i \lt j\leq3} r_ir_j}\\
&\qquad+108q^2a(q^2)^2\frac{E(q^6)^6}{E(q^2)^2}
\sum^{\infty}_{r_1,r_2,r_3=-\infty}
q^{6\sum_{i=1}^3r^2_i+6\sum_{1\leq i \lt j\leq3} r_ir_j+2r_1+2r_2+4r_3}\\
&\qquad+216q^4a(q^2)\dfrac{E(q^6)^9}{E(q^3)^3}\sum^{\infty}_{r_1,r_2,r_3=-\infty}
q^{6\sum_{i=1}^3 r^2_i+6\sum_{1\leq i \lt j\leq3} r_ir_j+6r_1+6r_2+4r_3}\\
&\qquad+486q^4\dfrac{E(q^6)^{12}}{E(q^2)^4}\sum^{\infty}_{r_1,r_2,r_3=-\infty}
q^{6\sum_{i=1}^3r^2_i+6r_1r_2-6r_1r_3-6r_2r_3+4r_1+4r_2},
\end{align*}which is nothing but (3.5).
We therefore complete the proof of Lemma 3.2.
Now, it is time to prove Theorem 1.1.
Proof of Theorem 1.1
In view of (3.5), we deduce that
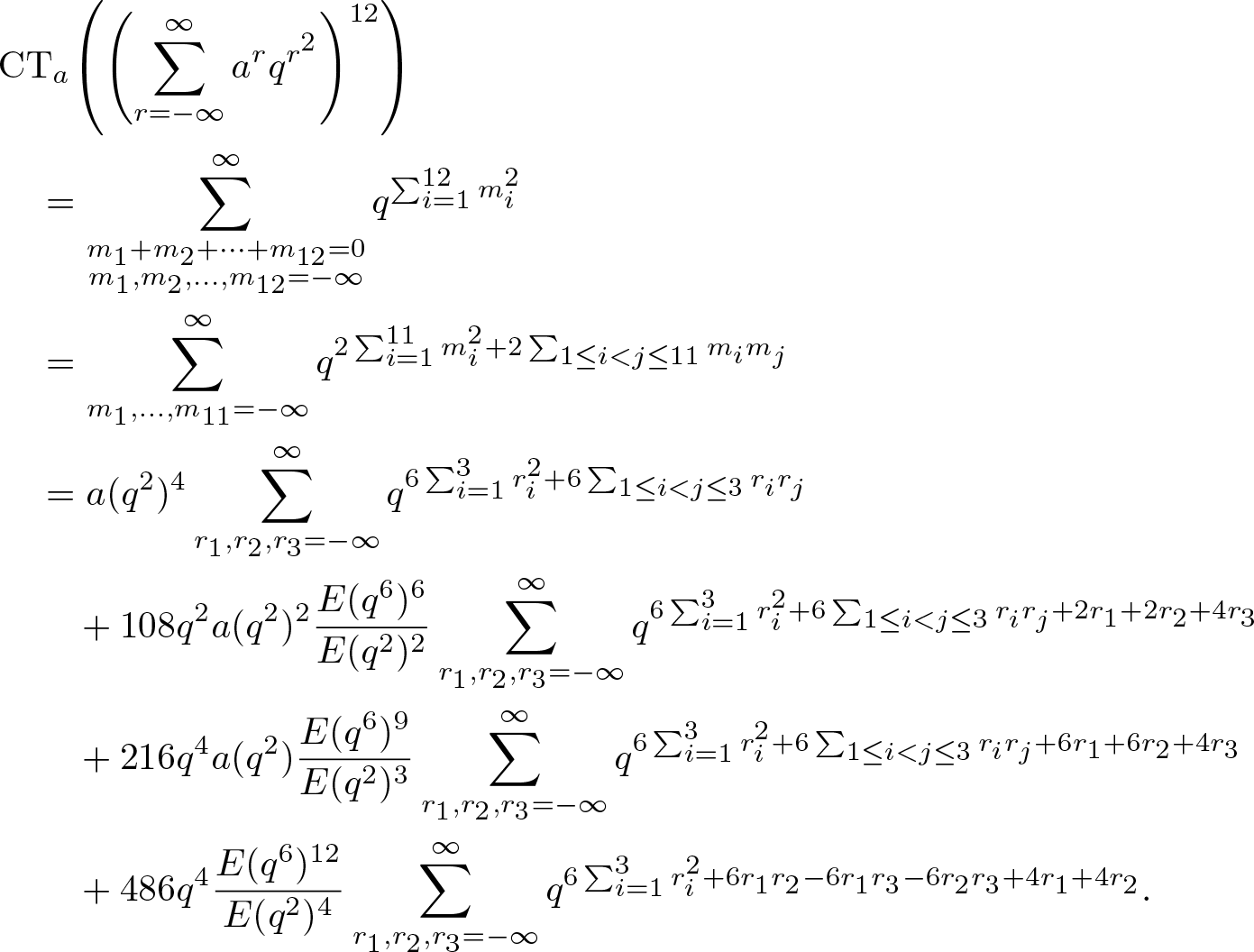 \begin{align}
&\textrm{CT}_a{\left(\left(\sum^{\infty}_{r=-\infty}
a^rq^{r^2}\right)^{12}\right)}\nonumber\\
&\quad=\sum_{\substack{m_1+m_2+\cdots+m_{12}=0\\
m_1,m_2,\ldots,m_{12}=-\infty}}^\infty q^{\sum_{i=1}^{12}m^2_i}\nonumber\\
&\quad=\sum^{\infty}_{m_1,\ldots,m_{11}=-\infty}
q^{2\sum_{i=1}^{11}m^2_i+2\sum_{1\leq i \lt j\leq11}m_im_j}\nonumber\\
&\quad=a(q^2)^4\sum^{\infty}_{r_1,r_2,r_3=-\infty}
q^{6\sum_{i=1}^3 r^2_i+6\sum_{1\leq i \lt j\leq3}r_ir_j}\nonumber\\
&\qquad+108q^2a(q^2)^2\dfrac{E(q^6)^6}{E(q^2)^2}
\sum^{\infty}_{r_1,r_2,r_3=-\infty}q^{6\sum_{i=1}^3 r^2_i
+6\sum_{1\leq i \lt j\leq3}r_ir_j+2r_1+2r_2+4r_3}\nonumber\\
&\qquad+216q^4a(q^2)\dfrac{E(q^6)^9}{E(q^2)^3}
\sum^{\infty}_{r_1,r_2,r_3=-\infty}q^{6\sum_{i=1}^3 r^2_i
+6\sum_{1\leq i \lt j\leq3}r_ir_j+6r_1+6r_2+4r_3}\nonumber\\
&\qquad+486q^4\dfrac{E(q^6)^{12}}{E(q^2)^4}
\sum^{\infty}_{r_1,r_2,r_3=-\infty}q^{6\sum_{i=1}^3 r^2_i
+6r_1r_2-6r_1r_3-6r_2r_3+4r_1+4r_2}.
\end{align}
\begin{align}
&\textrm{CT}_a{\left(\left(\sum^{\infty}_{r=-\infty}
a^rq^{r^2}\right)^{12}\right)}\nonumber\\
&\quad=\sum_{\substack{m_1+m_2+\cdots+m_{12}=0\\
m_1,m_2,\ldots,m_{12}=-\infty}}^\infty q^{\sum_{i=1}^{12}m^2_i}\nonumber\\
&\quad=\sum^{\infty}_{m_1,\ldots,m_{11}=-\infty}
q^{2\sum_{i=1}^{11}m^2_i+2\sum_{1\leq i \lt j\leq11}m_im_j}\nonumber\\
&\quad=a(q^2)^4\sum^{\infty}_{r_1,r_2,r_3=-\infty}
q^{6\sum_{i=1}^3 r^2_i+6\sum_{1\leq i \lt j\leq3}r_ir_j}\nonumber\\
&\qquad+108q^2a(q^2)^2\dfrac{E(q^6)^6}{E(q^2)^2}
\sum^{\infty}_{r_1,r_2,r_3=-\infty}q^{6\sum_{i=1}^3 r^2_i
+6\sum_{1\leq i \lt j\leq3}r_ir_j+2r_1+2r_2+4r_3}\nonumber\\
&\qquad+216q^4a(q^2)\dfrac{E(q^6)^9}{E(q^2)^3}
\sum^{\infty}_{r_1,r_2,r_3=-\infty}q^{6\sum_{i=1}^3 r^2_i
+6\sum_{1\leq i \lt j\leq3}r_ir_j+6r_1+6r_2+4r_3}\nonumber\\
&\qquad+486q^4\dfrac{E(q^6)^{12}}{E(q^2)^4}
\sum^{\infty}_{r_1,r_2,r_3=-\infty}q^{6\sum_{i=1}^3 r^2_i
+6r_1r_2-6r_1r_3-6r_2r_3+4r_1+4r_2}.
\end{align} Moreover, Andrews [Reference Andrews2, Theorem 5.2] established the following expression for ![]() $\textrm{C}\Phi_k(q)$, namely,
$\textrm{C}\Phi_k(q)$, namely,
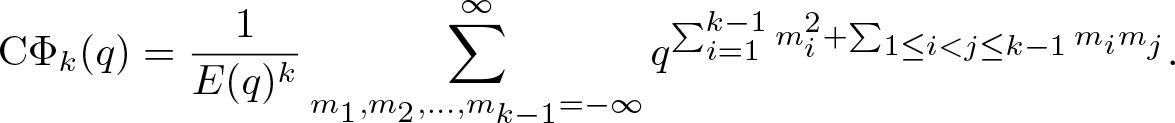 \begin{align}
\textrm{C}\Phi_k(q)=\dfrac{1}{E(q)^k}
\sum_{m_1,m_2,\ldots,m_{k-1}=-\infty}^\infty
q^{\sum_{i=1}^{k-1}m^2_i+\sum_{1\leq i \lt j\leq k-1}m_im_j}.
\end{align}
\begin{align}
\textrm{C}\Phi_k(q)=\dfrac{1}{E(q)^k}
\sum_{m_1,m_2,\ldots,m_{k-1}=-\infty}^\infty
q^{\sum_{i=1}^{k-1}m^2_i+\sum_{1\leq i \lt j\leq k-1}m_im_j}.
\end{align}The identity (1.3) follows from (3.1)–(3.4), (3.7) and (3.8).
This finishes the proof of Theorem 1.1.
Next, we are in a position to prove Theorem 1.2.
In what follows, all congruences are modulo 81 unless otherwise specified.
Proof of Theorem 1.2
According to (2.10) and (2.11), we find that
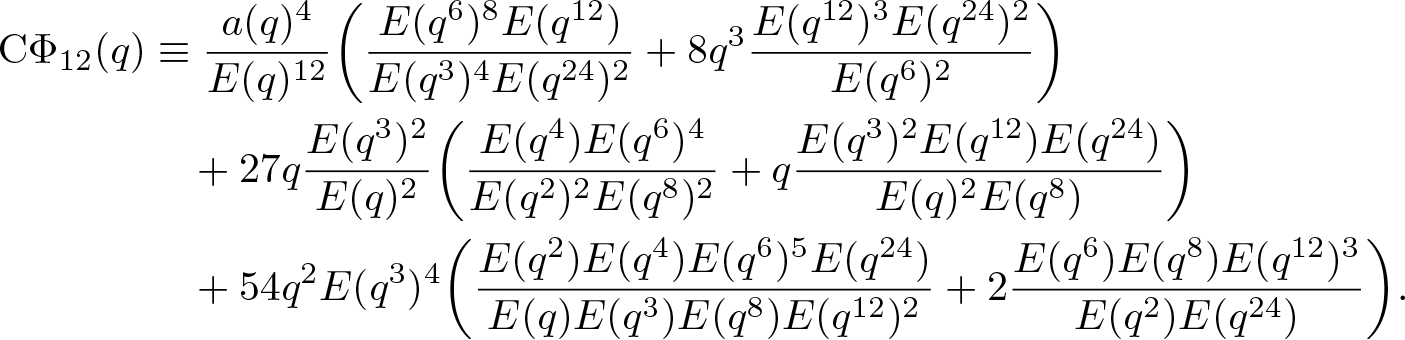 \begin{align}
\textrm{C}\Phi_{12}(q)
&\equiv\dfrac{a(q)^4}{E(q)^{12}}\bigg(\dfrac{E(q^6)^8E(q^{12})}
{E(q^3)^4E(q^{24})^2}+8q^3\dfrac{E(q^{12})^3E(q^{24})^2}{E(q^6)^2}\bigg)\nonumber\\
&\quad+27q\dfrac{E(q^3)^2}{E(q)^2}\bigg(\dfrac{E(q^4)E(q^6)^4}{E(q^2)^2E(q^8)^2}
+q\dfrac{E(q^3)^2E(q^{12})E(q^{24})}{E(q)^2E(q^8)}\bigg)\nonumber\\
&\quad+54q^2E(q^3)^4\bigg(\dfrac{E(q^2)E(q^4)E(q^6)^5E(q^{24})}
{E(q)E(q^3)E(q^8)E(q^{12})^2}+2\dfrac{E(q^6)E(q^8)E(q^{12})^3}
{E(q^2)E(q^{24})}\bigg).
\end{align}
\begin{align}
\textrm{C}\Phi_{12}(q)
&\equiv\dfrac{a(q)^4}{E(q)^{12}}\bigg(\dfrac{E(q^6)^8E(q^{12})}
{E(q^3)^4E(q^{24})^2}+8q^3\dfrac{E(q^{12})^3E(q^{24})^2}{E(q^6)^2}\bigg)\nonumber\\
&\quad+27q\dfrac{E(q^3)^2}{E(q)^2}\bigg(\dfrac{E(q^4)E(q^6)^4}{E(q^2)^2E(q^8)^2}
+q\dfrac{E(q^3)^2E(q^{12})E(q^{24})}{E(q)^2E(q^8)}\bigg)\nonumber\\
&\quad+54q^2E(q^3)^4\bigg(\dfrac{E(q^2)E(q^4)E(q^6)^5E(q^{24})}
{E(q)E(q^3)E(q^8)E(q^{12})^2}+2\dfrac{E(q^6)E(q^8)E(q^{12})^3}
{E(q^2)E(q^{24})}\bigg).
\end{align}Next, we consider the following three auxiliary functions, defined by
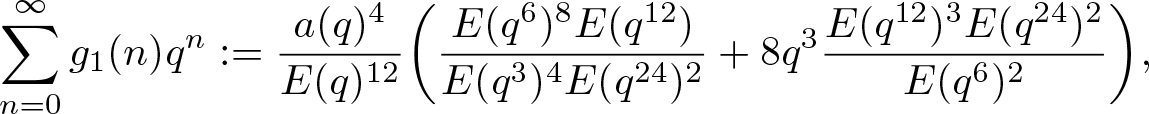 \begin{align}
\sum_{n=0}^\infty g_1(n)q^n &:=\dfrac{a(q)^4}{E(q)^{12}}
\bigg(\dfrac{E(q^6)^8E(q^{12})}{E(q^3)^4E(q^{24})^2}
+8q^3\dfrac{E(q^{12})^3E(q^{24})^2}{E(q^6)^2}\bigg),
\end{align}
\begin{align}
\sum_{n=0}^\infty g_1(n)q^n &:=\dfrac{a(q)^4}{E(q)^{12}}
\bigg(\dfrac{E(q^6)^8E(q^{12})}{E(q^3)^4E(q^{24})^2}
+8q^3\dfrac{E(q^{12})^3E(q^{24})^2}{E(q^6)^2}\bigg),
\end{align}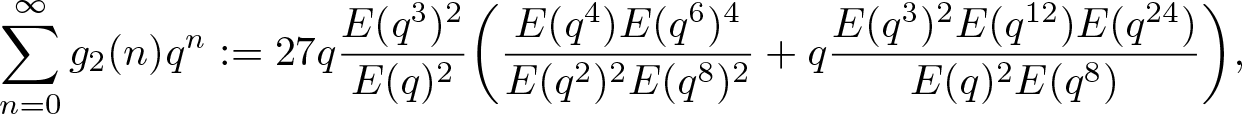 \begin{align}
\sum_{n=0}^\infty g_2(n)q^n &:=27q\dfrac{E(q^3)^2}{E(q)^2}
\bigg(\dfrac{E(q^4)E(q^6)^4}{E(q^2)^2E(q^8)^2}+q\dfrac{E(q^3)^2E
(q^{12})E(q^{24})}{E(q)^2E(q^8)}\bigg),
\end{align}
\begin{align}
\sum_{n=0}^\infty g_2(n)q^n &:=27q\dfrac{E(q^3)^2}{E(q)^2}
\bigg(\dfrac{E(q^4)E(q^6)^4}{E(q^2)^2E(q^8)^2}+q\dfrac{E(q^3)^2E
(q^{12})E(q^{24})}{E(q)^2E(q^8)}\bigg),
\end{align}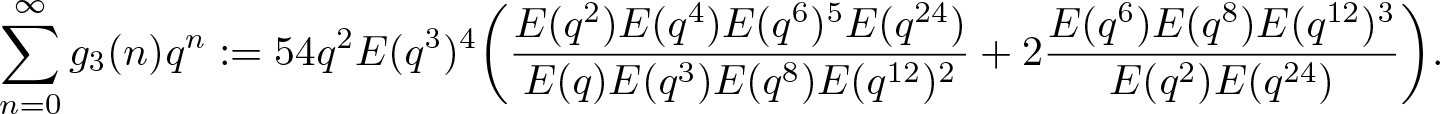 \begin{align}
\sum_{n=0}^\infty g_3(n)q^n &:=54q^2E(q^3)^4\bigg(\dfrac{E(q^2)E(q^4)
E(q^6)^5E(q^{24})}{E(q)E(q^3)E(q^8)E(q^{12})^2}+2
\dfrac{E(q^6)E(q^8)E(q^{12})^3}{E(q^2)E(q^{24})}\bigg).
\end{align}
\begin{align}
\sum_{n=0}^\infty g_3(n)q^n &:=54q^2E(q^3)^4\bigg(\dfrac{E(q^2)E(q^4)
E(q^6)^5E(q^{24})}{E(q)E(q^3)E(q^8)E(q^{12})^2}+2
\dfrac{E(q^6)E(q^8)E(q^{12})^3}{E(q^2)E(q^{24})}\bigg).
\end{align} Substituting (2.8) and (2.9) into (3.10), extracting all the terms of the form ![]() $q^{3n+2}$, after simplification, we deduce that
$q^{3n+2}$, after simplification, we deduce that
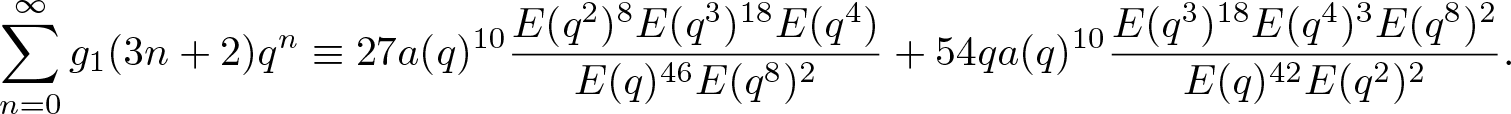 \begin{align*}
\sum_{n=0}^\infty g_1(3n+2)q^n\equiv27a(q)^{10}
\dfrac{E(q^2)^8E(q^3)^{18}E(q^4)}{E(q)^{46}E(q^8)^2}
+54qa(q)^{10}\dfrac{E(q^3)^{18}E(q^4)^3E(q^8)^2}{E(q)^{42}E(q^2)^2}.
\end{align*}
\begin{align*}
\sum_{n=0}^\infty g_1(3n+2)q^n\equiv27a(q)^{10}
\dfrac{E(q^2)^8E(q^3)^{18}E(q^4)}{E(q)^{46}E(q^8)^2}
+54qa(q)^{10}\dfrac{E(q^3)^{18}E(q^4)^3E(q^8)^2}{E(q)^{42}E(q^2)^2}.
\end{align*}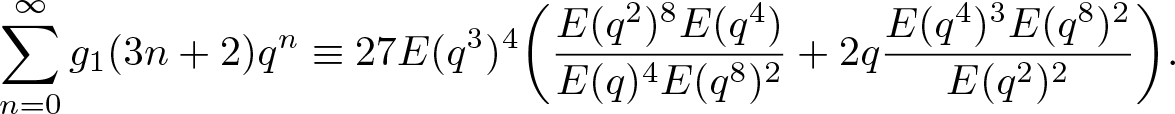 \begin{align}
\sum_{n=0}^\infty g_1(3n+2)q^n\equiv27E(q^3)^4
\bigg(\dfrac{E(q^2)^8E(q^4)}{E(q)^4E(q^8)^2}
+2q\dfrac{E(q^4)^3E(q^8)^2}{E(q^2)^2}\bigg).
\end{align}
\begin{align}
\sum_{n=0}^\infty g_1(3n+2)q^n\equiv27E(q^3)^4
\bigg(\dfrac{E(q^2)^8E(q^4)}{E(q)^4E(q^8)^2}
+2q\dfrac{E(q^4)^3E(q^8)^2}{E(q^2)^2}\bigg).
\end{align}The congruence (1.5) follows from (3.9) and (3.13) immediately.
Moreover, it follows from (3.13) that
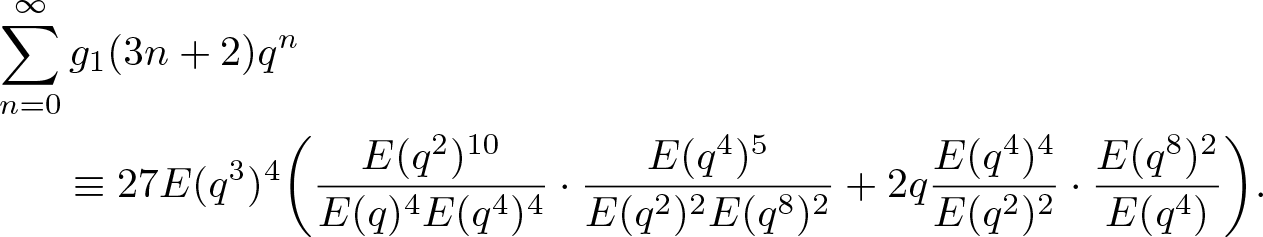 \begin{align}
\sum_{n=0}^\infty &\,g_1(3n+2)q^n\nonumber\\
&\equiv27E(q^3)^4\bigg(\dfrac{E(q^2)^{10}}{E(q)^4E(q^4)^4}
\cdot\dfrac{E(q^4)^5}{E(q^2)^2E(q^8)^2}
+2q\dfrac{E(q^4)^4}{E(q^2)^2}\cdot
\dfrac{E(q^8)^2}{E(q^4)}\bigg).
\end{align}
\begin{align}
\sum_{n=0}^\infty &\,g_1(3n+2)q^n\nonumber\\
&\equiv27E(q^3)^4\bigg(\dfrac{E(q^2)^{10}}{E(q)^4E(q^4)^4}
\cdot\dfrac{E(q^4)^5}{E(q^2)^2E(q^8)^2}
+2q\dfrac{E(q^4)^4}{E(q^2)^2}\cdot
\dfrac{E(q^8)^2}{E(q^4)}\bigg).
\end{align}Substituting (2.3) and (2.4) into (3.14), after some tedious but straightforward calculations, we deduce that
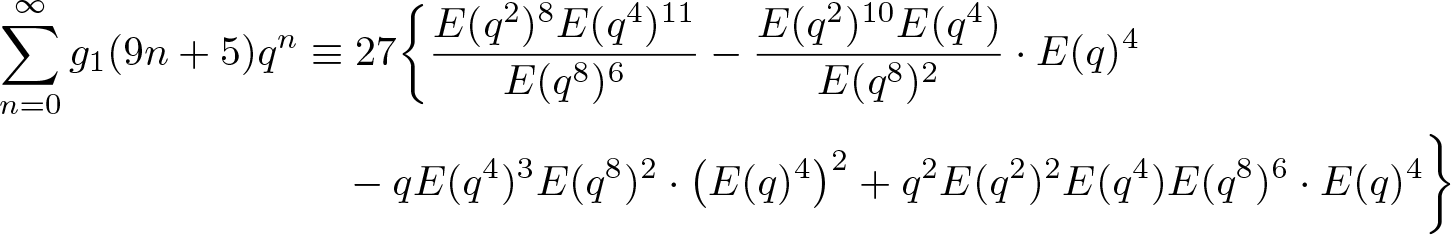 \begin{align}
\sum_{n=0}^\infty g_1(9n+5)q^n &\equiv27\bigg\{\dfrac{E(q^2)^8E(q^4)^{11}}
{E(q^8)^6}-\dfrac{E(q^2)^{10}E(q^4)}{E(q^8)^2}\cdot E(q)^4\notag\\
&\quad-qE(q^4)^3E(q^8)^2\cdot\big(E(q)^4\big)^2
+q^2E(q^2)^2E(q^4)E(q^8)^6\cdot E(q)^4\bigg\}
\end{align}
\begin{align}
\sum_{n=0}^\infty g_1(9n+5)q^n &\equiv27\bigg\{\dfrac{E(q^2)^8E(q^4)^{11}}
{E(q^8)^6}-\dfrac{E(q^2)^{10}E(q^4)}{E(q^8)^2}\cdot E(q)^4\notag\\
&\quad-qE(q^4)^3E(q^8)^2\cdot\big(E(q)^4\big)^2
+q^2E(q^2)^2E(q^4)E(q^8)^6\cdot E(q)^4\bigg\}
\end{align}and
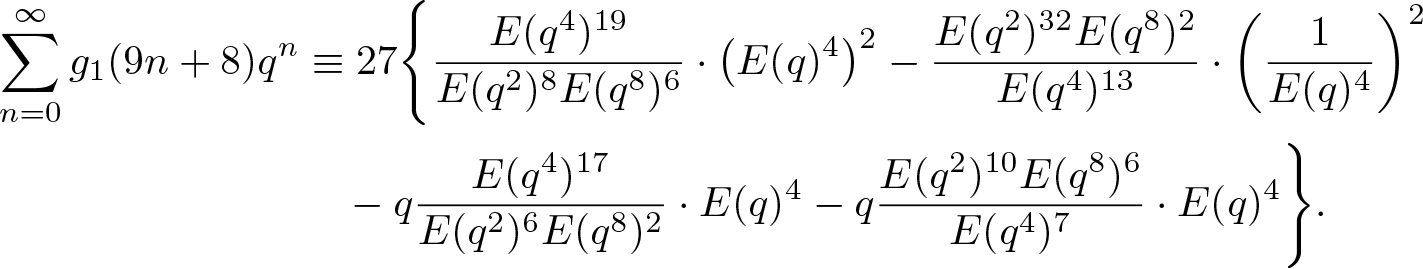 \begin{align}
\sum_{n=0}^\infty g_1(9n+8)q^n &\equiv27\Bigg\{\dfrac{E(q^4)^{19}}
{E(q^2)^8E(q^8)^6}\cdot\big(E(q)^4\big)^2
-\dfrac{E(q^2)^{32}E(q^8)^2}{E(q^4)^{13}}\cdot
\bigg(\dfrac{1}{E(q)^4}\bigg)^2\nonumber\\
&\quad-q\dfrac{E(q^4)^{17}}{E(q^2)^6E(q^8)^2}\cdot E(q)^4
-q\dfrac{E(q^2)^{10}E(q^8)^6}{E(q^4)^7}\cdot E(q)^4\Bigg\}.
\end{align}
\begin{align}
\sum_{n=0}^\infty g_1(9n+8)q^n &\equiv27\Bigg\{\dfrac{E(q^4)^{19}}
{E(q^2)^8E(q^8)^6}\cdot\big(E(q)^4\big)^2
-\dfrac{E(q^2)^{32}E(q^8)^2}{E(q^4)^{13}}\cdot
\bigg(\dfrac{1}{E(q)^4}\bigg)^2\nonumber\\
&\quad-q\dfrac{E(q^4)^{17}}{E(q^2)^6E(q^8)^2}\cdot E(q)^4
-q\dfrac{E(q^2)^{10}E(q^8)^6}{E(q^4)^7}\cdot E(q)^4\Bigg\}.
\end{align}Substituting (2.1) and (2.2) into (31.5) and (3.16), upon simplification, we further obtain that
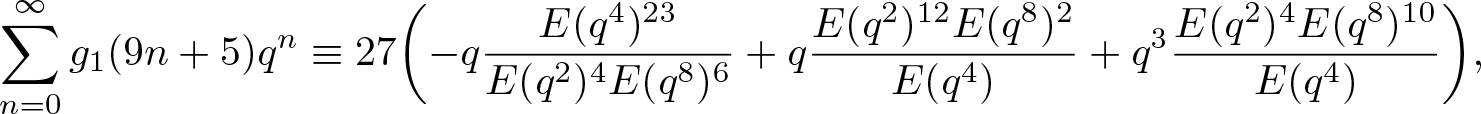 \begin{align}
\sum_{n=0}^\infty g_1(9n+5)q^n &\equiv27\bigg({-}q\dfrac{E(q^4)^{23}}
{E(q^2)^4E(q^8)^6}+q\dfrac{E(q^2)^{12}E(q^8)^2}{E(q^4)}
+q^3\dfrac{E(q^2)^4E(q^8)^{10}}{E(q^4)}\bigg),
\end{align}
\begin{align}
\sum_{n=0}^\infty g_1(9n+5)q^n &\equiv27\bigg({-}q\dfrac{E(q^4)^{23}}
{E(q^2)^4E(q^8)^6}+q\dfrac{E(q^2)^{12}E(q^8)^2}{E(q^4)}
+q^3\dfrac{E(q^2)^4E(q^8)^{10}}{E(q^4)}\bigg),
\end{align}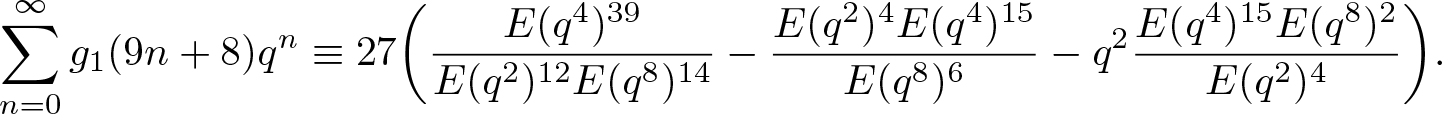 \begin{align}
\sum_{n=0}^\infty g_1(9n+8)q^n &\equiv27\bigg(\dfrac{E(q^4)^{39}}
{E(q^2)^{12}E(q^8)^{14}}-\dfrac{E(q^2)^4E(q^4)^{15}}{E(q^8)^6}
-q^2\dfrac{E(q^4)^{15}E(q^8)^2}{E(q^2)^4}\bigg).
\end{align}
\begin{align}
\sum_{n=0}^\infty g_1(9n+8)q^n &\equiv27\bigg(\dfrac{E(q^4)^{39}}
{E(q^2)^{12}E(q^8)^{14}}-\dfrac{E(q^2)^4E(q^4)^{15}}{E(q^8)^6}
-q^2\dfrac{E(q^4)^{15}E(q^8)^2}{E(q^2)^4}\bigg).
\end{align}Now, we recall Horschhorn’s version of parameterized identities (see [Reference Hirschhorn17, Chapter 35, Equations (35.1.1)–(35.1.6)]), whose idea comes from [Reference Alaca, Alaca and Williams1].
where
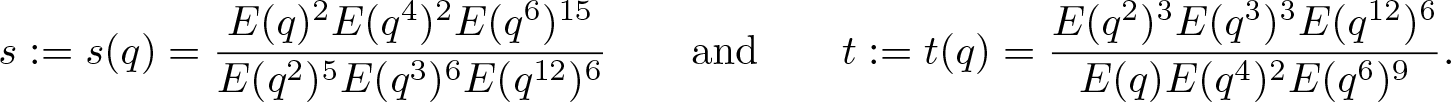 \begin{align*}
s:=s(q)=\dfrac{E(q)^2E(q^4)^2E(q^6)^{15}}{E(q^2)^5E(q^3)^6E(q^{12})^6}
\qquad\textrm{and}\qquad
t:=t(q)=\dfrac{E(q^2)^3E(q^3)^3E(q^{12})^6}{E(q)E(q^4)^2E(q^6)^9}.
\end{align*}
\begin{align*}
s:=s(q)=\dfrac{E(q)^2E(q^4)^2E(q^6)^{15}}{E(q^2)^5E(q^3)^6E(q^{12})^6}
\qquad\textrm{and}\qquad
t:=t(q)=\dfrac{E(q^2)^3E(q^3)^3E(q^{12})^6}{E(q)E(q^4)^2E(q^6)^9}.
\end{align*}It follows immediately from the parameterized identities (3.19)–(3.24) that
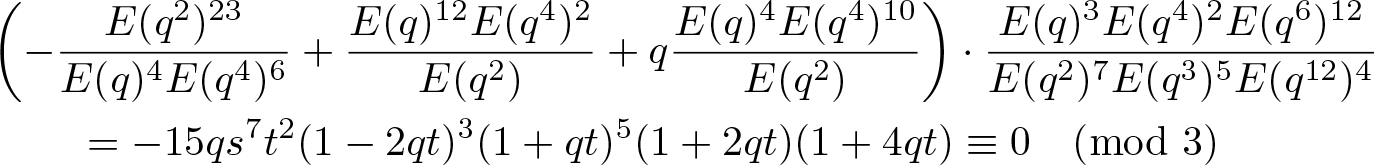 \begin{align*}
&{\left({-}\dfrac{E(q^2)^{23}}{E(q)^4E(q^4)^6}+\dfrac{E(q)^{12}E(q^4)^2}{E(q^2)}
+q\dfrac{E(q)^4E(q^4)^{10}}{E(q^2)}\right)}
\cdot\dfrac{E(q)^3E(q^4)^2E(q^6)^{12}}{E(q^2)^7E(q^3)^5E(q^{12})^4}\\
&\qquad=-15qs^7t^2(1-2qt)^3(1+qt)^5(1+2qt)(1+4qt)\equiv0\pmod{3}
\end{align*}
\begin{align*}
&{\left({-}\dfrac{E(q^2)^{23}}{E(q)^4E(q^4)^6}+\dfrac{E(q)^{12}E(q^4)^2}{E(q^2)}
+q\dfrac{E(q)^4E(q^4)^{10}}{E(q^2)}\right)}
\cdot\dfrac{E(q)^3E(q^4)^2E(q^6)^{12}}{E(q^2)^7E(q^3)^5E(q^{12})^4}\\
&\qquad=-15qs^7t^2(1-2qt)^3(1+qt)^5(1+2qt)(1+4qt)\equiv0\pmod{3}
\end{align*}and
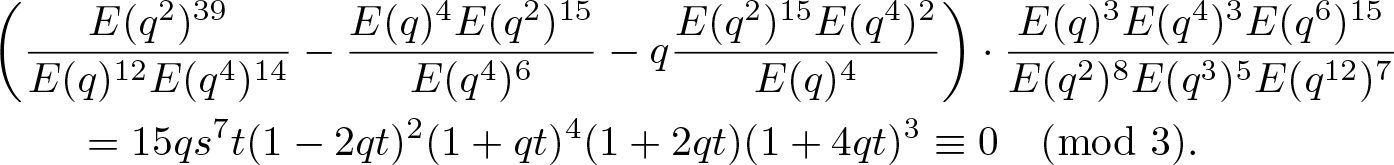 \begin{align*}
&{\left(\dfrac{E(q^2)^{39}}{E(q)^{12}E(q^4)^{14}}
-\dfrac{E(q)^4E(q^2)^{15}}{E(q^4)^6}-q\dfrac{E(q^2)^{15}E(q^4)^2}{E(q)^4}\right)}\cdot
\dfrac{E(q)^3E(q^4)^3E(q^6)^{15}}{E(q^2)^8E(q^3)^5E(q^{12})^7}\\
&\qquad=15qs^7t(1-2qt)^2(1+qt)^4(1+2qt)(1+4qt)^3\equiv0\pmod{3}.
\end{align*}
\begin{align*}
&{\left(\dfrac{E(q^2)^{39}}{E(q)^{12}E(q^4)^{14}}
-\dfrac{E(q)^4E(q^2)^{15}}{E(q^4)^6}-q\dfrac{E(q^2)^{15}E(q^4)^2}{E(q)^4}\right)}\cdot
\dfrac{E(q)^3E(q^4)^3E(q^6)^{15}}{E(q^2)^8E(q^3)^5E(q^{12})^7}\\
&\qquad=15qs^7t(1-2qt)^2(1+qt)^4(1+2qt)(1+4qt)^3\equiv0\pmod{3}.
\end{align*}Since
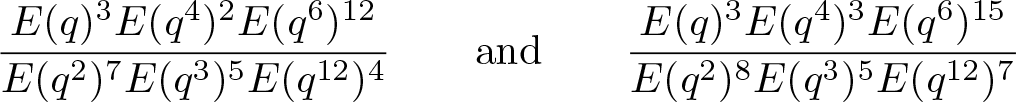 \begin{align*}
\dfrac{E(q)^3E(q^4)^2E(q^6)^{12}}{E(q^2)^7E(q^3)^5E(q^{12})^4}
\qquad\textrm{and}\qquad\dfrac{E(q)^3E(q^4)^3E(q^6)^{15}}{E(q^2)^8E(q^3)^5E(q^{12})^7}
\end{align*}
\begin{align*}
\dfrac{E(q)^3E(q^4)^2E(q^6)^{12}}{E(q^2)^7E(q^3)^5E(q^{12})^4}
\qquad\textrm{and}\qquad\dfrac{E(q)^3E(q^4)^3E(q^6)^{15}}{E(q^2)^8E(q^3)^5E(q^{12})^7}
\end{align*} are invertible in the ring ![]() $\mathbb{Z}/3\mathbb{Z}[[q]]$, we deduce that
$\mathbb{Z}/3\mathbb{Z}[[q]]$, we deduce that
 \begin{align}
-\dfrac{E(q^2)^{23}}{E(q)^4E(q^4)^6}+\dfrac{E(q)^{12}E(q^4)^2}{E(q^2)}
+q\dfrac{E(q)^4E(q^4)^{10}}{E(q^2)}
&\equiv0\pmod{3},
\end{align}
\begin{align}
-\dfrac{E(q^2)^{23}}{E(q)^4E(q^4)^6}+\dfrac{E(q)^{12}E(q^4)^2}{E(q^2)}
+q\dfrac{E(q)^4E(q^4)^{10}}{E(q^2)}
&\equiv0\pmod{3},
\end{align}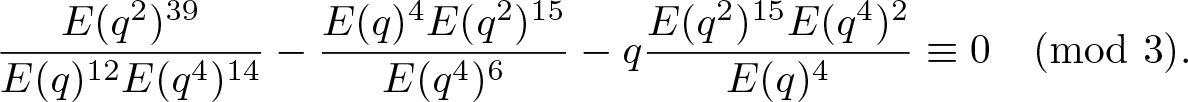 \begin{align}
\dfrac{E(q^2)^{39}}{E(q)^{12}E(q^4)^{14}}-\dfrac{E(q)^4E(q^2)^{15}}{E(q^4)^6}
-q\dfrac{E(q^2)^{15}E(q^4)^2}{E(q)^4}
&\equiv0\pmod{3}.
\end{align}
\begin{align}
\dfrac{E(q^2)^{39}}{E(q)^{12}E(q^4)^{14}}-\dfrac{E(q)^4E(q^2)^{15}}{E(q^4)^6}
-q\dfrac{E(q^2)^{15}E(q^4)^2}{E(q)^4}
&\equiv0\pmod{3}.
\end{align} The congruences (3.17) and (3.18), together with (3.25) and (3.26), imply that for any ![]() $n\geq0$,
$n\geq0$,
Similarly, from (3.11), we find that
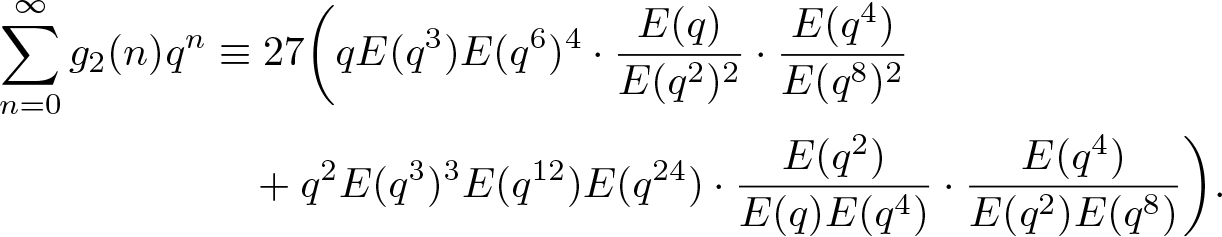 \begin{align*}
\sum_{n=0}^\infty g_2(n)q^n &\equiv27\bigg(qE(q^3)E(q^6)^4\cdot
\dfrac{E(q)}{E(q^2)^2}\cdot\dfrac{E(q^4)}{E(q^8)^2}\\
&\quad+q^2E(q^3)^3E(q^{12})E(q^{24})\cdot\dfrac{E(q^2)}{E(q)E(q^4)}
\cdot\dfrac{E(q^4)}{E(q^2)E(q^8)}\bigg).
\end{align*}
\begin{align*}
\sum_{n=0}^\infty g_2(n)q^n &\equiv27\bigg(qE(q^3)E(q^6)^4\cdot
\dfrac{E(q)}{E(q^2)^2}\cdot\dfrac{E(q^4)}{E(q^8)^2}\\
&\quad+q^2E(q^3)^3E(q^{12})E(q^{24})\cdot\dfrac{E(q^2)}{E(q)E(q^4)}
\cdot\dfrac{E(q^4)}{E(q^2)E(q^8)}\bigg).
\end{align*}With the help of (2.6) and (2.7), we further obtain that
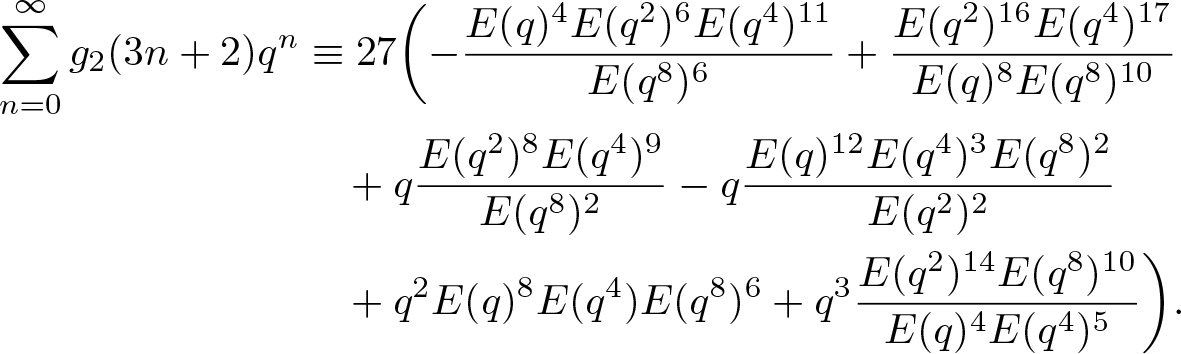 \begin{align}
\sum_{n=0}^\infty g_2(3n+2)q^n
&\equiv27\bigg({-}\dfrac{E(q)^4E(q^2)^6E(q^4)^{11}}{E(q^8)^6}
+\dfrac{E(q^2)^{16}E(q^4)^{17}}{E(q)^8E(q^8)^{10}}\nonumber\\
&\quad+q\dfrac{E(q^2)^8E(q^4)^9}{E(q^8)^2}
-q\dfrac{E(q)^{12}E(q^4)^3E(q^8)^2}{E(q^2)^2}\nonumber\\
&\quad+q^2E(q)^8E(q^4)E(q^8)^6
+q^3\dfrac{E(q^2)^{14}E(q^8)^{10}}{E(q)^4E(q^4)^5}\bigg).
\end{align}
\begin{align}
\sum_{n=0}^\infty g_2(3n+2)q^n
&\equiv27\bigg({-}\dfrac{E(q)^4E(q^2)^6E(q^4)^{11}}{E(q^8)^6}
+\dfrac{E(q^2)^{16}E(q^4)^{17}}{E(q)^8E(q^8)^{10}}\nonumber\\
&\quad+q\dfrac{E(q^2)^8E(q^4)^9}{E(q^8)^2}
-q\dfrac{E(q)^{12}E(q^4)^3E(q^8)^2}{E(q^2)^2}\nonumber\\
&\quad+q^2E(q)^8E(q^4)E(q^8)^6
+q^3\dfrac{E(q^2)^{14}E(q^8)^{10}}{E(q)^4E(q^4)^5}\bigg).
\end{align}Plugging (2.1) and (2.2) into (3.28), after simplification, we obtain that
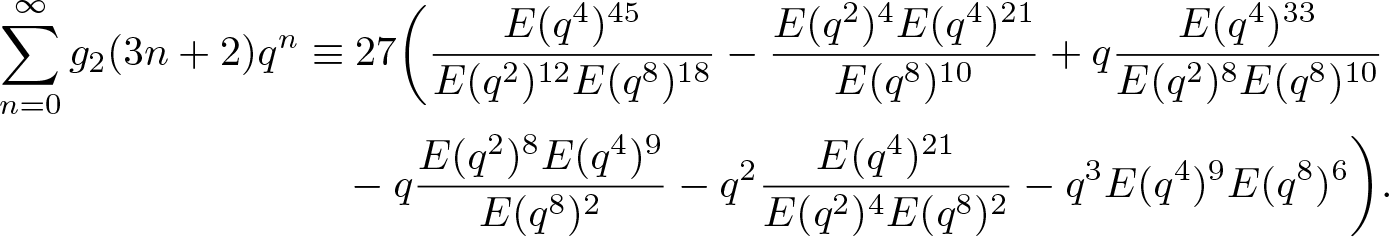 \begin{align}
\sum_{n=0}^\infty g_2(3n+2)q^n &\equiv
27\bigg(\dfrac{E(q^4)^{45}}{E(q^2)^{12}E(q^8)^{18}}
-\dfrac{E(q^2)^4E(q^4)^{21}}{E(q^8)^{10}}
+q\dfrac{E(q^4)^{33}}{E(q^2)^8E(q^8)^{10}}\nonumber\\
&\quad-q\dfrac{E(q^2)^8E(q^4)^9}{E(q^8)^2}
-q^2\dfrac{E(q^4)^{21}}{E(q^2)^4E(q^8)^2}-q^3E(q^4)^9E(q^8)^6\bigg).
\end{align}
\begin{align}
\sum_{n=0}^\infty g_2(3n+2)q^n &\equiv
27\bigg(\dfrac{E(q^4)^{45}}{E(q^2)^{12}E(q^8)^{18}}
-\dfrac{E(q^2)^4E(q^4)^{21}}{E(q^8)^{10}}
+q\dfrac{E(q^4)^{33}}{E(q^2)^8E(q^8)^{10}}\nonumber\\
&\quad-q\dfrac{E(q^2)^8E(q^4)^9}{E(q^8)^2}
-q^2\dfrac{E(q^4)^{21}}{E(q^2)^4E(q^8)^2}-q^3E(q^4)^9E(q^8)^6\bigg).
\end{align}According to the parameterized identities (3.19)–(3.24), we find that
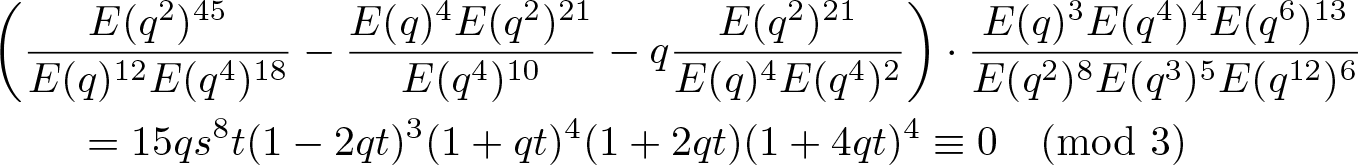 \begin{align*}
&{\left(\dfrac{E(q^2)^{45}}{E(q)^{12}E(q^4)^{18}}
-\dfrac{E(q)^4E(q^2)^{21}}{E(q^4)^{10}}
-q\dfrac{E(q^2)^{21}}{E(q)^4E(q^4)^2}\right)}\cdot
\dfrac{E(q)^3E(q^4)^4E(q^6)^{13}}{E(q^2)^8E(q^3)^5E(q^{12})^6}\nonumber\\
&\qquad=15qs^8t(1-2qt)^3(1+qt)^4(1+2qt)(1+4qt)^4\equiv0\pmod{3}
\end{align*}
\begin{align*}
&{\left(\dfrac{E(q^2)^{45}}{E(q)^{12}E(q^4)^{18}}
-\dfrac{E(q)^4E(q^2)^{21}}{E(q^4)^{10}}
-q\dfrac{E(q^2)^{21}}{E(q)^4E(q^4)^2}\right)}\cdot
\dfrac{E(q)^3E(q^4)^4E(q^6)^{13}}{E(q^2)^8E(q^3)^5E(q^{12})^6}\nonumber\\
&\qquad=15qs^8t(1-2qt)^3(1+qt)^4(1+2qt)(1+4qt)^4\equiv0\pmod{3}
\end{align*}and
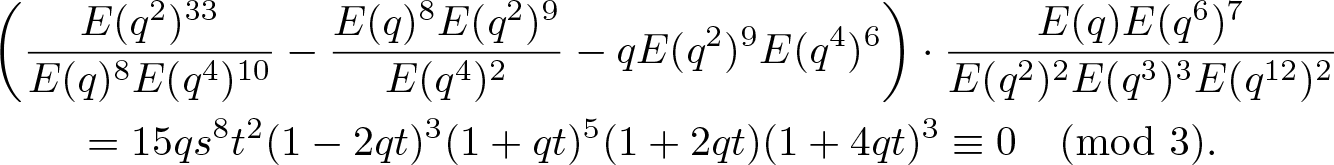 \begin{align*}
&{\left(\dfrac{E(q^2)^{33}}{E(q)^8E(q^4)^{10}}-\dfrac{E(q)^8E(q^2)^9}{E(q^4)^2}
-qE(q^2)^9E(q^4)^6\right)}\cdot
\dfrac{E(q)E(q^6)^7}{E(q^2)^2E(q^3)^3E(q^{12})^2}\\
&\qquad=15qs^8t^2(1-2qt)^3(1+qt)^5(1+2qt)(1+4qt)^3\equiv0\pmod{3}.
\end{align*}
\begin{align*}
&{\left(\dfrac{E(q^2)^{33}}{E(q)^8E(q^4)^{10}}-\dfrac{E(q)^8E(q^2)^9}{E(q^4)^2}
-qE(q^2)^9E(q^4)^6\right)}\cdot
\dfrac{E(q)E(q^6)^7}{E(q^2)^2E(q^3)^3E(q^{12})^2}\\
&\qquad=15qs^8t^2(1-2qt)^3(1+qt)^5(1+2qt)(1+4qt)^3\equiv0\pmod{3}.
\end{align*}Since
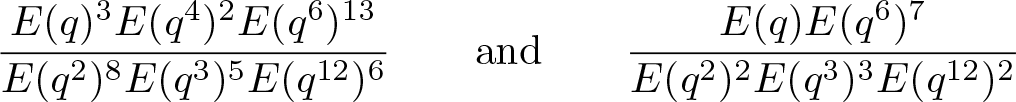 \begin{align*}
\dfrac{E(q)^3E(q^4)^2E(q^6)^{13}}{E(q^2)^8E(q^3)^5E(q^{12})^6}
\qquad\textrm{and}\qquad\dfrac{E(q)E(q^6)^7}{E(q^2)^2E(q^3)^3E(q^{12})^2}
\end{align*}
\begin{align*}
\dfrac{E(q)^3E(q^4)^2E(q^6)^{13}}{E(q^2)^8E(q^3)^5E(q^{12})^6}
\qquad\textrm{and}\qquad\dfrac{E(q)E(q^6)^7}{E(q^2)^2E(q^3)^3E(q^{12})^2}
\end{align*} are invertible in the ring ![]() $\mathbb{Z}/3\mathbb{Z}[[q]]$, we obtain that
$\mathbb{Z}/3\mathbb{Z}[[q]]$, we obtain that
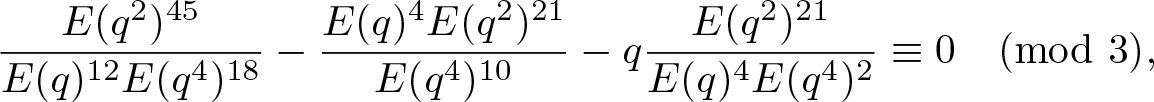 \begin{align}
\dfrac{E(q^2)^{45}}{E(q)^{12}E(q^4)^{18}}
-\dfrac{E(q)^4E(q^2)^{21}}{E(q^4)^{10}}
-q\dfrac{E(q^2)^{21}}{E(q)^4E(q^4)^2} &\equiv0\pmod{3},
\end{align}
\begin{align}
\dfrac{E(q^2)^{45}}{E(q)^{12}E(q^4)^{18}}
-\dfrac{E(q)^4E(q^2)^{21}}{E(q^4)^{10}}
-q\dfrac{E(q^2)^{21}}{E(q)^4E(q^4)^2} &\equiv0\pmod{3},
\end{align}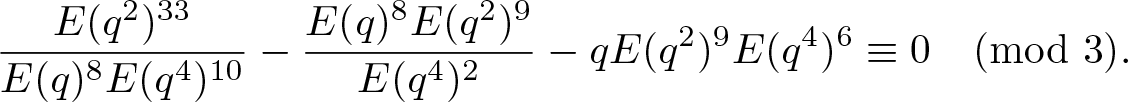 \begin{align}
\dfrac{E(q^2)^{33}}{E(q)^8E(q^4)^{10}}
-\dfrac{E(q)^8E(q^2)^9}{E(q^4)^2}-qE(q^2)^9E(q^4)^6
&\equiv0\pmod{3}.
\end{align}
\begin{align}
\dfrac{E(q^2)^{33}}{E(q)^8E(q^4)^{10}}
-\dfrac{E(q)^8E(q^2)^9}{E(q^4)^2}-qE(q^2)^9E(q^4)^6
&\equiv0\pmod{3}.
\end{align} According to (3.29)–(3.31), we find that for any ![]() $n\geq0$,
$n\geq0$,
Finally, from (3.12), we find that
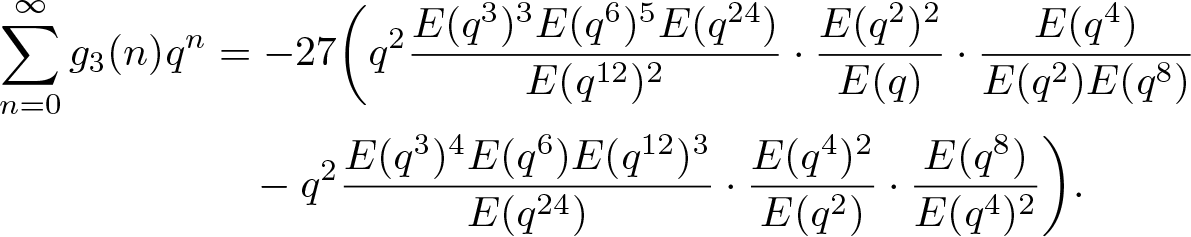 \begin{align*}
\sum_{n=0}^\infty g_3(n)q^n &=-27
\bigg(q^2\dfrac{E(q^3)^3E(q^6)^5E(q^{24})}{E(q^{12})^2}
\cdot\dfrac{E(q^2)^2}{E(q)}\cdot\dfrac{E(q^4)}{E(q^2)E(q^8)}\nonumber\\
&\quad-q^2\dfrac{E(q^3)^4E(q^6)E(q^{12})^3}{E(q^{24})}
\cdot\dfrac{E(q^4)^2}{E(q^2)}\cdot\dfrac{E(q^8)}{E(q^4)^2}\bigg).
\end{align*}
\begin{align*}
\sum_{n=0}^\infty g_3(n)q^n &=-27
\bigg(q^2\dfrac{E(q^3)^3E(q^6)^5E(q^{24})}{E(q^{12})^2}
\cdot\dfrac{E(q^2)^2}{E(q)}\cdot\dfrac{E(q^4)}{E(q^2)E(q^8)}\nonumber\\
&\quad-q^2\dfrac{E(q^3)^4E(q^6)E(q^{12})^3}{E(q^{24})}
\cdot\dfrac{E(q^4)^2}{E(q^2)}\cdot\dfrac{E(q^8)}{E(q^4)^2}\bigg).
\end{align*}Thanks to (2.4), (2.5), (2.7) and (2.11), we further arrive at
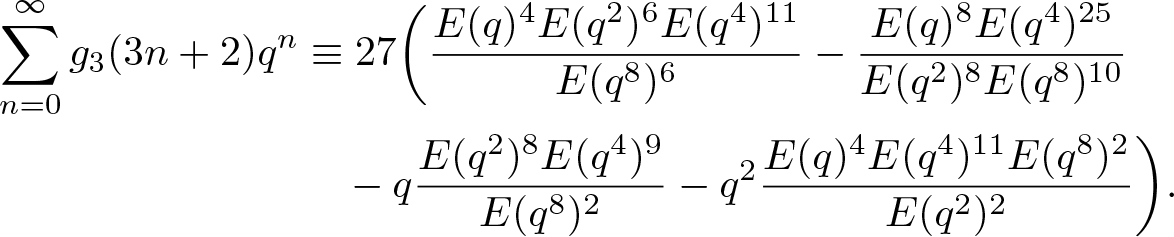 \begin{align}
\sum_{n=0}^\infty g_3(3n+2)q^n &\equiv27
\bigg(\dfrac{E(q)^4E(q^2)^6E(q^4)^{11}}{E(q^8)^6}
-\dfrac{E(q)^8E(q^4)^{25}}{E(q^2)^8E(q^8)^{10}}\nonumber\\
&\quad-q\dfrac{E(q^2)^8E(q^4)^9}{E(q^8)^2}
-q^2\dfrac{E(q)^4E(q^4)^{11}E(q^8)^2}{E(q^2)^2}\bigg).
\end{align}
\begin{align}
\sum_{n=0}^\infty g_3(3n+2)q^n &\equiv27
\bigg(\dfrac{E(q)^4E(q^2)^6E(q^4)^{11}}{E(q^8)^6}
-\dfrac{E(q)^8E(q^4)^{25}}{E(q^2)^8E(q^8)^{10}}\nonumber\\
&\quad-q\dfrac{E(q^2)^8E(q^4)^9}{E(q^8)^2}
-q^2\dfrac{E(q)^4E(q^4)^{11}E(q^8)^2}{E(q^2)^2}\bigg).
\end{align}Substituting (2.1) into (3.33), upon simplification, we obtain that
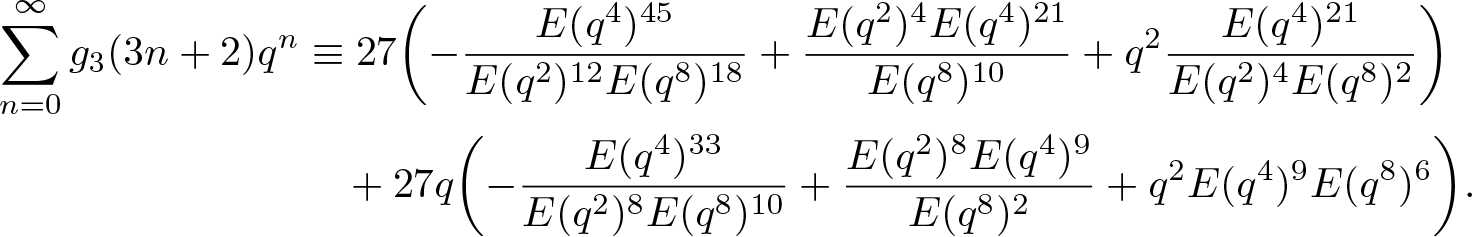 \begin{align*}
\sum_{n=0}^\infty g_3(3n+2)q^n
&\equiv27\bigg({-}\dfrac{E(q^4)^{45}}{E(q^2)^{12}E(q^8)^{18}}
+\dfrac{E(q^2)^4E(q^4)^{21}}{E(q^8)^{10}}
+q^2\dfrac{E(q^4)^{21}}{E(q^2)^4E(q^8)^2}\bigg)\\
&\quad+27q\bigg({-}\dfrac{E(q^4)^{33}}{E(q^2)^8E(q^8)^{10}}
+\dfrac{E(q^2)^8E(q^4)^9}{E(q^8)^2}+q^2E(q^4)^9E(q^8)^6\bigg).
\end{align*}
\begin{align*}
\sum_{n=0}^\infty g_3(3n+2)q^n
&\equiv27\bigg({-}\dfrac{E(q^4)^{45}}{E(q^2)^{12}E(q^8)^{18}}
+\dfrac{E(q^2)^4E(q^4)^{21}}{E(q^8)^{10}}
+q^2\dfrac{E(q^4)^{21}}{E(q^2)^4E(q^8)^2}\bigg)\\
&\quad+27q\bigg({-}\dfrac{E(q^4)^{33}}{E(q^2)^8E(q^8)^{10}}
+\dfrac{E(q^2)^8E(q^4)^9}{E(q^8)^2}+q^2E(q^4)^9E(q^8)^6\bigg).
\end{align*} According to (3.30) and (3.31), we conclude that for any ![]() $n\geq0$,
$n\geq0$,
The congruences (1.6) and (1.7) follow from (3.9)–(3.12), (3.27), (3.32) and (3.34).
We therefore complete the proof of Theorem 1.2.
Acknowledgements
The authors would like to acknowledge two anonymous referees for their careful reading and many helpful suggestions, which improved the quality of this paper to a great extent.
Funding Statement
Su-Ping Cui was partially supported by the National Natural Science Foundation of China (No. 12001309) and the Foreign Youth Exchange Program of China Association of Science and Technology. Nancy S. S. Gu was partially supported by the National Natural Science Foundation of China (No. 12171255). Dazhao Tang is the corresponding author. Dazhao Tang was partially supported by the National Natural Science Foundation of China (No. 12201093), the Natural Science Foundation Project of Chongqing CSTB (No. CSTB2022NSCQ–MSX0387), the Science and Technology Research Program of Chongqing Municipal Education Commission (No. KJQN202200509) and the Doctoral start-up research grant (No. 21XLB038) of Chongqing Normal University.