Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T06:05:57.035Z Has data issue: false hasContentIssue false
  • English
  • Français

Solutions of first level of meromorphic differential equations

Published online by Cambridge University Press:  20 January 2009

W. Balser
W. Balser
Affiliation:
Abt. Mathematik V, Universität Ulm, D-7900 Ulm, West Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let a meromorphic differential equation

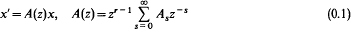
be given, where r is an integer, and the series converges for |z| sufficiently large. Then it is well known that (0.1) is formally satisfied by an expression

where F( z) is a formal power series in z–1 times an integer power of z, and F( z) has an inverse of the same kind, L is a constant matrix, and

is a diagonal matrix of polynomials qj( z) in a root of z, 1≦ j≦ n. If, for example, all the polynomials in Q( z) are equal, then F( z) can be seen to be a convergent series (see Section 1), whereas if not, then generally the coefficients in F( z) grow so rapidly that F( z) diverges for every (finite) z.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 25 , Issue 2 , June 1982 , pp. 183 - 207
Copyright
Copyright © Edinburgh Mathematical Society 1982

References

REFERENCES

1.Balser, W., Einige Beiträge zur Invariantentheorie meromorpher Differentialgleichungen (Habilitationsschrift, Ulm, 1978).Google Scholar
2.Balser, W., Zum Einzigkeitssatz in der Invariantentheorie meromorpher Differentialgleichungen, J. reine u. angew. Math. 318 (1980), 51–82.Google Scholar
3.Balser, W., Jurkat, W. B. and Lutz, D. A., A general theory of invariants for meromorphic differential equations. I, formal invariants, Funk. Ekvac. 22 (1979), 197–221.Google Scholar
4.Balser, W., Jurkat, W. B. and Lutz, D. A., A general theory of invariants for meromorphic differential equations. II, proper invariants, Funk. Ekvac. 22 (1979), 257–283.Google Scholar
5.Balser, W., Jurkat, W. B. and Lutz, D. A., The invariants of reducible meromorphic differential equations, Proc. Edinburgh Math. Soc. 23 (1980), 163–187.CrossRefGoogle Scholar
6.Coddington, E. A. and Levinson, N., Theory of Ordinary Differential Equations (New York-Toronto-London, 1955).Google Scholar
7.Jurkat, W. B., Meromorphe Differentialgleichungen (Lecture Notes in Mathematics 637, Berlin-Heidelberg-New York, 1978).CrossRefGoogle Scholar
8.Sibuya, Y., Linear differential equations in the complex domain, Problems of Analytic Continuation (on Japanese) (Kinokuniya, 1976).Google Scholar
9.Sibuya, Y., Stokes' Phenomena, Bull. Amer. Math. Soc. 83 (1977), 1075–1077.CrossRefGoogle Scholar
10.Wasow, W., Asymptotic Expansions for Ordinary Differential Equations (New York, 1956).Google Scholar