Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Felten, Simon
Filip, Matej
and
Ruddat, Helge
2021.
Smoothing toroidal crossing spaces.
Forum of Mathematics, Pi,
Vol. 9,
Issue. ,
Loginov, Konstantin
2022.
On semistable degenerations of Fano varieties.
European Journal of Mathematics,
Vol. 8,
Issue. 3,
p.
991.
Loginov, Konstantin
and
Moraga, Joaquín
2022.
Maximal log Fano manifolds are generalized Bott towers.
Journal of Algebra,
Vol. 612,
Issue. ,
p.
110.


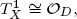 where
where 