Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
McGhee, D.F.
1987.
Generalised multiparameter simple eigenvalues and bifurcation.
Applicable Analysis,
Vol. 25,
Issue. 1-2,
p.
55.
Bari, Rehana
2002.
Local bifurcation theory for multiparameter nonlinear eigenvalue problems.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 48,
Issue. 8,
p.
1077.
2010.
Multiparameter Eigenvalue Problems.
p.
210.


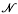 :
: