Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T02:04:27.602Z Has data issue: false hasContentIssue false
  • English
  • Français

Similarité entre l'algèbre de Volterra et un quotient d'algèbre uniforme

Published online by Cambridge University Press:  20 January 2009

Konin Koua
Konin Koua
Affiliation:
Mathématiques et InformatiqueUniversité Bordeaux 1351 Cours de la Libération33405 Talence CedexFrance
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Two commutative Banach algebras A and B are said to be similar if there exists a Banach algebra D such that [xD]− = D for some x in D, and two one-to-one continuous homomorphisms φ:D→A and ψ:D→B such that φ(D) is a dense ideal of A and ψ(D) a dense ideal of B.

We prove in this paper that the Volterra algebra 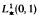is similar to A0/e-z A0 where A0 is the commutative uniform, separable Banach algebra of all continuous functions on the closed right-hand half plane 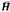, analytic on H and vanishing at infinity. We deduce from this result that multiplication by an element of A0/e-z A0 is a compact mapping.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 34 , Issue 3 , October 1991 , pp. 383 - 391
Copyright
Copyright © Edinburgh Mathematical Society 1991

References

RÉFÉRENCES

1.Boas, R., Entire functions, Pure and Appl. Math. 5 (Academic Press Inc., New York, 1954).Google Scholar
2.Dales, H. G., Automatic continuity: a survey, Bull. London Math. Soc. 10 (1978), 129–183.Google Scholar
3.Esterle, J., Elements for a classification of commutative radical Banach algebras, (Lecture Notes in Math. 975, Springer-Verlag, Berlin, Heidelberg, New York, 1983), 4–65.Google Scholar
4.Esterle, J., Quasimultipliers, representations of H∞ and the closed ideal problem for commutative Banach algebras, (Lecture Notes in Math. 975, Springer-Verlag, Berlin, Heidelberg, New York, 1983), 66–162.Google Scholar
5.Esterle, J., Strouse, E. and Zouakia, F., Theorems of Katznelson-Tzafrini type, J. Fund. Anal. 94 (1990), 273–287.Google Scholar
6.Gelfand, I. M., Raikov, D. A. et Chilov, G. E., Les anneaux normes commutatifs (Monographies internatioanles de mathematiques modernes, Gauthier Villars, Paris, 1964).Google Scholar
7.Sinclair, A. M., Continuous semi-groups in Banach algebras (London Math. Soc. Lee. Notes 63, 1982).Google Scholar
8.Strouse, E., Closed ideals in convolutions algebras and the Laplace transform, Michigan Math. J. 35 (1988), 185–196.Google Scholar