No CrossRef data available.
Published online by Cambridge University Press: 15 November 2024
For 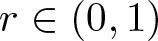 $r\in(0,1)$, let
$r\in(0,1)$, let  $\mu \left( r\right) $ be the modulus of the plane Grötzsch ring
$\mu \left( r\right) $ be the modulus of the plane Grötzsch ring 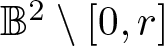 $\mathbb{B}^2\setminus[0,r]$, where
$\mathbb{B}^2\setminus[0,r]$, where 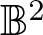 $\mathbb{B}^2$ is the unit disk. In this paper, we prove that
$\mathbb{B}^2$ is the unit disk. In this paper, we prove that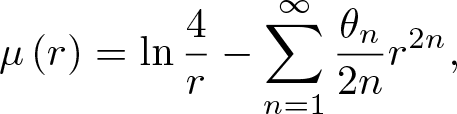 \begin{equation*}\mu \left( r\right) =\ln \frac{4}{r}-\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}r^{2n},\end{equation*}
\begin{equation*}\mu \left( r\right) =\ln \frac{4}{r}-\sum_{n=1}^{\infty }\frac{\theta _{n}}{2n}r^{2n},\end{equation*}
with 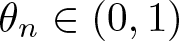 $\theta _{n}\in \left( 0,1\right)$. Employing this series expansion, we obtain several absolutely monotonic and (logarithmically) completely monotonic functions involving
$\theta _{n}\in \left( 0,1\right)$. Employing this series expansion, we obtain several absolutely monotonic and (logarithmically) completely monotonic functions involving 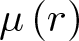 $\mu \left( r\right) $, which yields some new results and extend certain known ones. Moreover, we give an affirmative answer to the conjecture proposed by Alzer and Richards in H. Alzer and K. Richards, On the modulus of the Grötzsch ring, J. Math. Anal. Appl. 432(1): (2015), 134–141, DOI 10.1016/j.jmaa.2015.06.057. As applications, several new sharp bounds and functional inequalities for
$\mu \left( r\right) $, which yields some new results and extend certain known ones. Moreover, we give an affirmative answer to the conjecture proposed by Alzer and Richards in H. Alzer and K. Richards, On the modulus of the Grötzsch ring, J. Math. Anal. Appl. 432(1): (2015), 134–141, DOI 10.1016/j.jmaa.2015.06.057. As applications, several new sharp bounds and functional inequalities for 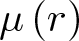 $\mu \left( r\right) $ are established.
$\mu \left( r\right) $ are established.