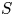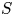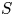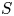1. Introduction
A finiteness condition for a class of universal algebras is a property that is satisfied by at least all finite members of that class. Some of the most important finiteness conditions are ascending chain conditions. The study of ascending chain conditions on ideals of rings, initiated by Noether in the early part of the last century, has been instrumental in the development of the structure theory of rings. A ring is right (respectively left) Noetherian if it satisfies the ascending chain condition on right (respectively left) ideals, and Noetherian if it is both right Noetherian and left Noetherian. Noetherian rings play a key role in many major ring-theoretic results, such as Hilbert's basis theorem and Krull's intersection theorem.
We call a semigroup $S$![]() weakly right noetherian if every right ideal of $S$
weakly right noetherian if every right ideal of $S$![]() is finitely generated.Footnote 1 Similarly, a semigroup is weakly left noetherian if every left ideal is finitely generated. We call a semigroup weakly noetherian if it is both weakly right noetherian and weakly left noetherian. It is clear that each of these properties is a finiteness condition. In this paper, we will focus on weakly right noetherian semigroups. Such semigroups have received a significant amount of attention; see for instance [Reference Aubert1, Reference Davvaz and Nazemian6, Reference Jespers and Okniński14, Reference Satyanarayana26].
is finitely generated.Footnote 1 Similarly, a semigroup is weakly left noetherian if every left ideal is finitely generated. We call a semigroup weakly noetherian if it is both weakly right noetherian and weakly left noetherian. It is clear that each of these properties is a finiteness condition. In this paper, we will focus on weakly right noetherian semigroups. Such semigroups have received a significant amount of attention; see for instance [Reference Aubert1, Reference Davvaz and Nazemian6, Reference Jespers and Okniński14, Reference Satyanarayana26].
Related to the property of being weakly right noetherian is the stronger condition that every right congruence is finitely generated; we call semigroups satisfying this condition right noetherian. Such semigroups were studied systematically in [Reference Miller and Ruškuc21] and had previously been considered in [Reference Hotzel12, Reference Kozhukhov17, Reference Kozhukhov18]. Another related notion is that of the universal right congruence being finitely generated, which was first considered in [Reference Dandan, Gould, Quinn-Gregson and Zenab5]. The stronger condition that every right congruence of finite index is finitely generated (where index means the number of classes) was introduced and studied in [Reference Miller20].
This paper is structured as follows. In § 2, we provide the necessary preliminary material. In § 3, we present some equivalent formulations of the property of being weakly right noetherian. In § 4 and 5, we explore how a semigroup and its substructures and quotients relate to one another with regard to the property of being weakly right noetherian. We then investigate how this property behaves under various semigroup-theoretic constructions in § 6. Specifically, we consider direct products, free products, semilattices of semigroups, Rees matrix semigroups, Brandt extensions and Bruck–Reilly extensions. Section 7 is concerned with regular semigroups. We first consider regular semigroups in general, and then focus on the important subclasses of inverse semigroups and completely regular semigroups. Finally, in § 8, we consider commutative semigroups. The main result of that section is a necessary and sufficient condition for a commutative semigroup with finitely many archimedean components to be weakly noetherian.
2. Preliminaries
In this section, we establish some basic definitions and notation. We begin by providing some set-theoretic definitions.
A relation $\leq$![]() on a set $P$
on a set $P$![]() is said to be preorder if it is both reflexive and transitive. If a preorder is also symmetric, then it is an equivalence relation. On the other hand, if a preorder is antisymmetric then it is a partial order.
is said to be preorder if it is both reflexive and transitive. If a preorder is also symmetric, then it is an equivalence relation. On the other hand, if a preorder is antisymmetric then it is a partial order.
A poset is a set $P$![]() together with a partial order $\leq$
together with a partial order $\leq$![]() . Given any set $X,$
. Given any set $X,$![]() a collection $P$
a collection $P$![]() of subsets of $X$
of subsets of $X$![]() forms a poset under the partial order of inclusion. In particular, the set of all right ideals of a semigroup is a poset (under $\subseteq$
forms a poset under the partial order of inclusion. In particular, the set of all right ideals of a semigroup is a poset (under $\subseteq$![]() ).
).
Let $(P,\, \leq _P)$![]() and $(Q,\, \leq _Q)$
and $(Q,\, \leq _Q)$![]() be two posets. A map $\theta : P\to Q$
be two posets. A map $\theta : P\to Q$![]() is said to be order-preserving if $x\leq _P y$
is said to be order-preserving if $x\leq _P y$![]() implies $x\theta \leq _Q y\theta$
implies $x\theta \leq _Q y\theta$![]() for all $x,\, y\in P.$
for all $x,\, y\in P.$![]() A map $\theta : P\to Q$
A map $\theta : P\to Q$![]() is an isomorphism if both $\theta$
is an isomorphism if both $\theta$![]() and $\theta ^{-1}$
and $\theta ^{-1}$![]() are order-preserving (i.e. $x\leq _P y$
are order-preserving (i.e. $x\leq _P y$![]() if and only if $x\theta \leq _Q y\theta$
if and only if $x\theta \leq _Q y\theta$![]() for all $x,\, y\in P$
for all $x,\, y\in P$![]() ) and $\theta$
) and $\theta$![]() is a bijection. We say that $P$
is a bijection. We say that $P$![]() and $Q$
and $Q$![]() are isomorphic if there exists an isomorphism between them. Note that to show that a map $\theta : P\to Q$
are isomorphic if there exists an isomorphism between them. Note that to show that a map $\theta : P\to Q$![]() is an isomorphism, it suffices to prove that $\theta$
is an isomorphism, it suffices to prove that $\theta$![]() is surjective and that $x\leq _P y$
is surjective and that $x\leq _P y$![]() if and only if $x\theta \leq _Q y\theta$
if and only if $x\theta \leq _Q y\theta$![]() for all $x,\, y\in P$
for all $x,\, y\in P$![]() .
.
Two elements $a$![]() and $b$
and $b$![]() of a poset $P$
of a poset $P$![]() are said to be comparable if either $a\leq b$
are said to be comparable if either $a\leq b$![]() or $b\leq a$
or $b\leq a$![]() ; otherwise, $a$
; otherwise, $a$![]() and $b$
and $b$![]() are incomparable. A subset of $P$
are incomparable. A subset of $P$![]() in which any two elements are comparable is called a chain. An antichain of $P$
in which any two elements are comparable is called a chain. An antichain of $P$![]() is a subset consisting of pairwise incomparable elements.
is a subset consisting of pairwise incomparable elements.
We now turn our attention to semigroups. We refer the reader to [Reference Howie13] for a more comprehensive introduction to semigroup theory. Throughout the remainder of the section, $S$![]() will denote a semigroup.
will denote a semigroup.
We denote by $S^{1}$![]() the monoid obtained from $S$
the monoid obtained from $S$![]() by adjoining an identity if necessary (if $S$
by adjoining an identity if necessary (if $S$![]() is already a monoid, then $S^{1}=S$
is already a monoid, then $S^{1}=S$![]() ). Similarly, we denote by $S^{0}$
). Similarly, we denote by $S^{0}$![]() the semigroup with zero obtained from $S$
the semigroup with zero obtained from $S$![]() by adjoining a zero if necessary.
by adjoining a zero if necessary.
Let $M$![]() be a monoid with identity $1.$
be a monoid with identity $1.$![]() An element $a\in M$
An element $a\in M$![]() is said to be right invertible if there exists $b\in M$
is said to be right invertible if there exists $b\in M$![]() such that $ab=1.$
such that $ab=1.$![]() Left invertible elements are defined dually. An element of $M$
Left invertible elements are defined dually. An element of $M$![]() is called a unit if it is both right invertible and left invertible. The units of $M$
is called a unit if it is both right invertible and left invertible. The units of $M$![]() form a group, called the group of units of $M,$
form a group, called the group of units of $M,$![]() which we denote by $U(M).$
which we denote by $U(M).$![]()
We denote the set of idempotents of $S$![]() by $E(S).$
by $E(S).$![]() If $S=E(S),$
If $S=E(S),$![]() it is called a band. A semilattice is a commutative band. The multiplication in a semilattice $E$
it is called a band. A semilattice is a commutative band. The multiplication in a semilattice $E$![]() induces the following partial order:
induces the following partial order:
In this way, we may view $E$![]() as a meet-semilattice in the order-theoretic sense. Conversely, any order-theoretic meet-semilattice may be viewed as a commutative band with meet taken as the binary operation.
as a meet-semilattice in the order-theoretic sense. Conversely, any order-theoretic meet-semilattice may be viewed as a commutative band with meet taken as the binary operation.
If $a,\, b\in S$![]() are such that $a=aba$
are such that $a=aba$![]() and $b=bab,$
and $b=bab,$![]() then $b$
then $b$![]() is called an inverse of $a.$
is called an inverse of $a.$![]() The semigroup $S$
The semigroup $S$![]() is said to be regular if every element of $S$
is said to be regular if every element of $S$![]() has an inverse. If, additionally, the inverse of each element of $S$
has an inverse. If, additionally, the inverse of each element of $S$![]() is unique, then $S$
is unique, then $S$![]() is an inverse semigroup. It is well known that a semigroup is inverse if and only if it is regular and its idempotents form a semilattice [Reference Howie13, Theorem 5.1.1].
is an inverse semigroup. It is well known that a semigroup is inverse if and only if it is regular and its idempotents form a semilattice [Reference Howie13, Theorem 5.1.1].
A subset $I\subseteq S$![]() is said to be a right ideal of $S$
is said to be a right ideal of $S$![]() if $IS\subseteq I.$
if $IS\subseteq I.$![]() Left ideals are defined dually, and an ideal of $S$
Left ideals are defined dually, and an ideal of $S$![]() is a subset that it is both a right ideal and a left ideal.
is a subset that it is both a right ideal and a left ideal.
Given a subset $X\subseteq S,$![]() the right ideal generated by $X$
the right ideal generated by $X$![]() is the set $XS^{1}.$
is the set $XS^{1}.$![]() A right ideal $I$
A right ideal $I$![]() of $S$
of $S$![]() is said to be finitely generated if it can be generated by a finite set.
is said to be finitely generated if it can be generated by a finite set.
Note that a right ideal of $S$![]() can be generated by a set as a right ideal or as a semigroup. For proper right ideals, we will always use the term ‘generate’ in the former sense. When we say that $S$
can be generated by a set as a right ideal or as a semigroup. For proper right ideals, we will always use the term ‘generate’ in the former sense. When we say that $S$![]() is generated by a set $X,$
is generated by a set $X,$![]() we mean ‘generated as a semigroup’, unless stated otherwise, and we write $S=\langle X\rangle .$
we mean ‘generated as a semigroup’, unless stated otherwise, and we write $S=\langle X\rangle .$![]() We note that a right ideal can be finitely generated as a right ideal but not as a semigroup; e.g. any non-finitely group $G$
We note that a right ideal can be finitely generated as a right ideal but not as a semigroup; e.g. any non-finitely group $G$![]() is certainly finitely generated as a right ideal.
is certainly finitely generated as a right ideal.
A right congruence on $S$![]() is an equivalence relation $\rho$
is an equivalence relation $\rho$![]() on $S$
on $S$![]() such that $(a,\, b)\in \rho$
such that $(a,\, b)\in \rho$![]() implies $(ac,\, bc)\in \rho$
implies $(ac,\, bc)\in \rho$![]() for all $a,\, b,\, c\in S$
for all $a,\, b,\, c\in S$![]() ; left congruences are defined analogously. A congruence is a relation that is both a right congruence and left congruence. For a congruence $\rho$
; left congruences are defined analogously. A congruence is a relation that is both a right congruence and left congruence. For a congruence $\rho$![]() on $S,$
on $S,$![]() we denote the congruence class of an element $a\in S$
we denote the congruence class of an element $a\in S$![]() by $[a]_{\rho }.$
by $[a]_{\rho }.$![]()
Recall that a semigroup is right noetherian if every right congruence is finitely generated. (A right congruence $\rho$![]() on $S$
on $S$![]() is finitely generated if there exists a finite set $X\subseteq \rho$
is finitely generated if there exists a finite set $X\subseteq \rho$![]() such that $\rho$
such that $\rho$![]() is the smallest right congruence on $S$
is the smallest right congruence on $S$![]() containing $X.$
containing $X.$![]() ) Right noetherian semigroups are weakly right noetherian [Reference Miller and Ruškuc21, Lemma 2.7], but the converse certainly does not hold. Indeed, unlike the situation for rings, the lattice of right congruences on a semigroup is not, in general, isomorphic to the lattice of right ideals. For example, groups have no proper right ideals, but the lattice of right congruences on a group is isomorphic to its lattice of subgroups. Consequently, groups are trivially weakly right noetherian, but a group is right noetherian if and only if all its subgroups are finitely generated [Reference Miller and Ruškuc21, Proposition 2.14].
) Right noetherian semigroups are weakly right noetherian [Reference Miller and Ruškuc21, Lemma 2.7], but the converse certainly does not hold. Indeed, unlike the situation for rings, the lattice of right congruences on a semigroup is not, in general, isomorphic to the lattice of right ideals. For example, groups have no proper right ideals, but the lattice of right congruences on a group is isomorphic to its lattice of subgroups. Consequently, groups are trivially weakly right noetherian, but a group is right noetherian if and only if all its subgroups are finitely generated [Reference Miller and Ruškuc21, Proposition 2.14].
The most essential tools for understanding the structure of a semigroup are its Green's relations $\mathcal {L},\, \mathcal {R},\, \mathcal {H},\, \mathcal {D}$![]() and $\mathcal {J}.$
and $\mathcal {J}.$![]() They are defined as follows.
They are defined as follows.
Two elements $a,\, b\in S$![]() are $\mathcal {L}$
are $\mathcal {L}$![]() -related if they generate the same principal left ideal, i.e. $S^{1}a=S^{1}b.$
-related if they generate the same principal left ideal, i.e. $S^{1}a=S^{1}b.$![]() Similarly, two elements $a,\, b\in S$
Similarly, two elements $a,\, b\in S$![]() are $\mathcal {R}$
are $\mathcal {R}$![]() -related if they generate the same principal right ideal. Green's relation $\mathcal {H}$
-related if they generate the same principal right ideal. Green's relation $\mathcal {H}$![]() is defined as $\mathcal {H}=\mathcal {L}\cap \mathcal {R}.$
is defined as $\mathcal {H}=\mathcal {L}\cap \mathcal {R}.$![]() Two elements $a,\, b\in S$
Two elements $a,\, b\in S$![]() are $\mathcal {D}$
are $\mathcal {D}$![]() -related if there exists $c\in S$
-related if there exists $c\in S$![]() such that $a\,\mathcal {L}\,c$
such that $a\,\mathcal {L}\,c$![]() and $c\,\mathcal {R}\,b.$
and $c\,\mathcal {R}\,b.$![]() Finally, if two elements $a,\, b\in S$
Finally, if two elements $a,\, b\in S$![]() generate the same principal ideal (i.e. $S^{1}aS^{1}=S^{1}bS^{1}$
generate the same principal ideal (i.e. $S^{1}aS^{1}=S^{1}bS^{1}$![]() ), then they are said to be $\mathcal {J}$
), then they are said to be $\mathcal {J}$![]() -related.
-related.
It is obvious from the definitions that $\mathcal {L},\, \mathcal {R},\, \mathcal {H}$![]() and $\mathcal {J}$
and $\mathcal {J}$![]() are equivalence relations on $S,$
are equivalence relations on $S,$![]() and it turns out that $\mathcal {D}$
and it turns out that $\mathcal {D}$![]() is also an equivalence relation. Moreover, Green's relation $\mathcal {L}$
is also an equivalence relation. Moreover, Green's relation $\mathcal {L}$![]() is a right congruence on $S$
is a right congruence on $S$![]() and $\mathcal {R}$
and $\mathcal {R}$![]() is a left congruence on $S.$
is a left congruence on $S.$![]()
Green's relation $\mathcal {R}$![]() defines a preorder $\leq _{\mathcal {R}}$
defines a preorder $\leq _{\mathcal {R}}$![]() on $S,$
on $S,$![]() given by
given by
The preorder $\mathcal {R}$![]() induces a partial order on the set of $\mathcal {R}$
induces a partial order on the set of $\mathcal {R}$![]() -classes of $S$
-classes of $S$![]() : $R_a\leq R_b$
: $R_a\leq R_b$![]() if and only if $a\leq _{\mathcal {R}}b.$
if and only if $a\leq _{\mathcal {R}}b.$![]() It is easy to see that the poset of $\mathcal {R}$
It is easy to see that the poset of $\mathcal {R}$![]() -classes of $S$
-classes of $S$![]() is isomorphic to the poset of principal right ideals of $S,$
is isomorphic to the poset of principal right ideals of $S,$![]() via the isomorphism $R_a\mapsto aS^{1}.$
via the isomorphism $R_a\mapsto aS^{1}.$![]() Similarly, one can define preorders $\leq _{\mathcal {L}}$
Similarly, one can define preorders $\leq _{\mathcal {L}}$![]() and $\leq _{\mathcal {J}},$
and $\leq _{\mathcal {J}},$![]() leading to partial orders on the sets of $\mathcal {L}$
leading to partial orders on the sets of $\mathcal {L}$![]() -classes and $\mathcal {J}$
-classes and $\mathcal {J}$![]() -classes, respectively.
-classes, respectively.
Note that when we need to distinguish between Green's relations on different semigroups, we will write them with the semigroup as a subscipt; i.e. $\mathcal {K}_S$![]() stands for $\mathcal {K},$
stands for $\mathcal {K},$![]() where $\mathcal {K}$
where $\mathcal {K}$![]() is any of Green's relations on $S.$
is any of Green's relations on $S.$![]()
It is easy to see that the following inclusions between Green's relations hold:
It can be easily shown that every right (respectively left) ideal is a union of $\mathcal {R}$![]() -classes (respectively $\mathcal {L}$
-classes (respectively $\mathcal {L}$![]() -classes), and every ideal is a union of $\mathcal {J}$
-classes), and every ideal is a union of $\mathcal {J}$![]() -classes. A semigroup with no proper (right) ideals is called (right) simple. A simple semigroup has a single $\mathcal {J}$
-classes. A semigroup with no proper (right) ideals is called (right) simple. A simple semigroup has a single $\mathcal {J}$![]() -class; if it is right simple, then it has a single $\mathcal {R}$
-class; if it is right simple, then it has a single $\mathcal {R}$![]() -class. If $S$
-class. If $S$![]() has a zero $0,$
has a zero $0,$![]() $S^{2}\neq \{0\},$
$S^{2}\neq \{0\},$![]() and $\{0\}$
and $\{0\}$![]() is the only proper ideal of $S,$
is the only proper ideal of $S,$![]() then it is called $0$
then it is called $0$![]() -simple.
-simple.
Given an ideal $I$![]() of $S,$
of $S,$![]() the Rees quotient of $S$
the Rees quotient of $S$![]() by $I,$
by $I,$![]() denoted by $S/I,$
denoted by $S/I,$![]() is the set $(S{\setminus} I)\cup \{0\}$
is the set $(S{\setminus} I)\cup \{0\}$![]() with multiplication given by
with multiplication given by

Let $J$![]() be a $\mathcal {J}$
be a $\mathcal {J}$![]() -class of $S.$
-class of $S.$![]() The principal factor of $J$
The principal factor of $J$![]() is defined as follows. If $J$
is defined as follows. If $J$![]() is the unique minimal ideal of $S,$
is the unique minimal ideal of $S,$![]() called the kernel of $S,$
called the kernel of $S,$![]() its principal factor is itself. Otherwise, the principal factor of $J$
its principal factor is itself. Otherwise, the principal factor of $J$![]() is the Rees quotient of the subsemigroup $S^{1}xS^{1},$
is the Rees quotient of the subsemigroup $S^{1}xS^{1},$![]() where $x$
where $x$![]() is any element of $J,$
is any element of $J,$![]() by the ideal $(S^{1}xS^{1}) {\setminus} J.$
by the ideal $(S^{1}xS^{1}) {\setminus} J.$![]()
The principal factors of $S$![]() are the principal factors of its $\mathcal {J}$
are the principal factors of its $\mathcal {J}$![]() -classes. The kernel of $S,$
-classes. The kernel of $S,$![]() if it exists, is simple; all other principal factors are either $0$
if it exists, is simple; all other principal factors are either $0$![]() -simple or null (every product of two elements equals zero).
-simple or null (every product of two elements equals zero).
A principal series of a semigroup $S$![]() is a finite chain of ideals
is a finite chain of ideals
where $K(S)$![]() is the kernel of $S,$
is the kernel of $S,$![]() and $I_k$
and $I_k$![]() is maximal in $I_{k+1}$
is maximal in $I_{k+1}$![]() for each $i\in \{1,\, \ldots ,\, n-1\}.$
for each $i\in \{1,\, \ldots ,\, n-1\}.$![]() The kernel $K(S)$
The kernel $K(S)$![]() and the Rees quotients $I_{k+1}/I_k$
and the Rees quotients $I_{k+1}/I_k$![]() are the principal factors of $S.$
are the principal factors of $S.$![]()
It is folklore that a semigroup has a principal series of length $n$![]() if and only if it has exactly $n$
if and only if it has exactly $n$![]() $\mathcal {J}$
$\mathcal {J}$![]() -classes.
-classes.
Closely related to the notion of one-sided ideals is that of semigroup acts. We provide some basic definitions about acts; one should consult [Reference Kilp, Knauer and Mikhalev16] for more information.
A (right) $S$![]() -act is a non-empty set $A$
-act is a non-empty set $A$![]() together with a map
together with a map
such that $a(st)=(as)t$![]() for all $a\in A$
for all $a\in A$![]() and $s,\, t\in S.$
and $s,\, t\in S.$![]() (If $S$
(If $S$![]() is a monoid, we also require that $a1=a$
is a monoid, we also require that $a1=a$![]() for all $a\in A$
for all $a\in A$![]() .) For instance, $S$
.) For instance, $S$![]() itself is an $S$
itself is an $S$![]() -act via right multiplication.
-act via right multiplication.
A subset $B$![]() of an $S$
of an $S$![]() -act $A$
-act $A$![]() is a subact of $A$
is a subact of $A$![]() if $bs\in B$
if $bs\in B$![]() for all $b\in B$
for all $b\in B$![]() and $s\in S.$
and $s\in S.$![]() Note that the right ideals of $S$
Note that the right ideals of $S$![]() are precisely the subacts of the $S$
are precisely the subacts of the $S$![]() -act $S.$
-act $S.$![]()
Given an $S$![]() -act $A$
-act $A$![]() and a subact $B$
and a subact $B$![]() of $A,$
of $A,$![]() the Rees quotient of $A$
the Rees quotient of $A$![]() by $B,$
by $B,$![]() denoted by $A/B,$
denoted by $A/B,$![]() is the set $(A {\setminus} B)\cup \{0\}$
is the set $(A {\setminus} B)\cup \{0\}$![]() with action given by
with action given by

and $0\cdot s=0,$![]() for all $a\in A {\setminus} B$
for all $a\in A {\setminus} B$![]() and $s\in S.$
and $s\in S.$![]() It can be easily verified that $A/B$
It can be easily verified that $A/B$![]() is an $S$
is an $S$![]() -act via the above action.
-act via the above action.
A subset $U$![]() of an $S$
of an $S$![]() -act $A$
-act $A$![]() is a generating set for $A$
is a generating set for $A$![]() if $A=US^{1},$
if $A=US^{1},$![]() and $A$
and $A$![]() is said to be finitely generated if it has a finite generating set.
is said to be finitely generated if it has a finite generating set.
We call an $S$![]() -act $A$
-act $A$![]() noetherian if every subact of $A$
noetherian if every subact of $A$![]() is finitely generated; equivalently, $A$
is finitely generated; equivalently, $A$![]() satisfies the ascending chain condition on its subacts. In particular, the $S$
satisfies the ascending chain condition on its subacts. In particular, the $S$![]() -act $S$
-act $S$![]() being noetherian is equivalent to $S$
being noetherian is equivalent to $S$![]() being a weakly right noetherian semigroup.
being a weakly right noetherian semigroup.
3. Equivalent formulations and elementary facts
We begin this section by presenting equivalent characterizations of weakly right noetherian semigroups in terms of the ascending chain condition and maximal condition on right ideals. The proof of this result is essentially the same as that of the analogue for rings and is omitted.
Proposition 3.1 The following are equivalent for a semigroup $S$![]() :
:
(1) $S$
 is weakly right noetherian$;$
is weakly right noetherian$;$
(2) $S$
 satisfies the ascending chain condition on right ideals$;$
satisfies the ascending chain condition on right ideals$;$ that is$,$
that is$,$ every ascending chain $I_1\subseteq I_2\subseteq \cdots$
every ascending chain $I_1\subseteq I_2\subseteq \cdots$ of right ideals of $S$
of right ideals of $S$ eventually terminates$;$
eventually terminates$;$
(3) every non-empty set of right ideals of $S$
 has a maximal element.
has a maximal element.
We now provide characterizations of weakly right noetherian semigroups in terms of their principal right ideals and also in terms of their $\mathcal {R}$![]() -class structure.
-class structure.
Theorem 3.2 The following are equivalent for a semigroup $S:$![]()
(1) $S$
 is weakly right noetherian;
is weakly right noetherian;(2) $S$
 satisfies the ascending chain condition on principal right ideals and contains no infinite antichain of principal right ideals (under $\subseteq$
satisfies the ascending chain condition on principal right ideals and contains no infinite antichain of principal right ideals (under $\subseteq$ ).
).(3) the poset of $\mathcal {R}$
 -classes of $S$
-classes of $S$ contains no infinite strictly ascending chain or infinite antichain.
contains no infinite strictly ascending chain or infinite antichain.
Proof. $(1)\Rightarrow (2).$![]() By Proposition 3.1, $S$
By Proposition 3.1, $S$![]() certainly satisfies the ascending chain condition on principal right ideals. The fact that $S$
certainly satisfies the ascending chain condition on principal right ideals. The fact that $S$![]() contains no infinite antichain of principal right ideal was proven in [Reference Hotzel12, Lemma 1.6], but we provide a proof for completeness.
contains no infinite antichain of principal right ideal was proven in [Reference Hotzel12, Lemma 1.6], but we provide a proof for completeness.
Suppose for a contradiction that there exists an infinite antichain $\{a_iS^{1} : i\in \mathbb {N}\}$![]() of principal right ideals of $S.$
of principal right ideals of $S.$![]() For each $n\in \mathbb {N},$
For each $n\in \mathbb {N},$![]() let $I_n=\{a_1,\, \ldots ,\, a_n\}S^{1}.$
let $I_n=\{a_1,\, \ldots ,\, a_n\}S^{1}.$![]() Suppose that $I_m=I_n$
Suppose that $I_m=I_n$![]() for some $m\leq n.$
for some $m\leq n.$![]() Then $a_n\in a_iS^{1}$
Then $a_n\in a_iS^{1}$![]() for some $i\leq m.$
for some $i\leq m.$![]() It must be the case that $i=m=n,$
It must be the case that $i=m=n,$![]() for otherwise the incomparability of $a_iS^{1}$
for otherwise the incomparability of $a_iS^{1}$![]() and $a_nS^{1}$
and $a_nS^{1}$![]() would be contradicted. But then we have an infinite strictly ascending chain
would be contradicted. But then we have an infinite strictly ascending chain
of right ideals of $S,$![]() contradicting Proposition 3.1.
contradicting Proposition 3.1.
$(2)\Rightarrow (1).$![]() Suppose that $S$
Suppose that $S$![]() is not weakly right noetherian yet the poset of principal right ideals of $S$
is not weakly right noetherian yet the poset of principal right ideals of $S$![]() does satisfy the ascending chain condition. We need to construct an infinite antichain of principal right ideals of $S.$
does satisfy the ascending chain condition. We need to construct an infinite antichain of principal right ideals of $S.$![]()
By Proposition 3.1, there exists an infinite strictly ascending chain
of right ideals of $S.$![]() Choose elements $a_1\in I_1$
Choose elements $a_1\in I_1$![]() and $a_k\in I_k {\setminus} I_{k-1}$
and $a_k\in I_k {\setminus} I_{k-1}$![]() for $k\geq 2.$
for $k\geq 2.$![]() Then certainly $a_kS^{1}$
Then certainly $a_kS^{1}$![]() is not contained in any $a_jS^{1},\, j< k,$
is not contained in any $a_jS^{1},\, j< k,$![]() since $a_jS^{1}\subseteq I_j$
since $a_jS^{1}\subseteq I_j$![]() and $a_k\in I_k {\setminus} I_{j}$
and $a_k\in I_k {\setminus} I_{j}$![]() .
.
Consider the infinite set $\{a_iS^{1} : i\in \mathbb {N}\}$![]() of principal right ideals of $S.$
of principal right ideals of $S.$![]() This set contains a maximal element, say $a_{k_1}S^{1}$
This set contains a maximal element, say $a_{k_1}S^{1}$![]() ; that is, $a_{k_1}S^{1}$
; that is, $a_{k_1}S^{1}$![]() is not contained in any $a_jS^{1},\, j\neq k_1.$
is not contained in any $a_jS^{1},\, j\neq k_1.$![]() Indeed, if this were not the case, then there would exist an infinite strictly ascending chain of principal right ideals of $S,$
Indeed, if this were not the case, then there would exist an infinite strictly ascending chain of principal right ideals of $S,$![]() contradicting the assumption.
contradicting the assumption.
Now consider the infinite set $\{a_iS^{1} : i\geq k_1+1\}.$![]() Again, this set contains a maximal element, say $a_{k_2}S^{1}.$
Again, this set contains a maximal element, say $a_{k_2}S^{1}.$![]() Thus $a_{k_2}S^{1}$
Thus $a_{k_2}S^{1}$![]() is not contained in $a_jS^{1}$
is not contained in $a_jS^{1}$![]() for any $j>k_1,\, j\neq k_2.$
for any $j>k_1,\, j\neq k_2.$![]() In fact, $a_{k_2}S^{1}$
In fact, $a_{k_2}S^{1}$![]() is not contained in $a_jS^{1}$
is not contained in $a_jS^{1}$![]() for any $j\in \mathbb {N} {\setminus} \{k_2\},$
for any $j\in \mathbb {N} {\setminus} \{k_2\},$![]() since, as observed above, $a_{k_2}S^{1}$
since, as observed above, $a_{k_2}S^{1}$![]() is not contained in any $a_jS^{1},\, j< k$
is not contained in any $a_jS^{1},\, j< k$![]() .
.
Continuing this process ad infinitum, we obtain an infinite antichain $\{a_{k_i}S^{1} : i\in \mathbb {N}\}$![]() of principal right ideals of $S,$
of principal right ideals of $S,$![]() as required.
as required.
$(2)\Leftrightarrow (3).$![]() This follows from the fact, established in § 2, that the poset of $\mathcal {R}$
This follows from the fact, established in § 2, that the poset of $\mathcal {R}$![]() -classes of $S$
-classes of $S$![]() is isomorphic to the poset of principal right ideals of $S$
is isomorphic to the poset of principal right ideals of $S$![]() .
.
Corollary 3.3 Any semigroup with finitely many $\mathcal {R}$![]() -classes is weakly right noetherian. In particular, all finite semigroups and all right simple semigroups (which include groups) are weakly right noetherian.
-classes is weakly right noetherian. In particular, all finite semigroups and all right simple semigroups (which include groups) are weakly right noetherian.
Remark 3.4 The condition that every (two-sided) ideal of a semigroup $S$![]() is finitely generated has been considered in [Reference Aubert1, Reference Kehayopulu and Tsingelis15]. By an argument essentially the same as the proof of Theorem 3.2, this condition is equivalent to $S$
is finitely generated has been considered in [Reference Aubert1, Reference Kehayopulu and Tsingelis15]. By an argument essentially the same as the proof of Theorem 3.2, this condition is equivalent to $S$![]() satisfying the ascending chain condition on principal ideals and containing no infinite antichain of principal ideals, and also to $S$
satisfying the ascending chain condition on principal ideals and containing no infinite antichain of principal ideals, and also to $S$![]() containing no infinite strictly ascending chain or infinite antichain of $\mathcal {J}$
containing no infinite strictly ascending chain or infinite antichain of $\mathcal {J}$![]() -classes. Any weakly right noetherian semigroup satisfies this condition (since every ideal is a one-sided ideal), but the converse does not hold. Indeed, any simple semigroup trivially satisfies the condition that every ideal is finitely generated, but there exist simple semigroups that are not right noetherian; e.g. any completely simple semigroup with infinitely many $\mathcal {R}$
-classes. Any weakly right noetherian semigroup satisfies this condition (since every ideal is a one-sided ideal), but the converse does not hold. Indeed, any simple semigroup trivially satisfies the condition that every ideal is finitely generated, but there exist simple semigroups that are not right noetherian; e.g. any completely simple semigroup with infinitely many $\mathcal {R}$![]() -classes (see Corollary 6.21).
-classes (see Corollary 6.21).
The following result shows that there exist semigroups that satisfy the ascending chain condition on principal right ideals but are not weakly right noetherian.
Proposition 3.5 Let $X$![]() be a non-empty set. Then the free semigroup $F_X$
be a non-empty set. Then the free semigroup $F_X$![]() on $X$
on $X$![]() satisfies the ascending chain condition on principal right ideals. However, $F_X$
satisfies the ascending chain condition on principal right ideals. However, $F_X$![]() is weakly right noetherian if and only if $|X|=1.$
is weakly right noetherian if and only if $|X|=1.$![]()
Proof. Consider two elements $u,\, v\in F_X.$![]() Clearly, $uF_X^{1}\subsetneq vF_X^{1}$
Clearly, $uF_X^{1}\subsetneq vF_X^{1}$![]() if and only if $v$
if and only if $v$![]() is a proper prefix of $u,$
is a proper prefix of $u,$![]() in which case $|u|>|v|.$
in which case $|u|>|v|.$![]() It follows that there cannot exist an infinite strictly ascending chain of principal right ideals of $F_X$
It follows that there cannot exist an infinite strictly ascending chain of principal right ideals of $F_X$![]() .
.
If $|X|=1,$![]() then clearly $F_X\cong \mathbb {N}$
then clearly $F_X\cong \mathbb {N}$![]() contains no incomparable elements, so it is weakly right noetherian by Theorem 3.2.
contains no incomparable elements, so it is weakly right noetherian by Theorem 3.2.
Suppose $|X|\geq 2,$![]() and choose distinct elements $x,\, y\in X.$
and choose distinct elements $x,\, y\in X.$![]() For $i\neq j,$
For $i\neq j,$![]() the element $x^{i}y$
the element $x^{i}y$![]() is not a prefix of $x^{j}y,$
is not a prefix of $x^{j}y,$![]() so $F_X$
so $F_X$![]() contains an infinite antichain $\{(x^{i}y)F_X^{1} : i\in \mathbb {N}\}$
contains an infinite antichain $\{(x^{i}y)F_X^{1} : i\in \mathbb {N}\}$![]() of principal right ideals. Hence, $F_X$
of principal right ideals. Hence, $F_X$![]() is not weakly right noetherian by Theorem 3.2.
is not weakly right noetherian by Theorem 3.2.
Remark 3.6 We can readily deduce from Proposition 3.5 that the property of being weakly right noetherian is not closed under subsemigroups. Indeed, the free semigroup $F_X$![]() is a subsemigroup of the free group on $X,$
is a subsemigroup of the free group on $X,$![]() which is certainly weakly right noetherian.
which is certainly weakly right noetherian.
Monoid acts play the analogous role in the theory of monoids to that of modules in the theory of rings. It is well known that a ring $R$![]() is right Noetherian if and only if every finitely generated right $R$
is right Noetherian if and only if every finitely generated right $R$![]() -module is Noetherian (i.e. it satisfies the ascending chain condition on its submodules) [Reference Goodearl and Warfield8, Corollary 1.4]. We now present the analogue of this result for monoid acts.
-module is Noetherian (i.e. it satisfies the ascending chain condition on its submodules) [Reference Goodearl and Warfield8, Corollary 1.4]. We now present the analogue of this result for monoid acts.
Proposition 3.7 The following are equivalent for a monoid $M$![]() :
:
(1) $M$
 is weakly right noetherian;
is weakly right noetherian;(2) every finitely generated right $M$
 -act is noetherian.
-act is noetherian.
Proof. $(1)\Rightarrow (2)$![]() . Let $A$
. Let $A$![]() be a right $M$
be a right $M$![]() -act with a finite generating set $X,$
-act with a finite generating set $X,$![]() and let $B$
and let $B$![]() be a subact of $A.$
be a subact of $A.$![]() For each $x\in X,$
For each $x\in X,$![]() we define a set
we define a set
Let $X^{\prime }$![]() be the set of elements in $X$
be the set of elements in $X$![]() such that $I_x\neq \emptyset .$
such that $I_x\neq \emptyset .$![]() Since $B$
Since $B$![]() is a subact of $A,$
is a subact of $A,$![]() we have that $I_x$
we have that $I_x$![]() is a right ideal of $S$
is a right ideal of $S$![]() for each $x\in X^{\prime }.$
for each $x\in X^{\prime }.$![]() Since $M$
Since $M$![]() is weakly right noetherian, for each $x\in X^{\prime }$
is weakly right noetherian, for each $x\in X^{\prime }$![]() there exists a finite set $U_x\subseteq I_x$
there exists a finite set $U_x\subseteq I_x$![]() such that $I_x=U_xM.$
such that $I_x=U_xM.$![]() We claim that $B$
We claim that $B$![]() is generated by the set
is generated by the set
Indeed, let $b\in B.$![]() Since $b\in A,$
Since $b\in A,$![]() we have that $b=xm$
we have that $b=xm$![]() for some $x\in X$
for some $x\in X$![]() and $m\in M.$
and $m\in M.$![]() Now $m\in I_x,$
Now $m\in I_x,$![]() so $m=un$
so $m=un$![]() for some $u\in U_x$
for some $u\in U_x$![]() and $n\in M,$
and $n\in M,$![]() and hence $b=(xu)n\in UM.$
and hence $b=(xu)n\in UM.$![]()
$(2)\Rightarrow (1)$![]() . This follows from the fact that the right ideals of $M$
. This follows from the fact that the right ideals of $M$![]() are subacts of the cyclic right $M$
are subacts of the cyclic right $M$![]() -act $M.$
-act $M.$![]()
For commutative semigroups, clearly the properties of being weakly right noetherian and being weakly left noetherian coincide. It is a well-known result, due to Rédei [Reference Rédei24], that every congruence on a finitely generated commutative semigroup is finitely generated; that is:
Theorem 3.8 Rédei [Reference Rédei24]
Every finitely generated commutative semigroup is noetherian $($![]() and hence weakly noetherian$)$
and hence weakly noetherian$)$![]() .
.
In the remainder of this section, we state some useful facts about weakly right noetherian semigroups. The following lemma is well known and will be used repeatedly throughout the remainder of the paper, usually without explicit mention.
Lemma 3.9 Let $S$![]() be a semigroup and let $X$
be a semigroup and let $X$![]() be a subset of $S.$
be a subset of $S.$![]() If the right ideal $XS^{1}$
If the right ideal $XS^{1}$![]() of $S$
of $S$![]() is finitely generated$,$
is finitely generated$,$![]() then there exists a finite subset $Y\subseteq X$
then there exists a finite subset $Y\subseteq X$![]() such that $XS^{1}=YS^{1}.$
such that $XS^{1}=YS^{1}.$![]()
Let $S$![]() be a semigroup. An element $s\in S$
be a semigroup. An element $s\in S$![]() is said to be decomposable if $s\in S^{2}.$
is said to be decomposable if $s\in S^{2}.$![]() An element is indecomposable if it is not decomposable.
An element is indecomposable if it is not decomposable.
Lemma 3.10 Let $S$![]() be a weakly right noetherian semigroup. Then $S$
be a weakly right noetherian semigroup. Then $S$![]() has only finitely many indecomposable elements.
has only finitely many indecomposable elements.
Proof. Since $S$![]() is weakly right noetherian, $S$
is weakly right noetherian, $S$![]() is finitely generated as a right ideal; that is, there exists a finite set $X\subseteq S$
is finitely generated as a right ideal; that is, there exists a finite set $X\subseteq S$![]() such that $S=XS^{1}.$
such that $S=XS^{1}.$![]() Therefore, we have that $S {\setminus} X\subseteq S^{2},$
Therefore, we have that $S {\setminus} X\subseteq S^{2},$![]() so $S$
so $S$![]() has at most $|X|$
has at most $|X|$![]() indecomposable elements.
indecomposable elements.
We now show that a semigroup composed of a finite union of weakly right noetherian subsemigroups is also weakly right noetherian.
Lemma 3.11 Let $S$![]() be a semigroup, and suppose that $S$
be a semigroup, and suppose that $S$![]() is a union of subsemigroups $S_1,\, \ldots ,\, S_n.$
is a union of subsemigroups $S_1,\, \ldots ,\, S_n.$![]() If each $S_i$
If each $S_i$![]() is weakly right noetherian, then $S$
is weakly right noetherian, then $S$![]() is also weakly right noetherian.
is also weakly right noetherian.
Proof. Let $I$![]() be a right ideal of $S.$
be a right ideal of $S.$![]() For $j\in \{1,\, \ldots ,\, n\}$
For $j\in \{1,\, \ldots ,\, n\}$![]() , let $I_j$
, let $I_j$![]() be the restriction of $I$
be the restriction of $I$![]() to $S_j.$
to $S_j.$![]() Then $I_j$
Then $I_j$![]() is a right ideal of $S_j.$
is a right ideal of $S_j.$![]() Since $S_j$
Since $S_j$![]() is weakly right noetherian, $I_j$
is weakly right noetherian, $I_j$![]() is generated by some finite set $X_j.$
is generated by some finite set $X_j.$![]() We claim that $I$
We claim that $I$![]() is generated by the finite set $X=\bigcup _{i=1}^{n}X_i.$
is generated by the finite set $X=\bigcup _{i=1}^{n}X_i.$![]() Indeed, if $a\in I,$
Indeed, if $a\in I,$![]() then $a\in I_j=X_jS_j^{1}$
then $a\in I_j=X_jS_j^{1}$![]() for some $j\in \{1,\, \ldots ,\, n\}.$
for some $j\in \{1,\, \ldots ,\, n\}.$![]()
4. Quotients and ideals
In this section, we consider the relationship between a semigroup and its quotients and ideals with regard to the property of being weakly right noetherian. We first show that this property is closed under quotients (or, equivalently, homomorphic images).
Lemma 4.1 Let $S$![]() be a semigroup and let $\rho$
be a semigroup and let $\rho$![]() be a congruence on $S.$
be a congruence on $S.$![]() If $S$
If $S$![]() is weakly right noetherian, then so is $S/\rho .$
is weakly right noetherian, then so is $S/\rho .$![]()
Proof. Let $I$![]() be a right ideal of $S/\rho ,$
be a right ideal of $S/\rho ,$![]() and define a set
and define a set
It is clear that $J$![]() is a right ideal of $S.$
is a right ideal of $S.$![]() Since $S$
Since $S$![]() is weakly right noetherian, $J$
is weakly right noetherian, $J$![]() is generated by a finite set $X.$
is generated by a finite set $X.$![]() We claim that $\rho$
We claim that $\rho$![]() is generated by the finite set $Y=\{[x]_{\rho } : x\in X\}.$
is generated by the finite set $Y=\{[x]_{\rho } : x\in X\}.$![]() Indeed, let $u\in I.$
Indeed, let $u\in I.$![]() Select $a\in S$
Select $a\in S$![]() such that $[a]_{\rho }=u.$
such that $[a]_{\rho }=u.$![]() Then $a=xs$
Then $a=xs$![]() for some $x\in X$
for some $x\in X$![]() and $s\in S^{1}.$
and $s\in S^{1}.$![]() If $s=1,$
If $s=1,$![]() then $u=[x]_{\rho }\in Y.$
then $u=[x]_{\rho }\in Y.$![]() Otherwise, we have $u=[x]_{\rho }[s]_{\rho }\in Y(S/\rho ),$
Otherwise, we have $u=[x]_{\rho }[s]_{\rho }\in Y(S/\rho ),$![]() as required.
as required.
Remark 4.2 The converse of Lemma 4.1 does not hold. Indeed, the free semigroup $F_X$![]() with $|X|\geq 2$
with $|X|\geq 2$![]() is not weakly right noetherian by Proposition 3.5, but there certainly exist quotients of $F_X$
is not weakly right noetherian by Proposition 3.5, but there certainly exist quotients of $F_X$![]() that are weakly right noetherian.
that are weakly right noetherian.
If $\rho$![]() is a congruence contained in $\mathcal {R},$
is a congruence contained in $\mathcal {R},$![]() then the converse of Lemma 4.1 holds. In fact, we have:
then the converse of Lemma 4.1 holds. In fact, we have:
Lemma 4.3 Let $S$![]() be a semigroup and let $\rho \subseteq \mathcal {R}$
be a semigroup and let $\rho \subseteq \mathcal {R}$![]() be a congruence on $S.$
be a congruence on $S.$![]() Then the poset of $\mathcal {R}$
Then the poset of $\mathcal {R}$![]() -classes of $S$
-classes of $S$![]() is isomorphic to the poset of $\mathcal {R}$
is isomorphic to the poset of $\mathcal {R}$![]() -classes of $S/\rho .$
-classes of $S/\rho .$![]() In particular, $S$
In particular, $S$![]() is weakly right noetherian if and only if $S/\rho$
is weakly right noetherian if and only if $S/\rho$![]() is weakly right noetherian.
is weakly right noetherian.
Proof. Let $P$![]() be the poset of principal right ideals of $S,$
be the poset of principal right ideals of $S,$![]() and let $Q$
and let $Q$![]() be the poset of principal right ideals of $S/\rho .$
be the poset of principal right ideals of $S/\rho .$![]() Since the poset of principal right ideals of a semigroup is isomorphic to the poset of $\mathcal {R}$
Since the poset of principal right ideals of a semigroup is isomorphic to the poset of $\mathcal {R}$![]() -classes, it suffices to prove that $P$
-classes, it suffices to prove that $P$![]() and $Q$
and $Q$![]() are isomorphic. It then follows from Theorem 3.2 that $S$
are isomorphic. It then follows from Theorem 3.2 that $S$![]() is weakly right noetherian if and only if $S/\rho$
is weakly right noetherian if and only if $S/\rho$![]() is weakly right noetherian.
is weakly right noetherian.
Define a map $\theta : P\to Q,\, aS^{1}\mapsto [a]_{\rho }(S/\rho )^{1}.$![]() Clearly, $\theta$
Clearly, $\theta$![]() is surjective, so we just need to show that $aS^{1}\subseteq bS^{1}$
is surjective, so we just need to show that $aS^{1}\subseteq bS^{1}$![]() if and only if $[a]_{\rho }(S/\rho )^{1}\leq [b]_{\rho }(S/\rho )^{1}.$
if and only if $[a]_{\rho }(S/\rho )^{1}\leq [b]_{\rho }(S/\rho )^{1}.$![]() It is clear that the forward direction holds. Conversely, if $[a]_{\rho }(S/\rho )^{1}\subseteq [b]_{\rho }(S/\rho )^{1}$
It is clear that the forward direction holds. Conversely, if $[a]_{\rho }(S/\rho )^{1}\subseteq [b]_{\rho }(S/\rho )^{1}$![]() then $[a]_{\rho }=[b]_{\rho }u$
then $[a]_{\rho }=[b]_{\rho }u$![]() for some $u\in (S/\rho )^{1}.$
for some $u\in (S/\rho )^{1}.$![]() If $u=1,$
If $u=1,$![]() then $(a,\, b)\in \rho \subseteq \mathcal {R},$
then $(a,\, b)\in \rho \subseteq \mathcal {R},$![]() so $aS^{1}=bS^{1}.$
so $aS^{1}=bS^{1}.$![]() If $u\in S/\rho ,$
If $u\in S/\rho ,$![]() then $u=[s]_{\rho }$
then $u=[s]_{\rho }$![]() for some $s\in S.$
for some $s\in S.$![]() Then $(a,\, bs)\in \rho \subseteq \mathcal {R},$
Then $(a,\, bs)\in \rho \subseteq \mathcal {R},$![]() so $aS^{1}=(bs)S^{1}\subseteq bS^{1},$
so $aS^{1}=(bs)S^{1}\subseteq bS^{1},$![]() as required.
as required.
The following question naturally arises from Lemma 4.3.
Open Problem 4.4 Given a semigroup $S$![]() and congruence $\rho$
and congruence $\rho$![]() on $S,$
on $S,$![]() what is the relationship between the poset of $\mathcal {R}$
what is the relationship between the poset of $\mathcal {R}$![]() -classes of $S$
-classes of $S$![]() and the poset of $\mathcal {R}$
and the poset of $\mathcal {R}$![]() -classes of $S/\rho$
-classes of $S/\rho$![]() ?
?
Remark 4.5 It is natural to wonder whether certain results about weakly right noetherian semigroups, such as Theorem 3.2 and Lemma 4.1, can be derived from more general results about posets. In particular, inspired by Theorem 3.2, one could investigate the finiteness condition that a poset contains no infinite ascending chain or infinite antichain. For instance, is this condition closed under homomorphic images?
The next result states that if a right ideal $I$![]() of a semigroup $S$
of a semigroup $S$![]() is weakly right noetherian and the Rees quotient of the $S$
is weakly right noetherian and the Rees quotient of the $S$![]() -act $S$
-act $S$![]() by $I$
by $I$![]() (where $I$
(where $I$![]() is regarded as a subact of $S$
is regarded as a subact of $S$![]() ) is noetherian, then $S$
) is noetherian, then $S$![]() is weakly right noetherian.
is weakly right noetherian.
Proposition 4.6 Let $S$![]() be a semigroup and let $I$
be a semigroup and let $I$![]() be a right ideal of $S.$
be a right ideal of $S.$![]() If $I$
If $I$![]() is weakly right noetherian and $S/I$
is weakly right noetherian and $S/I$![]() is noetherian (as an $S$
is noetherian (as an $S$![]() -act), then $S$
-act), then $S$![]() is weakly right noetherian.
is weakly right noetherian.
Proof. Let $J$![]() be a right ideal of $S.$
be a right ideal of $S.$![]() Suppose first that $I\cap J=\emptyset .$
Suppose first that $I\cap J=\emptyset .$![]() Then $J\subseteq S {\setminus} I$
Then $J\subseteq S {\setminus} I$![]() and $J$
and $J$![]() may be viewed as a subact of $S/I.$
may be viewed as a subact of $S/I.$![]() Since $S/I$
Since $S/I$![]() is noetherian, there exists a finite set $U\subseteq I$
is noetherian, there exists a finite set $U\subseteq I$![]() such that $J=US^{1}.$
such that $J=US^{1}.$![]() Thus $J$
Thus $J$![]() is finitely generated as a right ideal of $S.$
is finitely generated as a right ideal of $S.$![]()
Now suppose that $I\cap J\neq \emptyset .$![]() Then $I\cap J$
Then $I\cap J$![]() is a right ideal of $I.$
is a right ideal of $I.$![]() Since $I$
Since $I$![]() is weakly right noetherian, $I\cap J$
is weakly right noetherian, $I\cap J$![]() is generated by some finite set $X.$
is generated by some finite set $X.$![]() Considering $J$
Considering $J$![]() as an $S$
as an $S$![]() -act, the Rees quotient $A=J/(I\cap J)$
-act, the Rees quotient $A=J/(I\cap J)$![]() is a subact of $S/I.$
is a subact of $S/I.$![]() Since $S/I$
Since $S/I$![]() is noetherian, there exists a finite set $Y\subseteq A$
is noetherian, there exists a finite set $Y\subseteq A$![]() such that $A=YS^{1}.$
such that $A=YS^{1}.$![]() Let $Y^{\prime }=Y {\setminus} \{0\}.$
Let $Y^{\prime }=Y {\setminus} \{0\}.$![]() We claim that $J=(X\cup Y^{\prime })S^{1}.$
We claim that $J=(X\cup Y^{\prime })S^{1}.$![]()
Indeed, let $a\in J.$![]() If $a\in I,$
If $a\in I,$![]() then $a\in X(I\cap J)^{1}.$
then $a\in X(I\cap J)^{1}.$![]() If $a\in J {\setminus} I,$
If $a\in J {\setminus} I,$![]() then $a\in A,$
then $a\in A,$![]() so $a=ys$
so $a=ys$![]() for some $y\in Y$
for some $y\in Y$![]() and $s\in S^{1}.$
and $s\in S^{1}.$![]() Since $a\in S {\setminus} I,$
Since $a\in S {\setminus} I,$![]() we must have $y\in Y^{\prime }.$
we must have $y\in Y^{\prime }.$![]() In either case, we have $a\in (X\cup Y^{\prime })S^{1},$
In either case, we have $a\in (X\cup Y^{\prime })S^{1},$![]() as required.
as required.
Corollary 4.7 Let $S$![]() be a semigroup and let $I$
be a semigroup and let $I$![]() be an ideal of $S$
be an ideal of $S$![]() . If both $I$
. If both $I$![]() and the Rees quotient $S/I$
and the Rees quotient $S/I$![]() are weakly right noetherian, then $S$
are weakly right noetherian, then $S$![]() is weakly right noetherian.
is weakly right noetherian.
Proof. We shall prove that $S/I,$![]() viewed as the Rees quotient of the $S$
viewed as the Rees quotient of the $S$![]() -act $S$
-act $S$![]() by the subact $I,$
by the subact $I,$![]() is a noetherian $S$
is a noetherian $S$![]() -act. It then follows from Proposition 4.6 that $S$
-act. It then follows from Proposition 4.6 that $S$![]() is weakly right noetherian.
is weakly right noetherian.
So, let $A$![]() be a subact of $S/I.$
be a subact of $S/I.$![]() We need to prove that $A$
We need to prove that $A$![]() is finitely generated. Fix an element $z\in I.$
is finitely generated. Fix an element $z\in I.$![]() We claim that $A$
We claim that $A$![]() is a right ideal of $S/I$
is a right ideal of $S/I$![]() (considered as a semigroup). Indeed, let $a\in A$
(considered as a semigroup). Indeed, let $a\in A$![]() and $u\in S/I.$
and $u\in S/I.$![]() If $a,\, u\in S {\setminus} I,$
If $a,\, u\in S {\setminus} I,$![]() then $au\in A$
then $au\in A$![]() since $A$
since $A$![]() is a subact of $S/I.$
is a subact of $S/I.$![]() Otherwise, we have $a=0$
Otherwise, we have $a=0$![]() or $u=0,$
or $u=0,$![]() in which case $au=0\in A.$
in which case $au=0\in A.$![]() (Since $A$
(Since $A$![]() is a subact of $S/I,$
is a subact of $S/I,$![]() we have $0=a\cdot z\in A.$
we have $0=a\cdot z\in A.$![]() ) Since $S$
) Since $S$![]() is weakly right noetherian, there exists a finite set $X\subseteq A$
is weakly right noetherian, there exists a finite set $X\subseteq A$![]() such that $A=X(S/I)^{1}.$
such that $A=X(S/I)^{1}.$![]() We claim that $A=XS^{1}.$
We claim that $A=XS^{1}.$![]() Indeed, if $a\in A,$
Indeed, if $a\in A,$![]() then $a=xu$
then $a=xu$![]() for some $x\in X$
for some $x\in X$![]() and $u\in (S/I)^{1}.$
and $u\in (S/I)^{1}.$![]() If $a\in S^{1} {\setminus} I,$
If $a\in S^{1} {\setminus} I,$![]() then $u\in S^{1} {\setminus} I.$
then $u\in S^{1} {\setminus} I.$![]() Otherwise, $a=0=xz.$
Otherwise, $a=0=xz.$![]() This completes the proof.
This completes the proof.
Recall that in a semigroup $S$![]() with a principal series $K(S)=I_1\subseteq \cdots \subseteq I_n=S,$
with a principal series $K(S)=I_1\subseteq \cdots \subseteq I_n=S,$![]() the kernel $K(S)$
the kernel $K(S)$![]() and the Rees quotients $I_{k+1}/I_k$
and the Rees quotients $I_{k+1}/I_k$![]() are the principal factors of $S.$
are the principal factors of $S.$![]() Therefore, if all the principal factors are weakly right noetherian, then by successively applying Corollary 4.7, we deduce that $S$
Therefore, if all the principal factors are weakly right noetherian, then by successively applying Corollary 4.7, we deduce that $S$![]() is weakly right noetherian.
is weakly right noetherian.
Corollary 4.8 Let $S$![]() be a semigroup with a principal series. If all the principal factors of $S$
be a semigroup with a principal series. If all the principal factors of $S$![]() are weakly right noetherian$,$
are weakly right noetherian$,$![]() then $S$
then $S$![]() is weakly right noetherian.
is weakly right noetherian.
Although ideals of weakly right noetherian semigroup are not in general weakly right noetherian (see, for instance, Example 8.3), they do satisfy the ascending chain condition on principal right ideals. In fact, we prove a stronger statement:
Proposition 4.9 Let $S$![]() be a semigroup and let $I$
be a semigroup and let $I$![]() be an ideal of $S.$
be an ideal of $S.$![]() If $S$
If $S$![]() satisfies the ascending chain condition on principal right ideals$,$
satisfies the ascending chain condition on principal right ideals$,$![]() then so does $I.$
then so does $I.$![]()
Proof. Consider an infinite ascending chain
of principal right ideals of $I.$![]() Then for each $i,\, j\in \mathbb {N}$
Then for each $i,\, j\in \mathbb {N}$![]() with $i< j,$
with $i< j,$![]() there exists $u_{i,j}\in I^{1}$
there exists $u_{i,j}\in I^{1}$![]() such that $a_i=a_{j}u_{i,j}.$
such that $a_i=a_{j}u_{i,j}.$![]() Clearly, we have an infinite ascending chain
Clearly, we have an infinite ascending chain
of principal right ideals of $S.$![]() By assumption, there exists $n\in \mathbb {N}$
By assumption, there exists $n\in \mathbb {N}$![]() such that $a_mS^{1}=a_nS^{1}$
such that $a_mS^{1}=a_nS^{1}$![]() for all $m\geq n.$
for all $m\geq n.$![]() Let $m>n.$
Let $m>n.$![]() If $u_{n,m}=1,$
If $u_{n,m}=1,$![]() then $a_n=a_m.$
then $a_n=a_m.$![]() Now suppose that $u_{n,m}\in I.$
Now suppose that $u_{n,m}\in I.$![]() There exists $s_m\in S^{1}$
There exists $s_m\in S^{1}$![]() such that $a_m=a_ns_m,$
such that $a_m=a_ns_m,$![]() and hence
and hence
We have that $s_mu_{n,m}s_m\in I$![]() since $I$
since $I$![]() is an ideal, so $a_m\in a_nI.$
is an ideal, so $a_m\in a_nI.$![]() Since $a_nI^{1}\subseteq a_mI^{1},$
Since $a_nI^{1}\subseteq a_mI^{1},$![]() we conclude that $a_nI^{1}=a_mI^{1}.$
we conclude that $a_nI^{1}=a_mI^{1}.$![]() Since $m$
Since $m$![]() was chosen arbitrarily, we have shown that the above ascending chain of principal right ideals of $I$
was chosen arbitrarily, we have shown that the above ascending chain of principal right ideals of $I$![]() terminates at $a_nI^{1}.$
terminates at $a_nI^{1}.$![]()
5. Subsemigroups
As mentioned previously, subsemigroups of weakly right noetherian semigroups need not be weakly right noetherian themselves. In this section, we explore various situations in which the property of being weakly right noetherian passes from a semigroup $S$![]() to a subsemigroup $T,$
to a subsemigroup $T,$![]() and vice versa.
and vice versa.
Lemma 5.1 Let $S$![]() be a semigroup, and let $T$
be a semigroup, and let $T$![]() be a subsemigroup of $S$
be a subsemigroup of $S$![]() such that $S {\setminus} T$
such that $S {\setminus} T$![]() is contained in a finite union of $\mathcal {R}$
is contained in a finite union of $\mathcal {R}$![]() -classes. If $T$
-classes. If $T$![]() is weakly right noetherian, then $S$
is weakly right noetherian, then $S$![]() is weakly right noetherian.
is weakly right noetherian.
Proof. Let $I$![]() be a right ideal of $S.$
be a right ideal of $S.$![]() Then $I\cap T$
Then $I\cap T$![]() is a right ideal of $T.$
is a right ideal of $T.$![]() Since $T$
Since $T$![]() is weakly right noetherian, there exists a finite set $X\subseteq I\cap T$
is weakly right noetherian, there exists a finite set $X\subseteq I\cap T$![]() such that $I\cap T=XT^{1}.$
such that $I\cap T=XT^{1}.$![]()
Let $R_1,\, \ldots ,\, R_n$![]() be the $\mathcal {R}$
be the $\mathcal {R}$![]() -classes that intersect with $S {\setminus} T.$
-classes that intersect with $S {\setminus} T.$![]() For each $i\in \{1,\, \ldots \, n\},$
For each $i\in \{1,\, \ldots \, n\},$![]() fix $r_i\in R_i.$
fix $r_i\in R_i.$![]() It is easy to see that if $I$
It is easy to see that if $I$![]() intersects an $\mathcal {R}$
intersects an $\mathcal {R}$![]() -class $R,$
-class $R,$![]() then $R\subseteq I.$
then $R\subseteq I.$![]() We claim that $I$
We claim that $I$![]() is generated by the finite set
is generated by the finite set
Indeed, let $a\in I.$![]() If $a\in T,$
If $a\in T,$![]() then $a\in I\cap T=XT^{1}.$
then $a\in I\cap T=XT^{1}.$![]() If $a\in S {\setminus} T,$
If $a\in S {\setminus} T,$![]() then $a=r_is$
then $a=r_is$![]() for some $i\in \{1,\, \ldots \, n\}$
for some $i\in \{1,\, \ldots \, n\}$![]() and $s\in S^{1}.$
and $s\in S^{1}.$![]() Hence, in either case, we have that $a\in YS^{1}.$
Hence, in either case, we have that $a\in YS^{1}.$![]()
Remark 5.2 The converse of Lemma 5.1 does not hold. Indeed, in Remark 6.10, an example is provided of a weakly right noetherian semigroup $S$![]() with a subsemigroup $T$
with a subsemigroup $T$![]() such that $S {\setminus} T$
such that $S {\setminus} T$![]() is a group and $T$
is a group and $T$![]() is not weakly right noetherian.
is not weakly right noetherian.
In [Reference Wallace27], Wallace introduced the idea of Greens’ relations taken relative to a subsemigroup. Let $S$![]() be a semigroup and let $T$
be a semigroup and let $T$![]() be a subsemigroup of $S.$
be a subsemigroup of $S.$![]() The $T$
The $T$![]() -relative Green's relation $\mathcal {R}^{T}$
-relative Green's relation $\mathcal {R}^{T}$![]() on $S$
on $S$![]() is given by
is given by
The relation $\mathcal {L}^{T}$![]() is defined dually, and $\mathcal {H}^{T}=\mathcal {R}^{T}\cap \mathcal {L}^{T}.$
is defined dually, and $\mathcal {H}^{T}=\mathcal {R}^{T}\cap \mathcal {L}^{T}.$![]() The relations $\mathcal {D}^{T}$
The relations $\mathcal {D}^{T}$![]() and $\mathcal {J}^{T}$
and $\mathcal {J}^{T}$![]() are defined in a similar way. All of these relations are equivalence relations on $S,$
are defined in a similar way. All of these relations are equivalence relations on $S,$![]() and they respect $T$
and they respect $T$![]() in the sense that each class lies entirely in $T$
in the sense that each class lies entirely in $T$![]() or entirely in $S {\setminus} T.$
or entirely in $S {\setminus} T.$![]() The subsemigroup $T$
The subsemigroup $T$![]() is said to have finite Green index in $S$
is said to have finite Green index in $S$![]() if there are only finitely many $\mathcal {H}^{T}$
if there are only finitely many $\mathcal {H}^{T}$![]() -classes in $S {\setminus} T.$
-classes in $S {\setminus} T.$![]() The notion of Green index for subsemigroups was introduced in [Reference Gray and Ruškuc10].
The notion of Green index for subsemigroups was introduced in [Reference Gray and Ruškuc10].
Proposition 5.3 Let $S$![]() be a semigroup, and let $T$
be a semigroup, and let $T$![]() be a subsemigroup of $S$
be a subsemigroup of $S$![]() such that $S {\setminus} T$
such that $S {\setminus} T$![]() is a finite union of $\mathcal {R}^{T}$
is a finite union of $\mathcal {R}^{T}$![]() -classes. Then $S$
-classes. Then $S$![]() is weakly right noetherian if and only if $T$
is weakly right noetherian if and only if $T$![]() is weakly right noetherian.
is weakly right noetherian.
Proof. ($\Rightarrow$![]() ) Let $I$
) Let $I$![]() be a right ideal of $T$
be a right ideal of $T$![]() . Let $I^{\prime }=IS^{1};$
. Let $I^{\prime }=IS^{1};$![]() that is, the right ideal of $S$
that is, the right ideal of $S$![]() generated by $I.$
generated by $I.$![]() Since $S$
Since $S$![]() is weakly right noetherian, we have that $I^{\prime }$
is weakly right noetherian, we have that $I^{\prime }$![]() is generated by some finite subset $X\subseteq I$
is generated by some finite subset $X\subseteq I$![]() by Lemma 3.9. Let $R_1,\, \ldots ,\, R_n$
by Lemma 3.9. Let $R_1,\, \ldots ,\, R_n$![]() be the $\mathcal {R}^{T}$
be the $\mathcal {R}^{T}$![]() -classes in $S {\setminus} T,$
-classes in $S {\setminus} T,$![]() and for each $i\in \{1,\, \ldots \, n\}$
and for each $i\in \{1,\, \ldots \, n\}$![]() fix $r_i\in R_i.$
fix $r_i\in R_i.$![]() We claim that $I$
We claim that $I$![]() is generated by the finite set
is generated by the finite set
Indeed, let $a\in I.$![]() Then $a\in I^{\prime },$
Then $a\in I^{\prime },$![]() so $a=xs$
so $a=xs$![]() for some $x\in X$
for some $x\in X$![]() and $s\in S^{1}.$
and $s\in S^{1}.$![]() If $s\in T^{1},$
If $s\in T^{1},$![]() then $a\in YT^{1}.$
then $a\in YT^{1}.$![]() If $s\in S {\setminus} T,$
If $s\in S {\setminus} T,$![]() then $s\in R_i$
then $s\in R_i$![]() for some $i\in \{1,\, \ldots ,\, n\},$
for some $i\in \{1,\, \ldots ,\, n\},$![]() so there exist $t,\, u\in T^{1}$
so there exist $t,\, u\in T^{1}$![]() such that $s=r_it$
such that $s=r_it$![]() and $r_i=su.$
and $r_i=su.$![]() Then $xr_i=(xs)u=au\in I,$
Then $xr_i=(xs)u=au\in I,$![]() and hence $a=xs=(xr_i)t\in YT^{1},$
and hence $a=xs=(xr_i)t\in YT^{1},$![]() as required.
as required.
($\Leftarrow$![]() ) Each $\mathcal {R}^{S}$
) Each $\mathcal {R}^{S}$![]() -class is a union of $\mathcal {R}^{T}$
-class is a union of $\mathcal {R}^{T}$![]() -classes by [Reference Gray and Ruškuc10, Proposition 9], so $S {\setminus} T$
-classes by [Reference Gray and Ruškuc10, Proposition 9], so $S {\setminus} T$![]() is contained in a finite union of $\mathcal {R}^{S}$
is contained in a finite union of $\mathcal {R}^{S}$![]() -classes, and hence $S$
-classes, and hence $S$![]() is weakly right noetherian by Lemma 5.1.
is weakly right noetherian by Lemma 5.1.
Corollary 5.4 Let $S$![]() be a semigroup and let $T$
be a semigroup and let $T$![]() be subsemigroup of $S$
be subsemigroup of $S$![]() with finite Green index. Then $S$
with finite Green index. Then $S$![]() is weakly right noetherian if and only if $T$
is weakly right noetherian if and only if $T$![]() is weakly right noetherian.
is weakly right noetherian.
Corollary 5.5 Let $S$![]() be a semigroup, and let $T$
be a semigroup, and let $T$![]() be a subsemigroup of $S$
be a subsemigroup of $S$![]() such that $S {\setminus} T$
such that $S {\setminus} T$![]() is finite. Then $S$
is finite. Then $S$![]() is weakly right noetherian if and only if $T$
is weakly right noetherian if and only if $T$![]() is weakly right noetherian.
is weakly right noetherian.
In particular, $S$![]() is weakly right noetherian if and only if $S^{1}$
is weakly right noetherian if and only if $S^{1}$![]() is weakly right noetherian if and only if $S^{0}$
is weakly right noetherian if and only if $S^{0}$![]() is weakly right noetherian.
is weakly right noetherian.
Let $S$![]() be a semigroup and $T$
be a semigroup and $T$![]() a subsemigroup of $S.$
a subsemigroup of $S.$![]() It is easy to see that Green's $\mathcal {R}$
It is easy to see that Green's $\mathcal {R}$![]() -preorder on $T$
-preorder on $T$![]() is contained in the restriction of Green's $\mathcal {R}$
is contained in the restriction of Green's $\mathcal {R}$![]() -preorder on $S$
-preorder on $S$![]() to $T$
to $T$![]() ; that is,
; that is,
We say that $T$![]() preserves $\mathcal {R}$
preserves $\mathcal {R}$![]() (in $S$
(in $S$![]() ), or is $\mathcal {R}$
), or is $\mathcal {R}$![]() -preserving, if
-preserving, if
It can be easily shown that if $T$![]() preserves $\mathcal {R},$
preserves $\mathcal {R},$![]() then ${\mathcal {R}_T}$
then ${\mathcal {R}_T}$![]() is the restriction of $\mathcal {R}_S$
is the restriction of $\mathcal {R}_S$![]() to $T.$
to $T.$![]() The next result states that the property of being weakly right noetherian is inherited by $\mathcal {R}$
The next result states that the property of being weakly right noetherian is inherited by $\mathcal {R}$![]() -preserving subsemigroups.
-preserving subsemigroups.
Proposition 5.6 Let $S$![]() be a semigroup and let $T$
be a semigroup and let $T$![]() be an $\mathcal {R}$
be an $\mathcal {R}$![]() -preserving subsemigroup of $S.$
-preserving subsemigroup of $S.$![]() If $S$
If $S$![]() is weakly right noetherian, then so is $T.$
is weakly right noetherian, then so is $T.$![]()
Proof. Let $I$![]() be a right ideal of $T,$
be a right ideal of $T,$![]() and let $I^{\prime }=IS^{1}.$
and let $I^{\prime }=IS^{1}.$![]() Since $S$
Since $S$![]() is weakly right noetherian, $I^{\prime }=XS^{1}$
is weakly right noetherian, $I^{\prime }=XS^{1}$![]() for some finite subset $X\subseteq I.$
for some finite subset $X\subseteq I.$![]() If $a\in I,$
If $a\in I,$![]() then $a\in xS^{1}$
then $a\in xS^{1}$![]() for some $x\in X,$
for some $x\in X,$![]() so $a\leq _{\mathcal {R}_S}\!x.$
so $a\leq _{\mathcal {R}_S}\!x.$![]() By assumption, we have $a\leq _{\mathcal {R}_T}\!x,$
By assumption, we have $a\leq _{\mathcal {R}_T}\!x,$![]() so $a\in xT^{1}.$
so $a\in xT^{1}.$![]() Thus $I=XT^{1}$
Thus $I=XT^{1}$![]() is finitely generated.
is finitely generated.
For a regular subsemigroup $T$![]() of a semigroup $S,$
of a semigroup $S,$![]() Green's relation $\mathcal {R}_T$
Green's relation $\mathcal {R}_T$![]() is the restriction of $\mathcal {R}_S$
is the restriction of $\mathcal {R}_S$![]() to $T$
to $T$![]() (likewise, $\mathcal {L}_T$
(likewise, $\mathcal {L}_T$![]() and $\mathcal {H}_T$
and $\mathcal {H}_T$![]() are the restrictions to $T$
are the restrictions to $T$![]() of $\mathcal {L}_S$
of $\mathcal {L}_S$![]() and $\mathcal {H}_S,$
and $\mathcal {H}_S,$![]() respectively) [Reference Howie13, Proposition 2.4.2]. In fact, $T$
respectively) [Reference Howie13, Proposition 2.4.2]. In fact, $T$![]() preserves $\mathcal {R}.$
preserves $\mathcal {R}.$![]() Indeed, if $a,\, b\in T$
Indeed, if $a,\, b\in T$![]() and $a\leq _{\mathcal {R}_S}b,$
and $a\leq _{\mathcal {R}_S}b,$![]() then there exists $s\in S^{1}$
then there exists $s\in S^{1}$![]() such that $a=bs.$
such that $a=bs.$![]() Letting $b^{\prime }$
Letting $b^{\prime }$![]() be any inverse of $b,$
be any inverse of $b,$![]() we have that $a=bb^{\prime }bs=b(b^{\prime }a)\in bT,$
we have that $a=bb^{\prime }bs=b(b^{\prime }a)\in bT,$![]() so $a\leq _{\mathcal {R}_T}b,$
so $a\leq _{\mathcal {R}_T}b,$![]() as required. Thus, by Proposition 5.6, we have:
as required. Thus, by Proposition 5.6, we have:
Corollary 5.7 Let $S$![]() be a semigroup with a regular subsemigroup $T.$
be a semigroup with a regular subsemigroup $T.$![]() If $S$
If $S$![]() is weakly right noetherian, then so is $T.$
is weakly right noetherian, then so is $T.$![]()
We say that a semigroup $S$![]() has local right identities if $a\in aS$
has local right identities if $a\in aS$![]() for every $a\in S.$
for every $a\in S.$![]() It is easy to show that the class of semigroups with local right identities includes all regular semigroups, right simple semigroups and monoids. The notion of having local right identities will be crucial in § 6.1.
It is easy to show that the class of semigroups with local right identities includes all regular semigroups, right simple semigroups and monoids. The notion of having local right identities will be crucial in § 6.1.
Corollary 5.8 Let $S$![]() be a semigroup, and let $I$
be a semigroup, and let $I$![]() be a right ideal of $S$
be a right ideal of $S$![]() with local right identities. If $S$
with local right identities. If $S$![]() is weakly right noetherian, then so is $I.$
is weakly right noetherian, then so is $I.$![]()
Proof. We prove that $I$![]() preserves $\mathcal {R}$
preserves $\mathcal {R}$![]() in $S.$
in $S.$![]() We just need to show that $\leq _{\mathcal {R}_S}\!\cap~(I\times I) \subseteq \leq _{\mathcal {R}_I.}$
We just need to show that $\leq _{\mathcal {R}_S}\!\cap~(I\times I) \subseteq \leq _{\mathcal {R}_I.}$![]() So, let $(a,\, b)\in I\times I$
So, let $(a,\, b)\in I\times I$![]() and $a\leq _{\mathcal {R}_S}b.$
and $a\leq _{\mathcal {R}_S}b.$![]() Then $a\in bS^{1}.$
Then $a\in bS^{1}.$![]() Since $I$
Since $I$![]() is a right ideal with local right identities, we have
is a right ideal with local right identities, we have
so $a\leq _{\mathcal {R}_I}b,$![]() as required.
as required.
A subsemigroup $T$![]() of a semigroup $S$
of a semigroup $S$![]() is called right unitary (in $S$
is called right unitary (in $S$![]() ) if it satisfies the following condition: for all $a\in T$
) if it satisfies the following condition: for all $a\in T$![]() and $b\in S,$
and $b\in S,$![]() if $ab\in T$
if $ab\in T$![]() then $b\in T.$
then $b\in T.$![]()
Clearly, a right unitary subsemigroup is $\mathcal {R}$![]() -preserving, so we deduce the following corollary, first proven in [Reference Jespers and Okniński14], from Proposition 5.6.
-preserving, so we deduce the following corollary, first proven in [Reference Jespers and Okniński14], from Proposition 5.6.
Corollary 5.9 Jespers and Okniński [Reference Jespers and Okniński14, Lemma 1.1(1)]
Let $S$![]() be a semigroup and let $T$
be a semigroup and let $T$![]() be a right unitary subsemigroup of $S.$
be a right unitary subsemigroup of $S.$![]() If $S$
If $S$![]() is weakly right noetherian, then so is $T.$
is weakly right noetherian, then so is $T.$![]()
If the complement of a subsemigroup is a left ideal, then the subsemigroup is right unitary, so we have:
Corollary 5.10 Let $S$![]() be a semigroup with a subsemigroup $T$
be a semigroup with a subsemigroup $T$![]() such that $S {\setminus} T$
such that $S {\setminus} T$![]() is a left ideal of $S.$
is a left ideal of $S.$![]() If $S$
If $S$![]() is weakly right noetherian, then so is $T.$
is weakly right noetherian, then so is $T.$![]()
Corollary 5.11 Let $S$![]() be a semigroup with a subsemigroup $T$
be a semigroup with a subsemigroup $T$![]() such that $S {\setminus} T$
such that $S {\setminus} T$![]() is a weakly right noetherian ideal of $S.$
is a weakly right noetherian ideal of $S.$![]() Then $S$
Then $S$![]() is weakly right noetherian if and only if $T$
is weakly right noetherian if and only if $T$![]() is weakly right noetherian.
is weakly right noetherian.
Proof. The direct implication follows from Corollary 5.10. For the converse, let $I=S {\setminus} T$![]() . Since $T$
. Since $T$![]() is weakly right noetherian, so is $S/I\cong T\cup \{0\}$
is weakly right noetherian, so is $S/I\cong T\cup \{0\}$![]() by Corollary 5.5. It now follows from Corollary 4.7 that $S$
by Corollary 5.5. It now follows from Corollary 4.7 that $S$![]() is weakly right noetherian.
is weakly right noetherian.
The final part of this section concerns semigroups with a kernel.
Proposition 5.12 Let $S$![]() be a semigroup with a minimal right ideal. If $S$
be a semigroup with a minimal right ideal. If $S$![]() is weakly right noetherian, then the kernel $K=K(S)$
is weakly right noetherian, then the kernel $K=K(S)$![]() is a finite union of pairwise incomparable $\mathcal {R}_K$
is a finite union of pairwise incomparable $\mathcal {R}_K$![]() -classes and is hence weakly right noetherian.
-classes and is hence weakly right noetherian.
Proof. The kernel $K$![]() is the union of all the minimal right ideals of $S$
is the union of all the minimal right ideals of $S$![]() [Reference Clifford3, Theorem 2.1]. Due to their minimality, these minimal right ideals are single $\mathcal {R}_S$
[Reference Clifford3, Theorem 2.1]. Due to their minimality, these minimal right ideals are single $\mathcal {R}_S$![]() -classes and are pairwise incomparable. By Theorem 3.2, there are only finitely many of them. By [Reference Clifford3, Theorem 2.4], each of these minimal right ideals is a single $\mathcal {R}_K$
-classes and are pairwise incomparable. By Theorem 3.2, there are only finitely many of them. By [Reference Clifford3, Theorem 2.4], each of these minimal right ideals is a single $\mathcal {R}_K$![]() -class (so $K$
-class (so $K$![]() is $\mathcal {R}$
is $\mathcal {R}$![]() -preserving). It now follows from Corollary 3.3 that $K$
-preserving). It now follows from Corollary 3.3 that $K$![]() is weakly right noetherian.
is weakly right noetherian.
Let $S$![]() be a semigroup with a zero $0.$
be a semigroup with a zero $0.$![]() The right socle of $S,$
The right socle of $S,$![]() denoted by $\Sigma _r(S),$
denoted by $\Sigma _r(S),$![]() is the union of $\{0\}$
is the union of $\{0\}$![]() and all the $0$
and all the $0$![]() -minimal right ideals of $S.$
-minimal right ideals of $S.$![]() It turns out that $\Sigma _r(S)$
It turns out that $\Sigma _r(S)$![]() is an ideal of $S,$
is an ideal of $S,$![]() as noted in [Reference Clifford and Preston4, Section 6.3]. A similar argument to the one in the proof of Proposition 5.12 yields:
as noted in [Reference Clifford and Preston4, Section 6.3]. A similar argument to the one in the proof of Proposition 5.12 yields:
Proposition 5.13 Let $S$![]() be a semigroup with zero. If $S$
be a semigroup with zero. If $S$![]() is weakly right noetherian, then the right socle $\Sigma _r(S)$
is weakly right noetherian, then the right socle $\Sigma _r(S)$![]() consists of $\{0\}$
consists of $\{0\}$![]() and a finite union of incomparable $\mathcal {R}$
and a finite union of incomparable $\mathcal {R}$![]() -classes, and hence $\Sigma _r(S)$
-classes, and hence $\Sigma _r(S)$![]() is weakly right noetherian.
is weakly right noetherian.
Open Problem 5.14 Let $S$![]() be a weakly right noetherian semigroup with a kernel $K.$
be a weakly right noetherian semigroup with a kernel $K.$![]() Is $K$
Is $K$![]() also weakly right noetherian? If $K=\{0\}$
also weakly right noetherian? If $K=\{0\}$![]() and $S$
and $S$![]() has a $0$
has a $0$![]() -minimal ideal $M,$
-minimal ideal $M,$![]() is $M$
is $M$![]() weakly right noetherian?
weakly right noetherian?
6. Constructions
In this section, we investigate the behaviour of the property of being weakly right noetherian under the following semigroup-theoretic constructions: direct products, free products, semilattices of semigroups, Rees matrix semigroups, Brandt extensions and Bruck–Reilly extensions.
6.1. Direct products
The problem of whether the property of being weakly right noetherian is preserved under direct products was previously considered in [Reference Davvaz and Nazemian6], where it was shown that the direct product of two weakly right noetherian commutative monoids is weakly right noetherian [Reference Davvaz and Nazemian6, Theorem 3.8].
The purpose of this subsection is to provide necessary and sufficient conditions for the direct product of two semigroups to be weakly right notherian.
Recall that a semigroup $S$![]() has local right identities if $a\in aS$
has local right identities if $a\in aS$![]() for every $a\in S.$
for every $a\in S.$![]()
Theorem 6.1 Let $S$![]() and $T$
and $T$![]() be two semigroups with $S$
be two semigroups with $S$![]() infinite.
infinite.
(1) Suppose $T$
 is infinite. Then $S\times T$
is infinite. Then $S\times T$ is weakly right noetherian if and only if both $S$
is weakly right noetherian if and only if both $S$ and $T$
and $T$ are weakly right noetherian and have local right identities.
are weakly right noetherian and have local right identities.(2) Suppose $T$
 is finite. Then $S\times T$
is finite. Then $S\times T$ is weakly right noetherian if and only if $S$
is weakly right noetherian if and only if $S$ is weakly right noetherian and $T$
is weakly right noetherian and $T$ has local right identities.
has local right identities.
In order to prove Theorem 6.1, we first present a couple of preliminary results.
Lemma 6.2 Let $S$![]() and $T$
and $T$![]() be two semigroups with $S$
be two semigroups with $S$![]() infinite. If $S\times T$
infinite. If $S\times T$![]() is weakly right noetherian, then $T$
is weakly right noetherian, then $T$![]() has local right identities.
has local right identities.
Proof. Let $t\in T,$![]() and let $I$
and let $I$![]() be the right ideal of $S\times T$
be the right ideal of $S\times T$![]() generated by the set $\{(s,\, t) : s\in S\}.$
generated by the set $\{(s,\, t) : s\in S\}.$![]() Since $S\times T$
Since $S\times T$![]() is weakly right noetherian, there exists a finite set $X\subseteq S$
is weakly right noetherian, there exists a finite set $X\subseteq S$![]() such that $I$
such that $I$![]() is generated by the set $\{(x,\, t) : x\in X\}.$
is generated by the set $\{(x,\, t) : x\in X\}.$![]()
Choose $s\in S {\setminus} X.$![]() Then $(s,\, t)=(x,\, t)w$
Then $(s,\, t)=(x,\, t)w$![]() for some $x\in X$
for some $x\in X$![]() and $w\in (S\times T)^{1}.$
and $w\in (S\times T)^{1}.$![]() Since $s\neq x,$
Since $s\neq x,$![]() we conclude that $w\in S\times T,$
we conclude that $w\in S\times T,$![]() so $w=(u,\, v)$
so $w=(u,\, v)$![]() for some $u\in S$
for some $u\in S$![]() and $v\in T.$
and $v\in T.$![]() It follows that $t=tv\in tT.$
It follows that $t=tv\in tT.$![]() Since $t$
Since $t$![]() was chosen arbitrarily, $T$
was chosen arbitrarily, $T$![]() has local right identities.
has local right identities.
Proposition 6.3 Let $S$![]() and $T$
and $T$![]() be two semigroups with local right identities. If both $S$
be two semigroups with local right identities. If both $S$![]() and $T$
and $T$![]() are weakly right noetherian, then $S\times T$
are weakly right noetherian, then $S\times T$![]() is weakly right noetherian.
is weakly right noetherian.
Proof. Let $I$![]() be a right ideal of $S\times T.$
be a right ideal of $S\times T.$![]() For each $a\in S,$
For each $a\in S,$![]() define a set
define a set
We claim that $I_a^{T}$![]() is a right ideal of $T.$
is a right ideal of $T.$![]() Indeed, let $t\in I_a^{T}$
Indeed, let $t\in I_a^{T}$![]() and $u\in T.$
and $u\in T.$![]() Since $S$
Since $S$![]() has local right identities, there exists $s\in S$
has local right identities, there exists $s\in S$![]() such that $as=a.$
such that $as=a.$![]() Since $I$
Since $I$![]() is a right ideal of $S\times T,$
is a right ideal of $S\times T,$![]() we have that $(a,\, tu)=(a,\, t)(s,\, u)\in I,$
we have that $(a,\, tu)=(a,\, t)(s,\, u)\in I,$![]() so $tu\in I_a^{T}.$
so $tu\in I_a^{T}.$![]()
Similarly, for each $b\in T$![]() we define a right ideal
we define a right ideal
of $S$![]() . We now make the following claim.
. We now make the following claim.
(1) There exists a finite set $X\subseteq S$
 with the following property: for each $a\in S,$
with the following property: for each $a\in S,$ there exists $x\in X$
there exists $x\in X$ such that $a\in xS$
such that $a\in xS$ and $I_a^{T}=I_x^{T}.$
and $I_a^{T}=I_x^{T}.$
(2) There exists a finite set $Y\subseteq T$
 with the following property: for each $b\in T,$
with the following property: for each $b\in T,$ there exists $y\in Y$
there exists $y\in Y$ such that $b\in yT$
such that $b\in yT$ and $I_b^{S}=I_y^{S}.$
and $I_b^{S}=I_y^{S}.$
Proof of claim. Clearly, it is enough to prove (1). We shall just write $I_a$![]() for $I_a^{T}.$
for $I_a^{T}.$![]() Suppose there are infinitely many right ideals of the form $I_a.$
Suppose there are infinitely many right ideals of the form $I_a.$![]() Note that for any $a,s\in S,$
Note that for any $a,s\in S,$![]() we have $I_a\subseteq I_{as}.$
we have $I_a\subseteq I_{as}.$![]() Write $S=J_1.$
Write $S=J_1.$![]() Since $S$
Since $S$![]() is weakly right noetherian, there exists a finite set $X_1\subseteq J_1$
is weakly right noetherian, there exists a finite set $X_1\subseteq J_1$![]() such that $J_1=X_1S^{1}.$
such that $J_1=X_1S^{1}.$![]() In fact, we have $J_1=X_1S,$
In fact, we have $J_1=X_1S,$![]() since $S$
since $S$![]() having local right identities implies that $X_1\subseteq X_1S.$
having local right identities implies that $X_1\subseteq X_1S.$![]() By our assumption, there exists $x_1\in X_1$
By our assumption, there exists $x_1\in X_1$![]() such that there are infinitely many $a\in x_1S$
such that there are infinitely many $a\in x_1S$![]() with $I_a\neq I_{x_1}.$
with $I_a\neq I_{x_1}.$![]() Consider the set
Consider the set
If $a\in J_2$![]() and $s\in S,$
and $s\in S,$![]() then $I_{x_1}\subsetneq I_a\subseteq I_{as},$
then $I_{x_1}\subsetneq I_a\subseteq I_{as},$![]() so $as\in J_2,$
so $as\in J_2,$![]() and hence $J_2$
and hence $J_2$![]() is a right ideal of $S.$
is a right ideal of $S.$![]() Since $S$
Since $S$![]() is weakly right noetherian, there exists a finite set $X_2\subseteq J_2$
is weakly right noetherian, there exists a finite set $X_2\subseteq J_2$![]() such that $J_2=X_2S,$
such that $J_2=X_2S,$![]() and there exists $x_2\in X_2$
and there exists $x_2\in X_2$![]() such that there are infinitely many $a\in x_2S$
such that there are infinitely many $a\in x_2S$![]() with $I_a\neq I_{x_2}.$
with $I_a\neq I_{x_2}.$![]() Continuing in this way, we obtain an infinite ascending chain
Continuing in this way, we obtain an infinite ascending chain
of right ideals of $T,$![]() but this contradicts the fact that $T$
but this contradicts the fact that $T$![]() is weakly right noetherian. Hence, there exists a finite set $U\subseteq S$
is weakly right noetherian. Hence, there exists a finite set $U\subseteq S$![]() such that $I_a\in \{I_u : u\in U\}$
such that $I_a\in \{I_u : u\in U\}$![]() for every $a\in S.$
for every $a\in S.$![]() For each $u\in U,$
For each $u\in U,$![]() let $K_u$
let $K_u$![]() be the right ideal of $S$
be the right ideal of $S$![]() generated by the set
generated by the set
Since $S$![]() is weakly right noetherian, there exists finite set $X_u\subseteq H_u$
is weakly right noetherian, there exists finite set $X_u\subseteq H_u$![]() such that $H_u=X_uS.$
such that $H_u=X_uS.$![]() Now set $X=\bigcup _{u\in U}X_u$
Now set $X=\bigcup _{u\in U}X_u$![]() . It is clear that $X$
. It is clear that $X$![]() satisfies the condition in the statement of the claim.
satisfies the condition in the statement of the claim.
Returning to the proof of Proposition 6.3, we claim that $I$![]() is generated by the finite set $Z=I\cap (X\times Y).$
is generated by the finite set $Z=I\cap (X\times Y).$![]() Indeed, let $(a,\, b)\in I.$
Indeed, let $(a,\, b)\in I.$![]() Then $a\in I_b^{S}$
Then $a\in I_b^{S}$![]() and $b\in I_a^{T}.$
and $b\in I_a^{T}.$![]() By the above claim, there exist $x\in X$
By the above claim, there exist $x\in X$![]() and $s\in S$
and $s\in S$![]() such that $a=xs$
such that $a=xs$![]() and $I_a^{T}=I_x^{T},$
and $I_a^{T}=I_x^{T},$![]() and there exist $y\in Y$
and there exist $y\in Y$![]() and $t\in T$
and $t\in T$![]() such that $b=yt$
such that $b=yt$![]() and $I_b^{S}=I_y^{S}.$
and $I_b^{S}=I_y^{S}.$![]() We have that
We have that
We conclude that
as required.
We are now ready to prove Theorem 6.1.
Proof of Theorem 6.1. Is $S\times T$![]() is weakly right noetherian, then both $S$
is weakly right noetherian, then both $S$![]() and $T,$
and $T,$![]() being homomorphic images of $S\times T,$
being homomorphic images of $S\times T,$![]() are weakly right noetherian by Lemma 4.1, and $T$
are weakly right noetherian by Lemma 4.1, and $T$![]() has local right identities by Lemma 6.2. If $T$
has local right identities by Lemma 6.2. If $T$![]() is infinite, then $S$
is infinite, then $S$![]() also has local right identities by Lemma 6.2.
also has local right identities by Lemma 6.2.
For the case that $T$![]() is infinite, the converse follows immediately from Proposition 6.3. Now assume that $T$
is infinite, the converse follows immediately from Proposition 6.3. Now assume that $T$![]() is finite, and suppose that $S$
is finite, and suppose that $S$![]() is weakly right noetherian and $T$
is weakly right noetherian and $T$![]() has local right identities. We have that $S^{1}$
has local right identities. We have that $S^{1}$![]() is weakly right noetherian by Corollary 5.5, and clearly $S^{1}$
is weakly right noetherian by Corollary 5.5, and clearly $S^{1}$![]() has local right identities. Therefore, by Proposition 6.3, we have that $S^{1}\times T$
has local right identities. Therefore, by Proposition 6.3, we have that $S^{1}\times T$![]() is weakly right noetherian. Since $(S^{1}\times T) {\setminus} (S\times T)$
is weakly right noetherian. Since $(S^{1}\times T) {\setminus} (S\times T)$![]() is finite, it follows from Corollary 5.5 that $S\times T$
is finite, it follows from Corollary 5.5 that $S\times T$![]() is weakly right noetherian.
is weakly right noetherian.
6.2. Free products
We shall define the free product of two semigroups (respectively monoids) in terms of semigroup (respectively monoid) presentations. For more information about semigroup and monoid presentations, we refer the reader to [Reference Clifford3, Section 9.1].
Given two semigroups $S$![]() and $T$
and $T$![]() defined by presentations $\langle X\,|\,Q\rangle$
defined by presentations $\langle X\,|\,Q\rangle$![]() and $\langle Y\,|\,R\rangle ,$
and $\langle Y\,|\,R\rangle ,$![]() respectively, the semigroup free product of $S$
respectively, the semigroup free product of $S$![]() and $T,$
and $T,$![]() denoted by $S\ast T,$
denoted by $S\ast T,$![]() is the semigroup defined by the presentation $\langle X,\, Y\,|\,Q,\, R\rangle .$
is the semigroup defined by the presentation $\langle X,\, Y\,|\,Q,\, R\rangle .$![]() If $S$
If $S$![]() and $T$
and $T$![]() are monoids, then the monoid free product of $S$
are monoids, then the monoid free product of $S$![]() and $T,$
and $T,$![]() denoted by $S\ast _1\,T,$
denoted by $S\ast _1\,T,$![]() is the monoid defined by the presentation $\langle X,\, Y\,|\,Q,\, R,\, 1_S=1_T\rangle ,$
is the monoid defined by the presentation $\langle X,\, Y\,|\,Q,\, R,\, 1_S=1_T\rangle ,$![]() where $1_S$
where $1_S$![]() is a fixed word over $X$
is a fixed word over $X$![]() representing the identity of $S$
representing the identity of $S$![]() and $1_T$
and $1_T$![]() is a fixed word over $Y$
is a fixed word over $Y$![]() representing the identity of $T.$
representing the identity of $T.$![]() In the case that $S$
In the case that $S$![]() and $T$
and $T$![]() are groups, the monoid free product $S\ast _1\,T$
are groups, the monoid free product $S\ast _1\,T$![]() coincides with the group free product of $S$
coincides with the group free product of $S$![]() and $T$
and $T$![]() ; this fact is noted in [Reference Howie13, Section 8.2, p. 266].
; this fact is noted in [Reference Howie13, Section 8.2, p. 266].
In the following, we provide necessary and sufficient conditions for the semigroup (respectively monoid) free product of two semigroups (respectively monoids) to be weakly right noetherian.
Theorem 6.4 Let $S$![]() and $T$
and $T$![]() be two semigroups. Then $S\ast T$
be two semigroups. Then $S\ast T$![]() is weakly right noetherian if and only if both $S$
is weakly right noetherian if and only if both $S$![]() and $T$
and $T$![]() are trivial.
are trivial.
Proof. We denote $S\ast T$![]() by $U.$
by $U.$![]()
$(\Rightarrow ).$![]() Suppose that $T$
Suppose that $T$![]() is non-trivial, and choose $a\in S$
is non-trivial, and choose $a\in S$![]() and distinct elements $b,\, c\in T.$
and distinct elements $b,\, c\in T.$![]() For $i\in \mathbb {N},$
For $i\in \mathbb {N},$![]() let $u_i=(ab)^{i}aca.$
let $u_i=(ab)^{i}aca.$![]() Let $I$
Let $I$![]() be the right ideal of $U$
be the right ideal of $U$![]() generated by the set $X=\{u_i : i\in \mathbb {N}\}.$
generated by the set $X=\{u_i : i\in \mathbb {N}\}.$![]() For any $i\in \mathbb {N},$
For any $i\in \mathbb {N},$![]() the element $u_i$
the element $u_i$![]() cannot we written as $u_jv$
cannot we written as $u_jv$![]() for any $j\neq i$
for any $j\neq i$![]() and $v\in U,$
and $v\in U,$![]() so $X$
so $X$![]() is a minimal generating set for $I$
is a minimal generating set for $I$![]() and hence $I$
and hence $I$![]() is not finitely generated. Therefore, $U$
is not finitely generated. Therefore, $U$![]() is not weakly right noetherian.
is not weakly right noetherian.
$(\Leftarrow ).$![]() The semigroup $U$
The semigroup $U$![]() is defined by the presentation
is defined by the presentation
Then $U$![]() is the disjoint union of the following subsemigroups:
is the disjoint union of the following subsemigroups:
Since $\mathbb {N}$![]() and $\mathbb {N}_0$
and $\mathbb {N}_0$![]() are weakly right noetherian, it follows from Lemma 3.11 that $U$
are weakly right noetherian, it follows from Lemma 3.11 that $U$![]() is weakly right noetherian.
is weakly right noetherian.
Before stating our next result, we first make some definitions.
Let $M$![]() and $N$
and $N$![]() be two disjoint monoids. A reduced sequence over $M$
be two disjoint monoids. A reduced sequence over $M$![]() and $N$
and $N$![]() is a sequence $(u_1,\, \ldots ,\, u_n)$
is a sequence $(u_1,\, \ldots ,\, u_n)$![]() such that: $u_i\in (M\cup N) {\setminus} \{1_M,\, 1_N\}$
such that: $u_i\in (M\cup N) {\setminus} \{1_M,\, 1_N\}$![]() for each $i\in \{1,\, \ldots ,\, n\}$
for each $i\in \{1,\, \ldots ,\, n\}$![]() ; $(u_i,\, u_{i+1})\in M\times N$
; $(u_i,\, u_{i+1})\in M\times N$![]() or $(u_i,\, u_{i+1})\in N\times M$
or $(u_i,\, u_{i+1})\in N\times M$![]() for each $i\in \{1,\, \ldots ,\, n-1\}.$
for each $i\in \{1,\, \ldots ,\, n-1\}.$![]()
Every non-identity element of $M\ast _{1}N$![]() can be uniquely written as $u_1\cdots u_n$
can be uniquely written as $u_1\cdots u_n$![]() for some reduced sequence $(u_1,\, \ldots ,\, u_n)$
for some reduced sequence $(u_1,\, \ldots ,\, u_n)$![]() over $M$
over $M$![]() and $N$
and $N$![]() [Reference Clifford and Preston4, Section 9.4]; the elements $u_i,\, 1\leq i\leq n,$
[Reference Clifford and Preston4, Section 9.4]; the elements $u_i,\, 1\leq i\leq n,$![]() are called the free factors of $u_1\cdots u_n.$
are called the free factors of $u_1\cdots u_n.$![]()
Theorem 6.5 Let $M$![]() and $N$
and $N$![]() be two monoids. Then $M\ast _1N$
be two monoids. Then $M\ast _1N$![]() is weakly right noetherian if and only if one of the following holds:
is weakly right noetherian if and only if one of the following holds:
(1) $M$
 is weakly right noetherian and $N$
is weakly right noetherian and $N$ is trivial, or vice versa$;$
is trivial, or vice versa$;$
(2) both $M$
 and $N$
and $N$ contain precisely two elements$;$
contain precisely two elements$;$
(3) both $M$
 and $N$
and $N$ are groups.
are groups.
Proof. We denote $M\ast _1N$![]() by $U.$
by $U.$![]() If $N$
If $N$![]() is trivial, then $M$
is trivial, then $M$![]() is isomorphic to $U,$
is isomorphic to $U,$![]() so we may assume that both $M$
so we may assume that both $M$![]() and $N$
and $N$![]() are non-trivial.
are non-trivial.
$(\Rightarrow ).$![]() Suppose for a contradiction that $|N|\geq 3$
Suppose for a contradiction that $|N|\geq 3$![]() and at least one of $M$
and at least one of $M$![]() and $N$
and $N$![]() is not a group. A monoid in which every element is right invertible is a group. Therefore, we can choose $a\in M {\setminus} \{1\}$
is not a group. A monoid in which every element is right invertible is a group. Therefore, we can choose $a\in M {\setminus} \{1\}$![]() and distinct elements $b,\, c\in N {\setminus} \{1\}$
and distinct elements $b,\, c\in N {\setminus} \{1\}$![]() such that at least one of $a,\, b,\, c$
such that at least one of $a,\, b,\, c$![]() is not right invertible. Let $u_i=(ab)^{i}acab$
is not right invertible. Let $u_i=(ab)^{i}acab$![]() for $i\in \mathbb {N},$
for $i\in \mathbb {N},$![]() and let $I$
and let $I$![]() be the right ideal of $U$
be the right ideal of $U$![]() generated by $\{u_i : i\in \mathbb {N}\}$
generated by $\{u_i : i\in \mathbb {N}\}$![]() . Suppose that $I$
. Suppose that $I$![]() is finitely generated. Then it can be generated by a finite set
is finitely generated. Then it can be generated by a finite set
Then $u_{k+1}=u_iv$![]() for some $i\in \{1,\, \ldots ,\, k\}$
for some $i\in \{1,\, \ldots ,\, k\}$![]() and $v\in U.$
and $v\in U.$![]() Since at least one of $a,\, b,\, c$
Since at least one of $a,\, b,\, c$![]() is not right invertible, the first $2i+2$
is not right invertible, the first $2i+2$![]() free factors of $u_iv$
free factors of $u_iv$![]() are $a,\, b,\, \ldots ,\, a,\, b,\, a,\, c.$
are $a,\, b,\, \ldots ,\, a,\, b,\, a,\, c.$![]() But the free factor in position $2i+2$
But the free factor in position $2i+2$![]() of $u_{k+1}$
of $u_{k+1}$![]() is $b,$
is $b,$![]() so we have a contradiction. Hence, $I$
so we have a contradiction. Hence, $I$![]() is not finitely generated and $U$
is not finitely generated and $U$![]() is not weakly right noetherian.
is not weakly right noetherian.
$(\Leftarrow ).$![]() If $M$
If $M$![]() and $N$
and $N$![]() are both groups, then $U$
are both groups, then $U$![]() is also a group and hence weakly right noetherian.
is also a group and hence weakly right noetherian.
Now suppose that both $M$![]() and $N$
and $N$![]() contain precisely two elements and that $N$
contain precisely two elements and that $N$![]() is not a group. Then $N$
is not a group. Then $N$![]() is isomorphic to the two-element semilattice $\{1,\, 0\},$
is isomorphic to the two-element semilattice $\{1,\, 0\},$![]() and $M$
and $M$![]() is isomorphic to either $\{1,\, 0\}$
is isomorphic to either $\{1,\, 0\}$![]() or $\mathbb {Z}_2.$
or $\mathbb {Z}_2.$![]()
If $M\cong \{1,\, 0\},$![]() then $U$
then $U$![]() is isomorphic to $V^{1}$
is isomorphic to $V^{1}$![]() where $V$
where $V$![]() is the free product of two trivial semigroups. It follows from Theorem 6.4 and Corollary 5.5 that $U$
is the free product of two trivial semigroups. It follows from Theorem 6.4 and Corollary 5.5 that $U$![]() is weakly right noetherian.
is weakly right noetherian.
If $M\cong \mathbb {Z}_2,$![]() then $U$
then $U$![]() is defined by the monoid presentation
is defined by the monoid presentation
Let $u_1=ab,\, u_2=ba$![]() and $u_3=bab,$
and $u_3=bab,$![]() and let $U_i=\{u_i^{n} : n\geq 0\}$
and let $U_i=\{u_i^{n} : n\geq 0\}$![]() for $i=1,\, 2,\, 3.$
for $i=1,\, 2,\, 3.$![]() Also, let $U_4=\{u_1^{n}(aba) : n\geq 0\}.$
Also, let $U_4=\{u_1^{n}(aba) : n\geq 0\}.$![]() Then each $U_i$
Then each $U_i$![]() is isomorphic to the free monogenic monoid $\mathbb {N}_0$
is isomorphic to the free monogenic monoid $\mathbb {N}_0$![]() , and $U=\bigcup _{i=1}^{4}U_i.$
, and $U=\bigcup _{i=1}^{4}U_i.$![]() Since $\mathbb {N}_0$
Since $\mathbb {N}_0$![]() is weakly right noetherian, it follows from Lemma 3.11 that $U$
is weakly right noetherian, it follows from Lemma 3.11 that $U$![]() is weakly right noetherian.
is weakly right noetherian.
6.3. Semilattices of semigroups
Let $Y$![]() be a semilattice and let $(S_{\alpha })_{\alpha \in Y}$
be a semilattice and let $(S_{\alpha })_{\alpha \in Y}$![]() be a family of disjoint semigroups, indexed by $Y.$
be a family of disjoint semigroups, indexed by $Y.$![]() If $S=\bigcup _{\alpha \in Y}S_{\alpha }$
If $S=\bigcup _{\alpha \in Y}S_{\alpha }$![]() is a semigroup such that $S_{\alpha }S_{\beta }\subseteq S_{\alpha \beta }$
is a semigroup such that $S_{\alpha }S_{\beta }\subseteq S_{\alpha \beta }$![]() for all $\alpha ,\, \beta \in Y,$
for all $\alpha ,\, \beta \in Y,$![]() then $S$
then $S$![]() is called a semilattice of semigroups, and we denote it by $S=\mathcal {S}(Y,\, S_{\alpha }).$
is called a semilattice of semigroups, and we denote it by $S=\mathcal {S}(Y,\, S_{\alpha }).$![]()
Now let $S=\bigcup _{\alpha \in Y}S_{\alpha },$![]() and suppose that for each $\alpha ,\, \beta \in Y$
and suppose that for each $\alpha ,\, \beta \in Y$![]() with $\alpha \geq \beta$
with $\alpha \geq \beta$![]() there exists a homomorphism $\phi _{\alpha , \beta } : S_{\alpha }\to S_{\beta }.$
there exists a homomorphism $\phi _{\alpha , \beta } : S_{\alpha }\to S_{\beta }.$![]() Furthermore, assume that:
Furthermore, assume that:
• for each $\alpha \in Y,$
 the homomorphism $\phi _{\alpha , \alpha }$
the homomorphism $\phi _{\alpha , \alpha }$ is the identity map on $S_{\alpha }$
is the identity map on $S_{\alpha }$ ;
;• for each $\alpha ,\, \beta ,\, \gamma \in Y$
 with $\alpha \geq \beta \geq \gamma$
with $\alpha \geq \beta \geq \gamma$ , we have $\phi _{\alpha , \beta }\phi _{\beta , \gamma }=\phi _{\alpha , \gamma }.$
, we have $\phi _{\alpha , \beta }\phi _{\beta , \gamma }=\phi _{\alpha , \gamma }.$
For $a\in S_{\alpha }$![]() and $b\in S_{\beta },$
and $b\in S_{\beta },$![]() we define
we define
With this multiplication, $S$![]() is a semilattice of semigroups. In this case, we call $S$
is a semilattice of semigroups. In this case, we call $S$![]() a strong semilattice of semigroups and denote it by $S=\mathcal {S}(Y,\, S_{\alpha },\, \phi _{\alpha , \beta }).$
a strong semilattice of semigroups and denote it by $S=\mathcal {S}(Y,\, S_{\alpha },\, \phi _{\alpha , \beta }).$![]()
In the remainder of this section, we investigate under what conditions a (strong) semilattice of semigroups is weakly right noetherian.
The following characterization of weakly right noetherian semilattices follows immediately from Theorem 3.2.
Proposition 6.6 Gould et al. [Reference Gould, Hartmann and Shaheen9, Proposition 3.1]
Let $Y$![]() be a (meet-)semilattice. Then $Y$
be a (meet-)semilattice. Then $Y$![]() is weakly noetherian if and only if it contains no infinite strictly ascending chain or infinite antichain of elements.
is weakly noetherian if and only if it contains no infinite strictly ascending chain or infinite antichain of elements.
Since the semilattice $Y$![]() is a homomorphic image of $S=\mathcal {S}(Y,\, S_{\alpha }),$
is a homomorphic image of $S=\mathcal {S}(Y,\, S_{\alpha }),$![]() by Lemma 4.1 we have:
by Lemma 4.1 we have:
Lemma 6.7 Let $S=\mathcal {S}(Y,\, S_{\alpha })$![]() be a semilattice of semigroups. If $S$
be a semilattice of semigroups. If $S$![]() is weakly right noetherian, then $Y$
is weakly right noetherian, then $Y$![]() is weakly noetherian.
is weakly noetherian.
For a semilattice of semigroups $\mathcal {S}(Y,\, S_{\alpha })$![]() to be weakly right noetherian, it is not required that all the $S_{\alpha }$
to be weakly right noetherian, it is not required that all the $S_{\alpha }$![]() be weakly right noetherian. In order to show this, we consider the following construction, which will be used again later in the paper.
be weakly right noetherian. In order to show this, we consider the following construction, which will be used again later in the paper.
Construction 6.8 Let $S$![]() and $T$
and $T$![]() be two semigroups with homomorphisms $\theta ,\, \phi : S\to T.$
be two semigroups with homomorphisms $\theta ,\, \phi : S\to T.$![]() Let $N_T=\{x_t : t\in T\}\cup \{0\}$
Let $N_T=\{x_t : t\in T\}\cup \{0\}$![]() be a null semigroup disjoint from $S.$
be a null semigroup disjoint from $S.$![]() We define a multiplication on $S\cup N_T,$
We define a multiplication on $S\cup N_T,$![]() extending those on $S$
extending those on $S$![]() and $N_T,$
and $N_T,$![]() as follows:
as follows:
With this multiplication, $S\cup N_T$![]() is a semigroup. We denote it by $\mathcal {U}(S,\, T; \theta ,\, \phi ).$
is a semigroup. We denote it by $\mathcal {U}(S,\, T; \theta ,\, \phi ).$![]() We simplify this expression in the case that $S=T$
We simplify this expression in the case that $S=T$![]() by only writing $S$
by only writing $S$![]() once, and similarly if $\theta =\phi .$
once, and similarly if $\theta =\phi .$![]()
We may view $\mathcal {U}(S,\, T; \theta ,\, \phi )$![]() as a semilattice of semigroups, where the structure semilattice is $\{\alpha ,\, 0\}$
as a semilattice of semigroups, where the structure semilattice is $\{\alpha ,\, 0\}$![]() and the corresponding subsemigroups are $S$
and the corresponding subsemigroups are $S$![]() and $N_T,$
and $N_T,$![]() respectively. Every non-zero element of a null semigroup is indecomposable, so infinite null semigroups are not weakly right noetherian by Lemma 3.10. Therefore, the following result yields the desired counterexample.
respectively. Every non-zero element of a null semigroup is indecomposable, so infinite null semigroups are not weakly right noetherian by Lemma 3.10. Therefore, the following result yields the desired counterexample.
Proposition 6.9 Let $S$![]() and $T$
and $T$![]() be two semigroups with homomorphisms $\theta ,\, \phi : S\to T$
be two semigroups with homomorphisms $\theta ,\, \phi : S\to T$![]() where $\phi$
where $\phi$![]() is surjective, and let $U=\mathcal {U}(S,\, T; \theta ,\, \phi ).$
is surjective, and let $U=\mathcal {U}(S,\, T; \theta ,\, \phi ).$![]() Then $U$
Then $U$![]() is weakly right noetherian if and only if $S$
is weakly right noetherian if and only if $S$![]() is weakly right noetherian.
is weakly right noetherian.
Proof. If $U$![]() is weakly right noetherian, then since $U {\setminus} S=N_T$
is weakly right noetherian, then since $U {\setminus} S=N_T$![]() is an ideal of $U,$
is an ideal of $U,$![]() we have that $S$
we have that $S$![]() is weakly right noetherian by Corollary 5.10.
is weakly right noetherian by Corollary 5.10.
Conversely, suppose $S$![]() is weakly right noetherian, and let $I$
is weakly right noetherian, and let $I$![]() be a right ideal of $U.$
be a right ideal of $U.$![]() Now $I\cap S$
Now $I\cap S$![]() is either empty or a right ideal of $S$
is either empty or a right ideal of $S$![]() ; in the latter case it is generated by a finite set $Y$
; in the latter case it is generated by a finite set $Y$![]() since $S$
since $S$![]() is weakly right noetherian. We have that $T$
is weakly right noetherian. We have that $T$![]() is weakly right noetherian by Lemma 4.1. In particular, $T=AT^{1}$
is weakly right noetherian by Lemma 4.1. In particular, $T=AT^{1}$![]() for some finite set $A\subseteq T.$
for some finite set $A\subseteq T.$![]() For each $a\in A,$
For each $a\in A,$![]() define a set
define a set
Let $A^{\prime }$![]() be the set of elements in $A$
be the set of elements in $A$![]() such that $I_a\neq \emptyset .$
such that $I_a\neq \emptyset .$![]() For each $a\in A^{\prime },$
For each $a\in A^{\prime },$![]() we have that $I_a$
we have that $I_a$![]() is a right ideal of $S,$
is a right ideal of $S,$![]() so it is generated by some finite set $U_a$
so it is generated by some finite set $U_a$![]() since $S$
since $S$![]() is weakly right noetherian. We claim that $I$
is weakly right noetherian. We claim that $I$![]() is generated by the finite set
is generated by the finite set

Let $u\in I.$![]() If $u\in S,$
If $u\in S,$![]() then $u\in I\cap S=YS^{1}.$
then $u\in I\cap S=YS^{1}.$![]() Clearly, $0\in ZU,$
Clearly, $0\in ZU,$![]() so we just need to consider the case that $u=x_t$
so we just need to consider the case that $u=x_t$![]() for some $t\in T.$
for some $t\in T.$![]() Then $t=av$
Then $t=av$![]() for some $a\in A$
for some $a\in A$![]() and $v\in T^{1}.$
and $v\in T^{1}.$![]() If $v=1,$
If $v=1,$![]() then $u=x_a\in Z.$
then $u=x_a\in Z.$![]() Otherwise, let $s\in S$
Otherwise, let $s\in S$![]() be such that $s\theta =v,$
be such that $s\theta =v,$![]() so $s\in I_a=U_aS^{1}.$
so $s\in I_a=U_aS^{1}.$![]() It follows that $u=x_as\in (x_aU_a)S^{1},$
It follows that $u=x_as\in (x_aU_a)S^{1},$![]() as required.
as required.
Remark 6.10 In general, principal factors of weakly right noetherian semigroups need not be weakly right noetherian. Indeed, let $G$![]() be an infinite group. Then $U=\mathcal {U}(G,\, \text {id})$
be an infinite group. Then $U=\mathcal {U}(G,\, \text {id})$![]() is weakly right noetherian. It has three $\mathcal {H}=\mathcal {J}$
is weakly right noetherian. It has three $\mathcal {H}=\mathcal {J}$![]() -classes: $G,$
-classes: $G,$![]() $J=\{x_g : g\in G\}$
$J=\{x_g : g\in G\}$![]() and $\{0\}.$
and $\{0\}.$![]() The principal factor of $J$
The principal factor of $J$![]() is isomorphic to $N_G,$
is isomorphic to $N_G,$![]() which is not weakly right noetherian.
which is not weakly right noetherian.
In the case that a semigroup $S_{\beta },\, \beta \in Y,$![]() has local right identities, it is a necessary condition for $S=\mathcal {S}(Y,\, S_{\alpha })$
has local right identities, it is a necessary condition for $S=\mathcal {S}(Y,\, S_{\alpha })$![]() to be weakly right noetherian that $S_{\beta }$
to be weakly right noetherian that $S_{\beta }$![]() be weakly right noetherian.
be weakly right noetherian.
Lemma 6.11 Let $S=\mathcal {S}(Y,\, S_{\alpha })$![]() be a semilattice of semigroups, let $\beta \in Y,$
be a semilattice of semigroups, let $\beta \in Y,$![]() and suppose that $S_{\beta }$
and suppose that $S_{\beta }$![]() has local right identities. If $S$
has local right identities. If $S$![]() is weakly right noetherian, then so is $S_{\beta }.$
is weakly right noetherian, then so is $S_{\beta }.$![]()
Proof. Let $Y^{\prime }=\{\alpha \in Y : \alpha \ngeq \beta \},$![]() and let $I=\bigcup _{\alpha \in Y^{\prime }}S_{\alpha }.$
and let $I=\bigcup _{\alpha \in Y^{\prime }}S_{\alpha }.$![]() Now, $I$
Now, $I$![]() is an ideal and $T=S {\setminus} I$
is an ideal and $T=S {\setminus} I$![]() is a subsemigroup of $S,$
is a subsemigroup of $S,$![]() so $T$
so $T$![]() is weakly right noetherian by Corollary 5.10. Since $S_{\beta }$
is weakly right noetherian by Corollary 5.10. Since $S_{\beta }$![]() is an ideal of $T$
is an ideal of $T$![]() with local right identities, it is weakly right noetherian by Corollary 5.8.
with local right identities, it is weakly right noetherian by Corollary 5.8.
The following corollary follows from Lemmas 6.11 and 3.11.
Corollary 6.12 Let $S=\mathcal {S}(Y,\, S_{\alpha })$![]() be a semilattice of semigroups where $Y$
be a semilattice of semigroups where $Y$![]() is finite and each $S_{\alpha }$
is finite and each $S_{\alpha }$![]() has local right identities. Then $S$
has local right identities. Then $S$![]() is weakly right noetherian if and only if each $S_{\alpha }$
is weakly right noetherian if and only if each $S_{\alpha }$![]() is weakly right noetherian.
is weakly right noetherian.
We now consider the situation for strong semilattices of semigroups.
Proposition 6.13 Let $S=\mathcal {S}(Y,\, S_{\alpha },\, \phi _{\alpha , \beta })$![]() be a strong semilattice of semigroups. If $S$
be a strong semilattice of semigroups. If $S$![]() is weakly right noetherian, then $Y$
is weakly right noetherian, then $Y$![]() is weakly noetherian and each $S_{\alpha }$
is weakly noetherian and each $S_{\alpha }$![]() is weakly right noetherian.
is weakly right noetherian.
Proof. The semilattice $Y$![]() is weakly noetherian by Lemma 6.7. Now let $\alpha \in Y.$
is weakly noetherian by Lemma 6.7. Now let $\alpha \in Y.$![]() We prove that $S_{\alpha }$
We prove that $S_{\alpha }$![]() preserves $\mathcal {R}$
preserves $\mathcal {R}$![]() in $S,$
in $S,$![]() and hence $S_{\alpha }$
and hence $S_{\alpha }$![]() is weakly right noetherian by Proposition 5.6. We write $\mathcal {R}=\mathcal {R}_S$
is weakly right noetherian by Proposition 5.6. We write $\mathcal {R}=\mathcal {R}_S$![]() and $\mathcal {R}_{\alpha }=\mathcal {R}_{S_{\alpha }}.$
and $\mathcal {R}_{\alpha }=\mathcal {R}_{S_{\alpha }}.$![]() We just need to show that $\leq _{\mathcal {R}}\cap~(S_{\alpha }\times S_{\alpha })\subseteq\leq _{\mathcal {R}_{\alpha }}$
We just need to show that $\leq _{\mathcal {R}}\cap~(S_{\alpha }\times S_{\alpha })\subseteq\leq _{\mathcal {R}_{\alpha }}$![]() . So, let $a,\, b\in S_{\alpha }$
. So, let $a,\, b\in S_{\alpha }$![]() and $a\leq _{\mathcal {R}}b.$
and $a\leq _{\mathcal {R}}b.$![]() Then $a=bs$
Then $a=bs$![]() for some $s\in S^{1}.$
for some $s\in S^{1}.$![]() If $s=1$
If $s=1$![]() then $a=b,$
then $a=b,$![]() so assume that $s\in S.$
so assume that $s\in S.$![]() Then $s\in S_{\beta }$
Then $s\in S_{\beta }$![]() for some $\beta \in Y.$
for some $\beta \in Y.$![]() Since $a=bs\in S_{\alpha }S_{\beta }\subseteq S_{\alpha \beta },$
Since $a=bs\in S_{\alpha }S_{\beta }\subseteq S_{\alpha \beta },$![]() we conclude that $\alpha \beta =\alpha .$
we conclude that $\alpha \beta =\alpha .$![]() It follows that
It follows that
so $a\leq _{\mathcal {R}_{\alpha }}b,$![]() as required.
as required.
Proposition 6.13 and Lemma 3.11 together yield:
Corollary 6.14 Let $S=\mathcal {S}(Y,\, S_{\alpha },\, \phi _{\alpha , \beta })$![]() be a strong semilattice of semigroups where $Y$
be a strong semilattice of semigroups where $Y$![]() is finite. Then $S$
is finite. Then $S$![]() is weakly right noetherian if and only if each $S_{\alpha }$
is weakly right noetherian if and only if each $S_{\alpha }$![]() is weakly right noetherian.
is weakly right noetherian.
Example 7.17 below shows that the converse of Proposition 6.13 does not hold, even in the case that each $S_{\alpha }$![]() is finite.
is finite.
Open Problem 6.15 Find necessary and sufficient conditions for a strong semilattice of semigroups to be weakly right noetherian.
6.4. Rees matrix semigroups and Brandt extensions
Let $S$![]() be a semigroup, let $I$
be a semigroup, let $I$![]() and $J$
and $J$![]() be two non-empty index sets, and let $P=(p_{ji})$
be two non-empty index sets, and let $P=(p_{ji})$![]() be a $J\times I$
be a $J\times I$![]() matrix with entries from $S.$
matrix with entries from $S.$![]() The set $I\times S\times J$
The set $I\times S\times J$![]() becomes a semigroup under the multiplication given by
becomes a semigroup under the multiplication given by
and is called the Rees matrix semigroup over $S$![]() with respect to $P$
with respect to $P$![]() . We denote this semigroup by $\mathcal {M}(S; I,\, J; P)$
. We denote this semigroup by $\mathcal {M}(S; I,\, J; P)$![]() .
.
We now modify the Rees matrix construction as follows. Let the matrix $P$![]() have entries from $S^{0}.$
have entries from $S^{0}.$![]() The set $(I\times S\times J)\cup \{0\}$
The set $(I\times S\times J)\cup \{0\}$![]() with multiplication given by
with multiplication given by

and $0(i,\, s,\, j)=(i,\, s,\, j)0=0^{2}=0,$![]() is a semigroup. It is called the Rees matrix semigroup with zero over $S$
is a semigroup. It is called the Rees matrix semigroup with zero over $S$![]() with respect to $P$
with respect to $P$![]() , and is denoted by $\mathcal {M}^{0}(G; I,\, J; P)$
, and is denoted by $\mathcal {M}^{0}(G; I,\, J; P)$![]() .
.
A semigroup is said to be completely simple if it is simple and contains minimal left and right ideals. A semigroup with zero is said to be completely $0$![]() -simple if it is $0$
-simple if it is $0$![]() -simple and contains $0$
-simple and contains $0$![]() -minimal left and right ideals. Rees [Reference Rees25] proved that a semigroup is completely $0$
-minimal left and right ideals. Rees [Reference Rees25] proved that a semigroup is completely $0$![]() -simple if and only if it is isomorphic to a Rees matrix semigroup with zero $\mathcal {M}^{0}(G; I,\, J; P)$
-simple if and only if it is isomorphic to a Rees matrix semigroup with zero $\mathcal {M}^{0}(G; I,\, J; P)$![]() over a group $G$
over a group $G$![]() such that every row and column of $P$
such that every row and column of $P$![]() contains at least one element in $G.$
contains at least one element in $G.$![]() Consequently, a semigroup is completely simple if and only if it is isomorphic to a Rees matrix semigroup $\mathcal {M}(G; I,\, J; P)$
Consequently, a semigroup is completely simple if and only if it is isomorphic to a Rees matrix semigroup $\mathcal {M}(G; I,\, J; P)$![]() over a group $G.$
over a group $G.$![]()
We shall consider conditions under which a Rees matrix semigroup with zero $T=\mathcal {M}^{0}(S; I,\, J; P)$![]() is weakly right noetherian. We begin by considering what affect $T$
is weakly right noetherian. We begin by considering what affect $T$![]() being weakly right noetherian has on $S$
being weakly right noetherian has on $S$![]() and the index sets $I$
and the index sets $I$![]() and $J.$
and $J.$![]()
Lemma 6.16 Let $T=\mathcal {M}^{0}(S; I,\, J; P)$![]() be weakly right noetherian.
be weakly right noetherian.
(1) The semigroup $S$
 is weakly right noetherian and $I$
is weakly right noetherian and $I$ is finite.
is finite.(2) Let $U$
 be the ideal of $S^{0}$
be the ideal of $S^{0}$ generated by the entries of $P.$
generated by the entries of $P.$ If the set $S {\setminus} U$
If the set $S {\setminus} U$ is non-empty, then both $S {\setminus} U$
is non-empty, then both $S {\setminus} U$ and $J$
and $J$ are finite.
are finite.
Proof.
(1) Let $A$
 be a right ideal of $S.$
be a right ideal of $S.$ Then $B=(I\times A\times J)\cup \{0\}$
Then $B=(I\times A\times J)\cup \{0\}$ is a right ideal of $T.$
is a right ideal of $T.$ Since $T$
Since $T$ is weakly right noetherian, there exists a finite set $U\subseteq B$
is weakly right noetherian, there exists a finite set $U\subseteq B$ such that $B=UB^{1}.$
such that $B=UB^{1}.$ We may assume that $U=I_0\times X\times J_0$
We may assume that $U=I_0\times X\times J_0$ for some finite sets $I_0\subseteq I,\, X\subseteq A,\, J_0\subseteq J.$
for some finite sets $I_0\subseteq I,\, X\subseteq A,\, J_0\subseteq J.$ We claim that $I=I_0$
We claim that $I=I_0$ and $A=XS^{1}.$
and $A=XS^{1}.$ Indeed, let $i\in I,$
Indeed, let $i\in I,$ $a\in A,$
$a\in A,$ and pick any $j\in J .$
and pick any $j\in J .$ Then $(i,\, a ,\, j)=(i_0,\, x,\, j_0)t$
Then $(i,\, a ,\, j)=(i_0,\, x,\, j_0)t$ for some $(i_0,\, x,\, j_0)\in U$
for some $(i_0,\, x,\, j_0)\in U$ and $t\in T^{1}.$
and $t\in T^{1}.$ It follows that $i=i_0\in I_0$
It follows that $i=i_0\in I_0$ and $a\in xS^{1}\subseteq XS^{1},$
and $a\in xS^{1}\subseteq XS^{1},$ as required.
as required.
(2) Notice that the set $I\times (S {\setminus} U)\times J$
 consists of indecomposable elements of $T$
consists of indecomposable elements of $T$ ; it is hence finite by Lemma 3.10. In particular, both $S {\setminus} U$
; it is hence finite by Lemma 3.10. In particular, both $S {\setminus} U$ and $J$
and $J$ are finite.
are finite.
The converse of Lemma 6.16(1) does not hold in general. In order to show this, we first present the following lemma.
Lemma 6.17 Let $T=\mathcal {M}^{0}(S; I,\, J; P),$![]() let $J^{\prime }$
let $J^{\prime }$![]() be a subset of $J,$
be a subset of $J,$![]() let $P^{\prime }=(p_{ji})_{j\in J^{\prime },\, i\in I}$
let $P^{\prime }=(p_{ji})_{j\in J^{\prime },\, i\in I}$![]() , and let $T^{\prime }=\mathcal {M}^{0}(S; I,\, J^{\prime }; P^{\prime }).$
, and let $T^{\prime }=\mathcal {M}^{0}(S; I,\, J^{\prime }; P^{\prime }).$![]() If $T$
If $T$![]() is weakly right noetherian, then so is $T^{\prime }.$
is weakly right noetherian, then so is $T^{\prime }.$![]()
Proof. It is easy to see that $T^{\prime }$![]() is a right unitary subsemigroup of $T,$
is a right unitary subsemigroup of $T,$![]() so it is weakly right noetherian by Corollary 5.9.
so it is weakly right noetherian by Corollary 5.9.
Example 6.18 Let $T=\mathcal {M}^{0}(S; I,\, J; P)$![]() with $S$
with $S$![]() infinite, and suppose there exists $j\in J$
infinite, and suppose there exists $j\in J$![]() such that $p_{ji}=0$
such that $p_{ji}=0$![]() for all $i\in I.$
for all $i\in I.$![]() Then $T^{\prime }=\mathcal {M}^{0}(S; I,\, \{j\}; P^{\prime }),$
Then $T^{\prime }=\mathcal {M}^{0}(S; I,\, \{j\}; P^{\prime }),$![]() where $P^{\prime }=(p_{ji})_{i\in I},$
where $P^{\prime }=(p_{ji})_{i\in I},$![]() is not weakly right noetherian by Lemma 6.16(2) (in fact, $T^{\prime }$
is not weakly right noetherian by Lemma 6.16(2) (in fact, $T^{\prime }$![]() is an infinite null semigroup). It follows from Lemma 6.17 that $T$
is an infinite null semigroup). It follows from Lemma 6.17 that $T$![]() is not weakly right noetherian.
is not weakly right noetherian.
Remark 6.19 Let $T=\mathcal {M}(S; I,\, J; P)$![]() be a Rees matrix semigroup over an infinite semigroup $S$
be a Rees matrix semigroup over an infinite semigroup $S$![]() with a zero $0$
with a zero $0$![]() adjoined, where $0\notin S.$
adjoined, where $0\notin S.$![]() If there exists $j\in J$
If there exists $j\in J$![]() such that $p_{ji}=0$
such that $p_{ji}=0$![]() for all $i\in I,$
for all $i\in I,$![]() then $T^{\prime }=\mathcal {M}^{0}(S; I,\, J; P)$
then $T^{\prime }=\mathcal {M}^{0}(S; I,\, J; P)$![]() is not weakly right noetherian by Example 6.18. Since $T^{\prime }$
is not weakly right noetherian by Example 6.18. Since $T^{\prime }$![]() is isomorphic to the Rees quotient of $T$
is isomorphic to the Rees quotient of $T$![]() by the ideal $I\times \{0\}\times J,$
by the ideal $I\times \{0\}\times J,$![]() we deduce from Lemma 4.1 that $T$
we deduce from Lemma 4.1 that $T$![]() is not weakly right noetherian.
is not weakly right noetherian.
The converse of Lemma 6.16(1) holds in the case that every row of the matrix contains a unit.
Proposition 6.20 Let $S=\mathcal {M}^{0}(M; I,\, J; P)$![]() be a Rees matrix semigroup over a monoid $M,$
be a Rees matrix semigroup over a monoid $M,$![]() and suppose that for every $j\in J$
and suppose that for every $j\in J$![]() there exists $i\in I$
there exists $i\in I$![]() such that $p_{ji}\in U(M).$
such that $p_{ji}\in U(M).$![]() Then $S$
Then $S$![]() is weakly right noetherian if and only if $M$
is weakly right noetherian if and only if $M$![]() is weakly right noetherian and $I$
is weakly right noetherian and $I$![]() is finite.
is finite.
Proof. The direct implication follows from Lemma 6.16.
For the converse, let $A$![]() be a right ideal of $S.$
be a right ideal of $S.$![]() Note that if $(i,\, u,\, j)\in A,$
Note that if $(i,\, u,\, j)\in A,$![]() then $(i,\, u,\, l)\in A$
then $(i,\, u,\, l)\in A$![]() for all $l\in J.$
for all $l\in J.$![]() Indeed, there exists $k\in I$
Indeed, there exists $k\in I$![]() such that $p_{jk}\in U(M),$
such that $p_{jk}\in U(M),$![]() so $(i,\, u,\, l)=(i,\, u,\, j)(k,\, p_{jk}^{-1},\, l)\in A.$
so $(i,\, u,\, l)=(i,\, u,\, j)(k,\, p_{jk}^{-1},\, l)\in A.$![]() Now fix $j_0\in J,$
Now fix $j_0\in J,$![]() and choose $i_0\in I$
and choose $i_0\in I$![]() such that $p_{j_0i_0}\in U(M).$
such that $p_{j_0i_0}\in U(M).$![]() Let $I^{\prime }$
Let $I^{\prime }$![]() be the set of elements of $I$
be the set of elements of $I$![]() that appear in $A.$
that appear in $A.$![]() For each $i\in I^{\prime },$
For each $i\in I^{\prime },$![]() define a set
define a set
We claim that $A_i$![]() is a right ideal of $S.$
is a right ideal of $S.$![]() Indeed, if $u\in A_i$
Indeed, if $u\in A_i$![]() and $m\in M,$
and $m\in M,$![]() then
then
Since $M$![]() is weakly right noetherian, there exist finite sets $X_i\subseteq A_i,\, i\in I^{\prime },$
is weakly right noetherian, there exist finite sets $X_i\subseteq A_i,\, i\in I^{\prime },$![]() such that $A_i=X_iM.$
such that $A_i=X_iM.$![]() We claim that $A$
We claim that $A$![]() is generated by the finite set
is generated by the finite set
Indeed, if $(i,\, u,\, j)\in A$![]() then $(i,\, u,\, j_0)\in A,$
then $(i,\, u,\, j_0)\in A,$![]() so $u=xm$
so $u=xm$![]() for some $x\in X_i$
for some $x\in X_i$![]() and $m\in M.$
and $m\in M.$![]() Hence, we have $(i,\, u,\, j)=(i,\, x,\, j_0)(i_0,\, p_{j_0i_0}^{-1}m,\, j)\in YM,$
Hence, we have $(i,\, u,\, j)=(i,\, x,\, j_0)(i_0,\, p_{j_0i_0}^{-1}m,\, j)\in YM,$![]() as required.
as required.
Corollary 6.21 Let $S$![]() be a completely (0-)simple semigroup. Then $S$
be a completely (0-)simple semigroup. Then $S$![]() is weakly right noetherian if and only if it has finitely many $\mathcal {R}$
is weakly right noetherian if and only if it has finitely many $\mathcal {R}$![]() -classes.
-classes.
Proof. The semigroup $S^{0}$![]() is completely $0$
is completely $0$![]() -simple. It follows from Proposition 6.20 and Corollary 5.5 that $S$
-simple. It follows from Proposition 6.20 and Corollary 5.5 that $S$![]() is weakly right noetherian if and only if it has finitely many $\mathcal {R}$
is weakly right noetherian if and only if it has finitely many $\mathcal {R}$![]() -classes.
-classes.
We now consider Brandt extensions. Let $S$![]() be a semigroup and let $I$
be a semigroup and let $I$![]() be a non-empty set. The set $(I\times S\times I)\cup \{0\}$
be a non-empty set. The set $(I\times S\times I)\cup \{0\}$![]() becomes a semigroup under the multiplication given by
becomes a semigroup under the multiplication given by

and $0x=x0=0$![]() for all $x\in (I\times S\times I)\cup \{0\}.$
for all $x\in (I\times S\times I)\cup \{0\}.$![]() It is called the Brandt extension of $S$
It is called the Brandt extension of $S$![]() by $I,$
by $I,$![]() and we denote it by $\mathcal {B}(S,\, I).$
and we denote it by $\mathcal {B}(S,\, I).$![]()
Notice that if $S$![]() is a monoid, then $\mathcal {B}(S,\, I)$
is a monoid, then $\mathcal {B}(S,\, I)$![]() is isomorphic to $\mathcal {M}^{0}(S; I,\, I; P)$
is isomorphic to $\mathcal {M}^{0}(S; I,\, I; P)$![]() where $P$
where $P$![]() is the $I\times I$
is the $I\times I$![]() identity matrix. Brandt extensions of groups are precisely the completely $0$
identity matrix. Brandt extensions of groups are precisely the completely $0$![]() -simple inverse semigroups [Reference Petrich23, Theorem V.5.1].
-simple inverse semigroups [Reference Petrich23, Theorem V.5.1].
Proposition 6.22 Let $S$![]() be a semigroup and let $I$
be a semigroup and let $I$![]() be a non-empty set. Then the Brandt extension $\mathcal {B}(S,\, I)$
be a non-empty set. Then the Brandt extension $\mathcal {B}(S,\, I)$![]() is weakly right noetherian if and only if $S$
is weakly right noetherian if and only if $S$![]() is weakly right noetherian and $I$
is weakly right noetherian and $I$![]() is finite.
is finite.
Proof. Let $T=\mathcal {B}(S,\, I).$![]() We just need to prove that if $T$
We just need to prove that if $T$![]() is weakly right noetherian, then $I$
is weakly right noetherian, then $I$![]() is finite. Indeed, if $I$
is finite. Indeed, if $I$![]() is finite, then $\mathcal {B}(S^{1},\, I) {\setminus} T$
is finite, then $\mathcal {B}(S^{1},\, I) {\setminus} T$![]() is finite. It then follows from Corollary 5.5 and Proposition 6.20 that $T$
is finite. It then follows from Corollary 5.5 and Proposition 6.20 that $T$![]() is weakly right noetherian if and only if $S$
is weakly right noetherian if and only if $S$![]() is weakly right noetherian.
is weakly right noetherian.
So, suppose that $T$![]() is weakly right noetherian. Then there exists a finite set $U\subseteq T$
is weakly right noetherian. Then there exists a finite set $U\subseteq T$![]() such that $T=UT^{1}.$
such that $T=UT^{1}.$![]() Let $I_0$
Let $I_0$![]() be the elements of $I$
be the elements of $I$![]() appearing in $U.$
appearing in $U.$![]() Let $i\in I,$
Let $i\in I,$![]() and pick any $s\in S.$
and pick any $s\in S.$![]() Then $(i,\, s,\, i)=(i_1,\, x,\, i_2)t$
Then $(i,\, s,\, i)=(i_1,\, x,\, i_2)t$![]() for some $(i_1,\, x,\, i_2)\in U$
for some $(i_1,\, x,\, i_2)\in U$![]() and $t\in T^{1}.$
and $t\in T^{1}.$![]() It follows that $i=i_1=i_2\in I_0,$
It follows that $i=i_1=i_2\in I_0,$![]() and hence $I=I_0$
and hence $I=I_0$![]() is finite.
is finite.
6.5. Bruck–Reilly extensions
Let $M$![]() be a monoid with identity $1_M$
be a monoid with identity $1_M$![]() and let $\theta : M\to M$
and let $\theta : M\to M$![]() be an endomorphism. We define a binary operation on the set $\mathbb {N}_0\times M\times \mathbb {N}_0$
be an endomorphism. We define a binary operation on the set $\mathbb {N}_0\times M\times \mathbb {N}_0$![]() by
by
where $t=\max (k,\, p)$![]() and $\theta ^{0}$
and $\theta ^{0}$![]() denotes the identity map on $M.$
denotes the identity map on $M.$![]() With this operation the set $\mathbb {N}_0\times M\times \mathbb {N}_0$
With this operation the set $\mathbb {N}_0\times M\times \mathbb {N}_0$![]() is a monoid with identity $(0,\, 1_M,\, 0).$
is a monoid with identity $(0,\, 1_M,\, 0).$![]() It is denoted by $BR(M,\, \theta )$
It is denoted by $BR(M,\, \theta )$![]() and is called the Bruck–Reilly extension of $M$
and is called the Bruck–Reilly extension of $M$![]() determined by $\theta$
determined by $\theta$![]() .
.
The bicyclic monoid is the set $\mathbb {N}_0\times \mathbb {N}_0$![]() with multiplication given by
with multiplication given by
where $t=\max (k,\, p).$![]() Clearly, the bicyclic monoid is a homomorphic image of $BR(M,\, \theta ).$
Clearly, the bicyclic monoid is a homomorphic image of $BR(M,\, \theta ).$![]() We note that the bicyclic monoid is a simple inverse monoid and is defined by the presentation $\langle b,\, c|bc=1\rangle .$
We note that the bicyclic monoid is a simple inverse monoid and is defined by the presentation $\langle b,\, c|bc=1\rangle .$![]() It is well known that every one-sided ideal of the bicyclic monoid is principal, so we certainly have:
It is well known that every one-sided ideal of the bicyclic monoid is principal, so we certainly have:
Lemma 6.23 The bicyclic monoid is weakly noetherian.
We shall provide necessary and sufficient conditions for a Bruck–Reilly extension to be weakly right noetherian. In order to do so, we first make the following definition.
Let $M$![]() be a monoid and let $\theta : M\to M$
be a monoid and let $\theta : M\to M$![]() be an endomorphism. We call a sequence $(I_j)_{j\in \mathbb {N}_0}$
be an endomorphism. We call a sequence $(I_j)_{j\in \mathbb {N}_0}$![]() of right ideals of $M$
of right ideals of $M$![]() a $\theta$
a $\theta$![]() -sequence if $I_j\theta \subseteq I_{j+1}$
-sequence if $I_j\theta \subseteq I_{j+1}$![]() for every $j\geq 0.$
for every $j\geq 0.$![]()
Theorem 6.24 Let $M$![]() be a monoid and let $\theta : M\to M$
be a monoid and let $\theta : M\to M$![]() be an endomorphism. Then $BR(M,\, \theta )$
be an endomorphism. Then $BR(M,\, \theta )$![]() is weakly right noetherian if and only if the following conditions hold$:$
is weakly right noetherian if and only if the following conditions hold$:$![]()
(1) $M$
 is weakly right noetherian$;$
is weakly right noetherian$;$
(2) for any $\theta$
 -sequence $(I_j)_{j\in \mathbb {N}_0}$
-sequence $(I_j)_{j\in \mathbb {N}_0}$ of right ideals of $M,$
of right ideals of $M,$ there exists some $n\in \mathbb {N}_0$
there exists some $n\in \mathbb {N}_0$ with a finite set $Y\subseteq I_n$
with a finite set $Y\subseteq I_n$ such that $I_{n+r}=(Y\theta ^{r})M$
such that $I_{n+r}=(Y\theta ^{r})M$ for all $r\geq 0.$
for all $r\geq 0.$
Proof. We denote $BR(M,\, \theta )$![]() by $N.$
by $N.$![]() Note that for any right ideal $I$
Note that for any right ideal $I$![]() of $N,$
of $N,$![]() we have $(j,\, a,\, k)\in I$
we have $(j,\, a,\, k)\in I$![]() if and only if $(j,\, a,\, 0)\in I.$
if and only if $(j,\, a,\, 0)\in I.$![]()
($\Rightarrow$![]() ) The monoid $M$
) The monoid $M$![]() is isomorphic to the submonoid $M_0=\{0\}\times M\times \{0\}$
is isomorphic to the submonoid $M_0=\{0\}\times M\times \{0\}$![]() of $N.$
of $N.$![]() It can easily be shown $M_0$
It can easily be shown $M_0$![]() is right unitary in $N,$
is right unitary in $N,$![]() so $M\cong M_0$
so $M\cong M_0$![]() is weakly right noetherian by Corollary 5.9.
is weakly right noetherian by Corollary 5.9.
Now let $(I_j)_{j\in \mathbb {N}_0}$![]() be a $\theta$
be a $\theta$![]() -sequence of right ideals of $M.$
-sequence of right ideals of $M.$![]() We define a set
We define a set
We claim that $I$![]() is a right ideal of $N.$
is a right ideal of $N.$![]() Indeed, let $(j,\, a,\, k)\in I$
Indeed, let $(j,\, a,\, k)\in I$![]() and $(p,\, m,\, q)\in N.$
and $(p,\, m,\, q)\in N.$![]() Then $A\in I_j.$
Then $A\in I_j.$![]() Let $u$
Let $u$![]() denote the element
denote the element
where $t=\max (k,\, p).$![]() If $t=k,$
If $t=k,$![]() then $u=(j,\, a(m\theta ^{k-p}),\, q-p+k)\in I$
then $u=(j,\, a(m\theta ^{k-p}),\, q-p+k)\in I$![]() since $I_j$
since $I_j$![]() is a right ideal of $M.$
is a right ideal of $M.$![]() If $t=p,$
If $t=p,$![]() then $u=(j-k+p,\, (a\theta ^{p-k})m,\, q)\in I,$
then $u=(j-k+p,\, (a\theta ^{p-k})m,\, q)\in I,$![]() since $(a\theta ^{p-k})\in I_{j-k+p}$
since $(a\theta ^{p-k})\in I_{j-k+p}$![]() and $I_{j-k+p}$
and $I_{j-k+p}$![]() is a right ideal of $M.$
is a right ideal of $M.$![]()
Since $N$![]() is weakly right noetherian, there exists a finite set $X\subseteq I$
is weakly right noetherian, there exists a finite set $X\subseteq I$![]() such that $I=XN.$
such that $I=XN.$![]() By the note given at the beginning of the proof, we may assume that the third coordinate of each element of $X$
By the note given at the beginning of the proof, we may assume that the third coordinate of each element of $X$![]() is $0.$
is $0.$![]() Set $n=\max \{j : (j,\, a,\, 0)\in X\},$
Set $n=\max \{j : (j,\, a,\, 0)\in X\},$![]() and let
and let
Let $r\geq 0$![]() and let $b\in I_{n+r}.$
and let $b\in I_{n+r}.$![]() Then $(n+r,\, b,\, 0)\in I,$
Then $(n+r,\, b,\, 0)\in I,$![]() so there exist $(j,\, a,\, 0)\in X$
so there exist $(j,\, a,\, 0)\in X$![]() and $(p,\, m,\, q)\in N$
and $(p,\, m,\, q)\in N$![]() such that $(n+r,\, b,\, 0)=(j,\, a,\, 0)(p,\, m,\, q).$
such that $(n+r,\, b,\, 0)=(j,\, a,\, 0)(p,\, m,\, q).$![]() It follows that $n+r=j+p,$
It follows that $n+r=j+p,$![]() $b=(a\theta ^{p})m$
$b=(a\theta ^{p})m$![]() and $q=0.$
and $q=0.$![]() Hence, we have that
Hence, we have that
so $I_{n+r}=(Y\theta ^{r})M,$![]() as required.
as required.
($\Leftarrow$![]() ) Let $I$
) Let $I$![]() be a right ideal of $N.$
be a right ideal of $N.$![]() For each $j\in \mathbb {N}_0$
For each $j\in \mathbb {N}_0$![]() define a set
define a set
Clearly, $I_j$![]() is either empty or a right ideal of $N.$
is either empty or a right ideal of $N.$![]() Let $n_0$
Let $n_0$![]() be minimal such that $I_{n_0}$
be minimal such that $I_{n_0}$![]() is non-empty. For any $j\geq n_0,$
is non-empty. For any $j\geq n_0,$![]() we have
we have
so $I_j\theta \subseteq I_{j+1}.$![]() Thus $(I_j)_{j\geq n_0}$
Thus $(I_j)_{j\geq n_0}$![]() is a $\theta$
is a $\theta$![]() -sequence of right ideals of $M.$
-sequence of right ideals of $M.$![]() By assumption, there exists $n\geq n_0$
By assumption, there exists $n\geq n_0$![]() with a finite set $Y\subseteq I_n$
with a finite set $Y\subseteq I_n$![]() such that $I_{n+r}=(Y\theta ^{r})M$
such that $I_{n+r}=(Y\theta ^{r})M$![]() for all $r\geq 0.$
for all $r\geq 0.$![]() Since $M$
Since $M$![]() is weakly right noetherian, for each $j\in \{n_0,\, \ldots ,\, n-1\}$
is weakly right noetherian, for each $j\in \{n_0,\, \ldots ,\, n-1\}$![]() there exists a finite set $X_j\subseteq I_j$
there exists a finite set $X_j\subseteq I_j$![]() such that $I_j=X_jM.$
such that $I_j=X_jM.$![]() Writing $Y=X_n,$
Writing $Y=X_n,$![]() we claim that $I$
we claim that $I$![]() is generated by the finite set
is generated by the finite set

Let $(j,\, a,\, k)\in I.$![]() Then $a\in I_j$
Then $a\in I_j$![]() and $j\geq n_0.$
and $j\geq n_0.$![]() If $j< n,$
If $j< n,$![]() then $a=xm$
then $a=xm$![]() for some $x\in X_j$
for some $x\in X_j$![]() and $m\in M,$
and $m\in M,$![]() so we have
so we have
If $j\geq n,$![]() then $a=(x\theta ^{j-n})m$
then $a=(x\theta ^{j-n})m$![]() for some $x\in X_n$
for some $x\in X_n$![]() and $m\in M,$
and $m\in M,$![]() and hence
and hence
as required.
Corollary 6.25 Let $M$![]() be a monoid and let $\theta : M\to U(M)$
be a monoid and let $\theta : M\to U(M)$![]() be a homomorphism. Then $BR(M,\, \theta )$
be a homomorphism. Then $BR(M,\, \theta )$![]() is weakly right noetherian if and only if $M$
is weakly right noetherian if and only if $M$![]() is weakly right noetherian.
is weakly right noetherian.
Proof. The forward direction follows immediately from Theorem 6.24. For the converse, let $(I_j)_{j\in \mathbb {N}_0}$![]() be a $\theta$
be a $\theta$![]() -sequence of right ideals of $M.$
-sequence of right ideals of $M.$![]() For any $j\in \mathbb {N}_0,$
For any $j\in \mathbb {N}_0,$![]() we have $I_j\theta \in U(M)$
we have $I_j\theta \in U(M)$![]() and $I_j\theta \subseteq I_{j+1},$
and $I_j\theta \subseteq I_{j+1},$![]() so $I_{j+1}\cap U(M)\neq \emptyset .$
so $I_{j+1}\cap U(M)\neq \emptyset .$![]() Since $I_{j+1}$
Since $I_{j+1}$![]() is a right ideal of $M,$
is a right ideal of $M,$![]() it follows that $I_{j+1}=M.$
it follows that $I_{j+1}=M.$![]() Thus $M=I_1=I_2=\cdots$
Thus $M=I_1=I_2=\cdots$![]() , and $I_{1+r}=(\{1_M\}\theta ^{r})M$
, and $I_{1+r}=(\{1_M\}\theta ^{r})M$![]() for all $r\geq 0.$
for all $r\geq 0.$![]() Hence, $BR(M,\, \theta )$
Hence, $BR(M,\, \theta )$![]() is weakly right noetherian by Theorem 6.24.
is weakly right noetherian by Theorem 6.24.
We deduce from Theorem 6.24 that the Bruck–Reilly extension of a weakly right noetherian monoid (indeed, even a finite monoid) need not be weakly right noetherian.
Lemma 6.26 Let $M$![]() be a monoid. Suppose there exists a right ideal $I$
be a monoid. Suppose there exists a right ideal $I$![]() of $M,$
of $M,$![]() an element $a\in M {\setminus} I,$
an element $a\in M {\setminus} I,$![]() and a monoid homomorphism $\theta : M\to M$
and a monoid homomorphism $\theta : M\to M$![]() such that $(I\cup \{a\})\theta \subseteq I.$
such that $(I\cup \{a\})\theta \subseteq I.$![]() Then $BR(M,\, \theta )$
Then $BR(M,\, \theta )$![]() is not weakly right noetherian.
is not weakly right noetherian.
Proof. Let $J$![]() be the right ideal $aM\cup I,$
be the right ideal $aM\cup I,$![]() and consider the infinite $\theta$
and consider the infinite $\theta$![]() -sequence $J,\, J,\, \ldots .$
-sequence $J,\, J,\, \ldots .$![]() Since $J\theta \subseteq I\subsetneq J,$
Since $J\theta \subseteq I\subsetneq J,$![]() this sequence does not satisfy the condition in (2) of Theorem 6.24, so $BR(M,\, \theta )$
this sequence does not satisfy the condition in (2) of Theorem 6.24, so $BR(M,\, \theta )$![]() is not weakly right noetherian.
is not weakly right noetherian.
Remark 6.27 The condition of Lemma 6.26 is satisfied by the bicyclic monoid: let $a=(1,\, 0),$![]() let $I=(2,\, 0)B,$
let $I=(2,\, 0)B,$![]() and let $\theta : B\to B$
and let $\theta : B\to B$![]() be given by $(i,\, j)\theta =(2i,\, 2j).$
be given by $(i,\, j)\theta =(2i,\, 2j).$![]()
This condition is also satisfied by any monoid $M$![]() such that $M {\setminus} U(M)$
such that $M {\setminus} U(M)$![]() is an ideal containing an idempotent $e$
is an ideal containing an idempotent $e$![]() and an element $a\notin eM$
and an element $a\notin eM$![]() (e.g. the 2-element null semigroup with an identity adjoined). Indeed, let $I=eM$
(e.g. the 2-element null semigroup with an identity adjoined). Indeed, let $I=eM$![]() and let $\theta : M\to M$
and let $\theta : M\to M$![]() be the endomorphism given by $U(M)\theta =\{1\}$
be the endomorphism given by $U(M)\theta =\{1\}$![]() and $\bigl (M {\setminus} U(M)\bigr )\theta =\{e\}.$
and $\bigl (M {\setminus} U(M)\bigr )\theta =\{e\}.$![]() Then $(I\cup \{a\})\theta =\{e\}\subseteq I.$
Then $(I\cup \{a\})\theta =\{e\}\subseteq I.$![]()
7. Regular semigroups
In this section, we study weakly right noetherian regular semigroups. We begin with a necessary and sufficient condition for a regular semigroup to be weakly right noetherian. We then focus our attention on certain classes of regular semigroups, including inverse semigroups, completely regular semigroups and regular semigroups with a principal series.
Theorem 7.1 The following are equivalent for a regular semigroup $S$![]() :
:
(1) $S$
 is weakly right noetherian;
is weakly right noetherian;(2) for every subset $U\subseteq E(S),$
 there exists a finite set $X\subseteq U$
there exists a finite set $X\subseteq U$ with the following property: for each $u\in U$
with the following property: for each $u\in U$ there exists $x\in X$
there exists $x\in X$ such that $u=xu$
such that $u=xu$ .
.
Proof. $(1)\Rightarrow (2)$![]() . Let $U$
. Let $U$![]() be a subset of $E(S),$
be a subset of $E(S),$![]() and let $I$
and let $I$![]() be the right ideal $US^{1}$
be the right ideal $US^{1}$![]() of $S.$
of $S.$![]() Since $S$
Since $S$![]() is weakly right noetherian, there exists a finite subset $X\subseteq U$
is weakly right noetherian, there exists a finite subset $X\subseteq U$![]() such that $I=XS^{1}.$
such that $I=XS^{1}.$![]() For each $u\in U,$
For each $u\in U,$![]() we have that $u=xs$
we have that $u=xs$![]() for some $x\in X$
for some $x\in X$![]() and $s\in S^{1},$
and $s\in S^{1},$![]() and hence $u=x^{2}s=xu.$
and hence $u=x^{2}s=xu.$![]()
$(2)\Leftarrow (1).$![]() Let $I$
Let $I$![]() be a right ideal of $S.$
be a right ideal of $S.$![]() By assumption, there exists a finite set $X\subseteq I\cap E(S)$
By assumption, there exists a finite set $X\subseteq I\cap E(S)$![]() satisfying the property in (2). We claim that $I=XS.$
satisfying the property in (2). We claim that $I=XS.$![]() Indeed, let $a\in I.$
Indeed, let $a\in I.$![]() Let $b$
Let $b$![]() be an inverse of $a,$
be an inverse of $a,$![]() so $a=aba.$
so $a=aba.$![]() Then $ab\in I\cap E(S),$
Then $ab\in I\cap E(S),$![]() so there exists $x\in X$
so there exists $x\in X$![]() such that $ab=x(ab)$
such that $ab=x(ab)$![]() . Thus $a=aba=xa\in XS,$
. Thus $a=aba=xa\in XS,$![]() as required.
as required.
Let $S$![]() be a regular semigroup, and let $T=\langle E(S)\rangle$
be a regular semigroup, and let $T=\langle E(S)\rangle$![]() be the subsemigroup of $S$
be the subsemigroup of $S$![]() generated by its set of idempotents. Then $T$
generated by its set of idempotents. Then $T$![]() is regular by [Reference Fitz-Gerald7, Corollary 2]. Since $E(S)=E(T),$
is regular by [Reference Fitz-Gerald7, Corollary 2]. Since $E(S)=E(T),$![]() we immediate deduce from Theorem 7.1:
we immediate deduce from Theorem 7.1:
Corollary 7.2 A regular semigroup $S$![]() is weakly right noetherian if and only if its subsemigroup $T=\langle E(S)\rangle$
is weakly right noetherian if and only if its subsemigroup $T=\langle E(S)\rangle$![]() is weakly right noetherian.
is weakly right noetherian.
Corollary 7.3 An inverse semigroup $S$![]() is weakly right noetherian if and only if its semilattice of idempotents $E(S)$
is weakly right noetherian if and only if its semilattice of idempotents $E(S)$![]() is weakly noetherian.
is weakly noetherian.
Corollary 7.4 An inverse semigroup is weakly right noetherian if and only if it is weakly noetherian.
Remark 7.5 Corollary 7.4 does not hold for regular semigoups in general. Indeed, any infinite right zero semigroup is weakly right noetherian but not weakly left noetherian.
Let $X$![]() be an infinite set, and let $X^{-1}=\{x^{-1} : x\in X\}$
be an infinite set, and let $X^{-1}=\{x^{-1} : x\in X\}$![]() be a set disjoint from $X.$
be a set disjoint from $X.$![]() The polycyclic monoid over $X,$
The polycyclic monoid over $X,$![]() denoted by $P_X,$
denoted by $P_X,$![]() is the monoid with zero defined by the presentation
is the monoid with zero defined by the presentation
This presentation yields the normal form $\{u^{-1}v : u,\, v\in X^{*}\}\cup \{0\}$![]() for $P_X$
for $P_X$![]() [Reference Meakin and Sapir19, Section 1]. The monoid $P_X$
[Reference Meakin and Sapir19, Section 1]. The monoid $P_X$![]() is an inverse monoid with a single non-zero $\mathcal {D}$
is an inverse monoid with a single non-zero $\mathcal {D}$![]() -class (see [Reference Perrot22, Section 1.3] or [Reference Campbell, Quick, Robertson and Smith2, p. 478]). In the case that $|X|=1,$
-class (see [Reference Perrot22, Section 1.3] or [Reference Campbell, Quick, Robertson and Smith2, p. 478]). In the case that $|X|=1,$![]() $P_X$
$P_X$![]() is the bicyclic monoid with zero adjoined. It turns out that this is the only case where $P_X$
is the bicyclic monoid with zero adjoined. It turns out that this is the only case where $P_X$![]() is weakly noetherian.
is weakly noetherian.
Proposition 7.6 The polycyclic monoid $P_X$![]() is weakly noetherian if and only if $|X|=1$
is weakly noetherian if and only if $|X|=1$![]() .
.
Proof. If $|X|=1,$![]() then $P_X$
then $P_X$![]() is weakly noetherian by Lemma 6.23 and Corollaries 5.5 and 7.4.
is weakly noetherian by Lemma 6.23 and Corollaries 5.5 and 7.4.
Suppose $|X|\geq 2.$![]() Choose distinct elements $x,\, y\in X.$
Choose distinct elements $x,\, y\in X.$![]() We claim that the infinite set $\{y^{-i}x^{-1}xy^{i} : i\in \mathbb {N}\}\subseteq E(P_X)$
We claim that the infinite set $\{y^{-i}x^{-1}xy^{i} : i\in \mathbb {N}\}\subseteq E(P_X)$![]() is an antichain. Indeed, since $xy^{-1}=yx^{-1}=0,$
is an antichain. Indeed, since $xy^{-1}=yx^{-1}=0,$![]() we deduce that for any $i\neq j,$
we deduce that for any $i\neq j,$![]()
It now follows from Proposition 6.6 that $E(P_X)$![]() is not weakly noetherian, and hence $P_X$
is not weakly noetherian, and hence $P_X$![]() is not weakly noetherian by Corollary 7.3.
is not weakly noetherian by Corollary 7.3.
We now show that the principal factors of a regular semigroup inherit the property of being weakly right noetherian.
Lemma 7.7 Let $S$![]() be a regular semigroup. If $S$
be a regular semigroup. If $S$![]() is weakly right noetherian, then so are all its principal factors.
is weakly right noetherian, then so are all its principal factors.
Proof. Let $J$![]() be a $\mathcal {J}$
be a $\mathcal {J}$![]() -class of $S,$
-class of $S,$![]() fix $x\in J,$
fix $x\in J,$![]() and let $T=S^{1}xS^{1}.$
and let $T=S^{1}xS^{1}.$![]() Now, $T$
Now, $T$![]() is a union of $\mathcal {J}$
is a union of $\mathcal {J}$![]() -classes of $S,$
-classes of $S,$![]() of which $J$
of which $J$![]() is the unique maximal one. Since any pair of elements of $S$
is the unique maximal one. Since any pair of elements of $S$![]() that are inverses of each other must belong to the same $\mathcal {J}$
that are inverses of each other must belong to the same $\mathcal {J}$![]() -class, it follows that $T$
-class, it follows that $T$![]() is regular, and hence $T$
is regular, and hence $T$![]() is weakly right noetherian by Corollary 5.7. Then the principal factor of $J$
is weakly right noetherian by Corollary 5.7. Then the principal factor of $J$![]() is weakly right noetherian by Lemma 4.1, since it is a Rees quotient of $T.$
is weakly right noetherian by Lemma 4.1, since it is a Rees quotient of $T.$![]()
Lemma 7.7 and Corollary 4.8 together yield:
Corollary 7.8 Let $S$![]() be a regular semigroup with a principal series. Then $S$
be a regular semigroup with a principal series. Then $S$![]() is weakly right noetherian if and only if all its principal factors are weakly right noetherian.
is weakly right noetherian if and only if all its principal factors are weakly right noetherian.
A semigroup $S$![]() is said to be completely semisimple if all its principal factors are completely $0$
is said to be completely semisimple if all its principal factors are completely $0$![]() -simple or completely simple.
-simple or completely simple.
Corollary 7.9 Let $S$![]() be a completely semisimple semigroup with a principal series. Then $S$
be a completely semisimple semigroup with a principal series. Then $S$![]() is weakly right noetherian if and only if it has finitely many $\mathcal {R}$
is weakly right noetherian if and only if it has finitely many $\mathcal {R}$![]() -classes.
-classes.
Proof. If $S$![]() is weakly right noetherian, then every principal factor of $S$
is weakly right noetherian, then every principal factor of $S$![]() has finitely many $\mathcal {R}$
has finitely many $\mathcal {R}$![]() -classes by Lemma 7.8 and Corollary 6.21. It follows that every $\mathcal {J}$
-classes by Lemma 7.8 and Corollary 6.21. It follows that every $\mathcal {J}$![]() -class is a finite union of $\mathcal {R}$
-class is a finite union of $\mathcal {R}$![]() -classes. Since $S$
-classes. Since $S$![]() has finitely many $\mathcal {J}$
has finitely many $\mathcal {J}$![]() -classes, we conclude that it has finitely many $\mathcal {R}$
-classes, we conclude that it has finitely many $\mathcal {R}$![]() -classes.
-classes.
The converse follows from Corollary 3.3.
Remark 7.10 Corollary 7.9 does not hold is we remove the condition that $S$![]() has a principal series. Indeed, there exist infinite weakly noetherian semilattices (in which $\mathcal {J}=\mathcal {R}$
has a principal series. Indeed, there exist infinite weakly noetherian semilattices (in which $\mathcal {J}=\mathcal {R}$![]() is the identity relation).
is the identity relation).
Also, Corollary 7.9 does not hold for general regular semigroups with a principal series. For example, the bicyclic monoid has a single $J$![]() -class and is weakly right noetherian, but it has infinitely many $\mathcal {R}$
-class and is weakly right noetherian, but it has infinitely many $\mathcal {R}$![]() -classes.
-classes.
A semigroup is said to be completely regular if it is a union of groups. Completely regular semigroups have the following characterization.
Theorem 7.11 Howie [Reference Howie13, Theorem 4.1.3]
Every completely regular semigroup is a semilattice of completely simple semigroups.
From Lemmas 6.7 and 6.11, and Corollary 6.21, we deduce:
Proposition 7.12 Let $S$![]() be a completely regular semigroup, and let $S=\mathcal {S}(Y,\, S_{\alpha })$
be a completely regular semigroup, and let $S=\mathcal {S}(Y,\, S_{\alpha })$![]() be its decomposition into a semilattice of completely simple semigroups. If $S$
be its decomposition into a semilattice of completely simple semigroups. If $S$![]() is weakly right noetherian, then $Y$
is weakly right noetherian, then $Y$![]() is weakly noetherian and each $S_{\alpha }$
is weakly noetherian and each $S_{\alpha }$![]() has finitely many $\mathcal {R}$
has finitely many $\mathcal {R}$![]() -classes.
-classes.
We shall see that the converse of Proposition 7.12 does not hold.
In the remainder of this section, we focus our attention on strong semilattices of completely simple semigroups. For more information about the structure of such semigroups, see [Reference Petrich23, Section IV.4].
A Clifford semigroup is an inverse completely regular semigroup. It follows from Theorem 7.11 that Clifford semigroups are precisely the semilattices of groups. In fact, Clifford semigroups are strong semilattices of groups [Reference Grillet11, Theorem III.2.12]. If $S=\mathcal {S}(Y,\, G_{\alpha })$![]() is a semilattice of groups, it is clear that $Y$
is a semilattice of groups, it is clear that $Y$![]() is isomorphic to $E(S)$
is isomorphic to $E(S)$![]() , so Corollary 7.3 yields:
, so Corollary 7.3 yields:
Corollary 7.13 Let $S$![]() be a Clifford semigroup with decomposition $S=\mathcal {S}(Y,\, G_{\alpha })$
be a Clifford semigroup with decomposition $S=\mathcal {S}(Y,\, G_{\alpha })$![]() into a semilattice of groups. Then $S$
into a semilattice of groups. Then $S$![]() is weakly right noetherian if and only if $Y$
is weakly right noetherian if and only if $Y$![]() is weakly noetherian.
is weakly noetherian.
In what follows we shall provide necessary and sufficient conditions for a general strong semilattice of completely simple semigroups to be weakly right noetherian. We use the following folklore result, which we prove for completeness.
Lemma 7.14 Let $S=\mathcal {S}(Y,\, S_{\alpha },\, \phi _{\alpha , \beta })$![]() be a strong semilattice of completely simple semigroups. Then each of Green's relations is a congruence on $S.$
be a strong semilattice of completely simple semigroups. Then each of Green's relations is a congruence on $S.$![]() Furthermore, we have $S/\mathcal {J}=S/\mathcal {D}=Y$
Furthermore, we have $S/\mathcal {J}=S/\mathcal {D}=Y$![]() ; $S/\mathcal {R}$
; $S/\mathcal {R}$![]() is a strong semilattice of left zero semigroups; $S/\mathcal {L}$
is a strong semilattice of left zero semigroups; $S/\mathcal {L}$![]() is a strong semilattice of right zero semigroups; and $S/\mathcal {H}$
is a strong semilattice of right zero semigroups; and $S/\mathcal {H}$![]() is a strong semilattice of rectangular bands.
is a strong semilattice of rectangular bands.
Proof. It is clear that $\mathcal {D}=\mathcal {J}$![]() and $S/\mathcal {J}=Y.$
and $S/\mathcal {J}=Y.$![]() We prove that $\mathcal {R}$
We prove that $\mathcal {R}$![]() is a congruence. A dual argument proves that $\mathcal {L}$
is a congruence. A dual argument proves that $\mathcal {L}$![]() is a congruence, and hence $\mathcal {H}=\mathcal {R}\cap \mathcal {L}$
is a congruence, and hence $\mathcal {H}=\mathcal {R}\cap \mathcal {L}$![]() is congruence.
is congruence.
For each $\alpha \in Y,$![]() let $S_{\alpha }=\mathcal {M}(G_{\alpha }; I_{\alpha },\, J_{\alpha }; P_{\alpha }).$
let $S_{\alpha }=\mathcal {M}(G_{\alpha }; I_{\alpha },\, J_{\alpha }; P_{\alpha }).$![]() Recall that $\mathcal {R}$
Recall that $\mathcal {R}$![]() is a left congruence on $S,$
is a left congruence on $S,$![]() so we just need to show that it is a right congruence. For $\alpha \in Y,$
so we just need to show that it is a right congruence. For $\alpha \in Y,$![]() we write $\mathcal {R}_{\alpha }=\mathcal {R}_{S_{\alpha }}.$
we write $\mathcal {R}_{\alpha }=\mathcal {R}_{S_{\alpha }}.$![]() Since $S_{\alpha }$
Since $S_{\alpha }$![]() is regular, we have that $\mathcal {R}_{\alpha }=\mathcal {R}\cap (S_{\alpha }\times S_{\alpha })$
is regular, we have that $\mathcal {R}_{\alpha }=\mathcal {R}\cap (S_{\alpha }\times S_{\alpha })$![]() [Reference Howie13, Proposition 2.4.2]. Note that $\mathcal {R}_{\alpha }$
[Reference Howie13, Proposition 2.4.2]. Note that $\mathcal {R}_{\alpha }$![]() is a congruence on $S_{\alpha }$
is a congruence on $S_{\alpha }$![]() .
.
Let $(a,\, b)\in \mathcal {R}$![]() and $c\in S.$
and $c\in S.$![]() Since $Y$
Since $Y$![]() is $\mathcal {R}$
is $\mathcal {R}$![]() -trivial, we must have that $(a,\, b)\in \mathcal {R}_{\alpha }$
-trivial, we must have that $(a,\, b)\in \mathcal {R}_{\alpha }$![]() for some $\alpha \in Y.$
for some $\alpha \in Y.$![]() Now, the element $c$
Now, the element $c$![]() belongs to some $S_{\beta },\, \beta \in Y.$
belongs to some $S_{\beta },\, \beta \in Y.$![]() Certainly $(a\phi _{\alpha , \alpha \beta },\, b\phi _{\alpha , \alpha \beta })\in \mathcal {R}_{\alpha \beta }.$
Certainly $(a\phi _{\alpha , \alpha \beta },\, b\phi _{\alpha , \alpha \beta })\in \mathcal {R}_{\alpha \beta }.$![]() Since $\mathcal {R}_{\alpha \beta }$
Since $\mathcal {R}_{\alpha \beta }$![]() is a congruence, we have
is a congruence, we have
as required.
It can be easily shown that $S/\mathcal {R}\cong \mathcal {S}(Y,\, I_{\alpha },\, \psi _{\alpha , \beta }),$![]() where the $I_{\alpha }$
where the $I_{\alpha }$![]() are considered as left zero semigroups and each $\psi _{\alpha , \beta } : I_{\alpha }\to I_{\beta }$
are considered as left zero semigroups and each $\psi _{\alpha , \beta } : I_{\alpha }\to I_{\beta }$![]() is defined as follows: $i_{\alpha }\psi _{\alpha , \beta }=k_{\beta }$
is defined as follows: $i_{\alpha }\psi _{\alpha , \beta }=k_{\beta }$![]() if for some (and hence all) $j_{\alpha }\in J_{\alpha },$
if for some (and hence all) $j_{\alpha }\in J_{\alpha },$![]() we have
we have
for some $l_{\beta }\in J_{\beta }.$![]() Dually, we have that $S/\mathcal {L}$
Dually, we have that $S/\mathcal {L}$![]() is a strong semilattice of right zero semigroups. Finally, we have $S/\mathcal {H}\cong \mathcal {S}(Y,\, B_{\alpha },\, \theta _{\alpha , \beta }),$
is a strong semilattice of right zero semigroups. Finally, we have $S/\mathcal {H}\cong \mathcal {S}(Y,\, B_{\alpha },\, \theta _{\alpha , \beta }),$![]() where each $B_{\alpha }=I_{\alpha }\times J_{\alpha }$
where each $B_{\alpha }=I_{\alpha }\times J_{\alpha }$![]() is a rectangular band and each $\theta _{\alpha , \beta } : B_{\alpha }\to B_{\beta }$
is a rectangular band and each $\theta _{\alpha , \beta } : B_{\alpha }\to B_{\beta }$![]() is defined as follows: $(i_{\alpha },\, j_{\alpha })\theta _{\alpha , \beta }=(k_{\beta },\, l_{\beta })$
is defined as follows: $(i_{\alpha },\, j_{\alpha })\theta _{\alpha , \beta }=(k_{\beta },\, l_{\beta })$![]() if
if
This completes the proof.
Theorem 7.15 Let $S$![]() be a strong semilattice of completely simple semigroups, and let $S/\mathcal {R}=\mathcal {S}(Y,\, S_{\alpha },\, \phi _{\alpha , \beta })$
be a strong semilattice of completely simple semigroups, and let $S/\mathcal {R}=\mathcal {S}(Y,\, S_{\alpha },\, \phi _{\alpha , \beta })$![]() be the decomposition of $S/\mathcal{R}$
be the decomposition of $S/\mathcal{R}$![]() into a strong semilattice of left zero semigroups. Then $S$
into a strong semilattice of left zero semigroups. Then $S$![]() is weakly right noetherian if and only if the following conditions hold:
is weakly right noetherian if and only if the following conditions hold:
(1) $Y$
 is weakly noetherian;
is weakly noetherian;(2) each $S_{\alpha }$
 is finite;
is finite;(3) there exists a finite subsemilattice $Y_0$
 of $Y$
of $Y$ with the following property: for each $\beta \in Y,$
with the following property: for each $\beta \in Y,$ there exists $\alpha \in Y_0$
there exists $\alpha \in Y_0$ such that $\alpha \geq \beta$
such that $\alpha \geq \beta$ and $\phi _{\alpha , \beta }$
and $\phi _{\alpha , \beta }$ is surjective.
is surjective.
Proof. Green's relation $\mathcal {R}$![]() is a congruence on $S$
is a congruence on $S$![]() by Lemma 7.14. Hence, by Lemma 4.3, $S$
by Lemma 7.14. Hence, by Lemma 4.3, $S$![]() is weakly right noetherian if and only if $S/\mathcal {R}$
is weakly right noetherian if and only if $S/\mathcal {R}$![]() is weakly right noetherian. Therefore, it suffices to consider the case that $S=S/\mathcal {R}.$
is weakly right noetherian. Therefore, it suffices to consider the case that $S=S/\mathcal {R}.$![]()
($\Rightarrow$![]() ) (1) and (2) follow immediately from Proposition 7.12. For (3), we have that $S=XS$
) (1) and (2) follow immediately from Proposition 7.12. For (3), we have that $S=XS$![]() for some finite subset $X\subseteq S.$
for some finite subset $X\subseteq S.$![]() Let $Y_0$
Let $Y_0$![]() be the semigroup generated by $\{\alpha \in Y : X\cap S_{\alpha }\neq \emptyset \}.$
be the semigroup generated by $\{\alpha \in Y : X\cap S_{\alpha }\neq \emptyset \}.$![]() Since $X$
Since $X$![]() is finite and $Y$
is finite and $Y$![]() is locally finite (that is, every finitely generated subsemigroup is finite), we conclude that $Y_0$
is locally finite (that is, every finitely generated subsemigroup is finite), we conclude that $Y_0$![]() is finite.
is finite.
Now consider $\beta \in Y,$![]() and let $S_{\beta }=\{b_1,\, \ldots ,\, b_n\}.$
and let $S_{\beta }=\{b_1,\, \ldots ,\, b_n\}.$![]() For each $i\in \{1,\, \ldots ,\, n\},$
For each $i\in \{1,\, \ldots ,\, n\},$![]() there exists $x_i\in X$
there exists $x_i\in X$![]() such that $b_i\in x_iS,$
such that $b_i\in x_iS,$![]() which implies that $b_i=x_ib_i.$
which implies that $b_i=x_ib_i.$![]() Let $x_i\in S_{\alpha _i}.$
Let $x_i\in S_{\alpha _i}.$![]() Since $S_{\beta }$
Since $S_{\beta }$![]() is a left zero semigroup, we have $b_i=(x_i\phi _{\alpha _i, \beta })b_i=x_i\phi _{\alpha _i, \beta }.$
is a left zero semigroup, we have $b_i=(x_i\phi _{\alpha _i, \beta })b_i=x_i\phi _{\alpha _i, \beta }.$![]() Now set $\alpha =\alpha _1\cdots \alpha _n.$
Now set $\alpha =\alpha _1\cdots \alpha _n.$![]() Then $\alpha \in Y_0,$
Then $\alpha \in Y_0,$![]() and since $\alpha _i\geq \beta$
and since $\alpha _i\geq \beta$![]() for all $i\in \{1,\, \ldots ,\, n\},$
for all $i\in \{1,\, \ldots ,\, n\},$![]() we deduce that $\alpha \geq \beta .$
we deduce that $\alpha \geq \beta .$![]() For each $i\in \{1,\, \ldots ,\, n\},$
For each $i\in \{1,\, \ldots ,\, n\},$![]() we have $b_i=(x_i\phi _{\alpha _i, \alpha })\phi _{\alpha , \beta },$
we have $b_i=(x_i\phi _{\alpha _i, \alpha })\phi _{\alpha , \beta },$![]() so $\phi _{\alpha , \beta }$
so $\phi _{\alpha , \beta }$![]() is surjective.
is surjective.
($\Leftarrow$![]() ) Let $I$
) Let $I$![]() be a right ideal of $S.$
be a right ideal of $S.$![]() For each $\alpha \in Y_0$
For each $\alpha \in Y_0$![]() and $a\in S_{\alpha },$
and $a\in S_{\alpha },$![]() define a set
define a set
and let $I_a$![]() be the right ideal $U_aY$
be the right ideal $U_aY$![]() of $Y.$
of $Y.$![]() Since $Y$
Since $Y$![]() is weakly noetherian, there exists a finite set $X_a\subseteq U_a$
is weakly noetherian, there exists a finite set $X_a\subseteq U_a$![]() such that $I_a=X_aY.$
such that $I_a=X_aY.$![]() We claim that $I$
We claim that $I$![]() is generated by the finite set
is generated by the finite set
Indeed, let $c\in I\cap S_{\gamma }.$![]() There exists $\alpha \in Y_0$
There exists $\alpha \in Y_0$![]() such that $\alpha \geq \gamma$
such that $\alpha \geq \gamma$![]() and $\phi _{\alpha , \gamma }$
and $\phi _{\alpha , \gamma }$![]() is surjective. In particular, there exists $a\in S_{\alpha }$
is surjective. In particular, there exists $a\in S_{\alpha }$![]() such that $a\phi _{\alpha , \gamma }=c.$
such that $a\phi _{\alpha , \gamma }=c.$![]() Then $\gamma \in I_a,$
Then $\gamma \in I_a,$![]() so $\gamma =\beta \gamma$
so $\gamma =\beta \gamma$![]() for some $\beta \in X_a.$
for some $\beta \in X_a.$![]() It follows that
It follows that
completing the proof of this direction and of the theorem.
Corollary 7.16 Let $S=\mathcal {S}(Y,\, S_{\alpha },\, \phi _{\alpha , \beta })$![]() be a strong semilattice of completely simple semigroups. If $S$
be a strong semilattice of completely simple semigroups. If $S$![]() is weakly right noetherian, then the set $\{|S_{\alpha }/\mathcal {R}| : \alpha \in Y\}$
is weakly right noetherian, then the set $\{|S_{\alpha }/\mathcal {R}| : \alpha \in Y\}$![]() is bounded.
is bounded.
Proof. As in the proof of Lemma 7.14, we have that $S/\mathcal {R}$![]() is a strong semilattice of semigroups $\mathcal {S}(Y,\, T_{\alpha },\, \psi _{\alpha , \beta }),$
is a strong semilattice of semigroups $\mathcal {S}(Y,\, T_{\alpha },\, \psi _{\alpha , \beta }),$![]() where $T_{\alpha }=S_{\alpha }/\mathcal {R}$
where $T_{\alpha }=S_{\alpha }/\mathcal {R}$![]() . By Lemma 7.12, each $T_{\alpha }$
. By Lemma 7.12, each $T_{\alpha }$![]() is finite. Let $Y_0$
is finite. Let $Y_0$![]() be as stated in Theorem 7.15. We claim that $\{|T_{\alpha }| : \alpha \in Y\}$
be as stated in Theorem 7.15. We claim that $\{|T_{\alpha }| : \alpha \in Y\}$![]() is bounded above by
is bounded above by
Indeed, for each $\beta \in Y$![]() there exists $\alpha \in Y_0$
there exists $\alpha \in Y_0$![]() such that $\alpha \geq \beta$
such that $\alpha \geq \beta$![]() and $\psi _{\alpha , \beta } : T_{\alpha }\to T_{\beta }$
and $\psi _{\alpha , \beta } : T_{\alpha }\to T_{\beta }$![]() is surjective; thus $|T_{\beta }|\leq |T_{\alpha }|\leq N.$
is surjective; thus $|T_{\beta }|\leq |T_{\alpha }|\leq N.$![]()
Given Theorem 7.15, we can show that the converse of Proposition 7.12 does not hold, even in the case that $S$![]() is a band.
is a band.
Example 7.17 Let $S_i=\{x_i,\, y_i\}$![]() ($i\in \mathbb {N}$
($i\in \mathbb {N}$![]() ) be disjoint copies of the 2-element left zero semigroup. Let $\phi _{i, i}$
) be disjoint copies of the 2-element left zero semigroup. Let $\phi _{i, i}$![]() be the identity map on $S_i,$
be the identity map on $S_i,$![]() and for $i< j$
and for $i< j$![]() let $\phi _{i, j} : S_i\to S_j$
let $\phi _{i, j} : S_i\to S_j$![]() be the homomorphism given by $x_i\phi _{i, j}=y_i\phi _{i, j}=x_j.$
be the homomorphism given by $x_i\phi _{i, j}=y_i\phi _{i, j}=x_j.$![]() Then we have a strong semilattice of semigroups $S=\mathcal {S}(Y,\, S_i,\, \phi _{i, j}),$
Then we have a strong semilattice of semigroups $S=\mathcal {S}(Y,\, S_i,\, \phi _{i, j}),$![]() where $Y$
where $Y$![]() is the infinite descending chain $(\mathbb {N},\, \geq ).$
is the infinite descending chain $(\mathbb {N},\, \geq ).$![]() Clearly, $S$
Clearly, $S$![]() does not satisfy condition (3) of Theorem 7.15, so it is not weakly right noetherian.
does not satisfy condition (3) of Theorem 7.15, so it is not weakly right noetherian.
We end this section with an example demonstrating that Corollary 7.16 does not hold for completely regular semigroups in general.
Example 7.18 Let $S_i=\{x_{i,1},\, \ldots ,\, x_{i,i}\}$![]() for each $i\in \mathbb {N},$
for each $i\in \mathbb {N},$![]() and let $S=\bigcup _{i\in \mathbb {N}}S_i.$
and let $S=\bigcup _{i\in \mathbb {N}}S_i.$![]() For $i,\, j\in \mathbb {N},$
For $i,\, j\in \mathbb {N},$![]() $k\in \{1,\, \ldots ,\, i\}$
$k\in \{1,\, \ldots ,\, i\}$![]() and $l\in \{1,\, \ldots ,\, j\},$
and $l\in \{1,\, \ldots ,\, j\},$![]() define
define

It can be shown that this multiplication is associative by an exhaustive case analysis. It is easy to see that $S$![]() is a semilattice of semigroups $\mathcal {S}(Y,\, S_i),$
is a semilattice of semigroups $\mathcal {S}(Y,\, S_i),$![]() where $Y=(\mathbb {N},\, \geq )$
where $Y=(\mathbb {N},\, \geq )$![]() and each $S_i$
and each $S_i$![]() is a left zero semigroup.
is a left zero semigroup.
We now prove that $S$![]() is weakly right noetherian. Let $I$
is weakly right noetherian. Let $I$![]() be a right ideal of $S,$
be a right ideal of $S,$![]() and let $i$
and let $i$![]() be minimal such that $I\cap S_i\neq \emptyset .$
be minimal such that $I\cap S_i\neq \emptyset .$![]() We claim that $I=(I\cap S_i)S.$
We claim that $I=(I\cap S_i)S.$![]() Indeed, if $x_{j,l}\in I,$
Indeed, if $x_{j,l}\in I,$![]() then $j\geq i.$
then $j\geq i.$![]() If $i=j,$
If $i=j,$![]() then $x_{j,l}\in I\cap S_i.$
then $x_{j,l}\in I\cap S_i.$![]() Otherwise, we have $x_{j,l}=x_{i,1}x_{j,l}\in (I\cap S_i)S,$
Otherwise, we have $x_{j,l}=x_{i,1}x_{j,l}\in (I\cap S_i)S,$![]() as required.
as required.
8. Commutative semigroups
In this section, we consider weakly noetherian commutative semigroups. We begin by presenting the basic structure theory of commutative semigroups in terms of archimedean semigroups.
An archimedean semigroup is a commutative semigroup $S$![]() with the following property: for each $a, b\in S,$
with the following property: for each $a, b\in S,$![]() there exist $n\in \mathbb {N}$
there exist $n\in \mathbb {N}$![]() and $s\in S$
and $s\in S$![]() such that $a^{n}=bs.$
such that $a^{n}=bs.$![]() For instance, the free monogenic semigroup is archimedean.
For instance, the free monogenic semigroup is archimedean.
Theorem 8.1 Grillet [Reference Grillet11, Theorem IV.2.2]
Every commutative semigroup is a semilattice of archimedean semigroups.
We now characterize archimedean semigroups with an idempotent. We need the following definition.
A semigroup $S$![]() with zero $0$
with zero $0$![]() is said to be nilpotent if for every $s\in S$
is said to be nilpotent if for every $s\in S$![]() there exists $n\in \mathbb {N}$
there exists $n\in \mathbb {N}$![]() such that $s^{n}=0.$
such that $s^{n}=0.$![]()
Lemma 8.2 Grillet [Reference Grillet11, Proposition IV.2.3]
A semigroup $S$![]() is archimedean with idempotent if and only if $S$
is archimedean with idempotent if and only if $S$![]() is either an abelian group or an ideal extension of an abelian group by a commutative nilpotent semigroup.
is either an abelian group or an ideal extension of an abelian group by a commutative nilpotent semigroup.
In general, archimedean semigroups can have a rather complex structure. We refer the reader to [Reference Grillet11, Chapter IV] for more information.
In order for a commutative semigroup to be weakly noetherian, it is not necessary that all its archimedean components be weakly noetherian, as demonstrated by the following example.
Example 8.3 Let $FC_2$![]() denote the free commutative semigroup on two generators $a$
denote the free commutative semigroup on two generators $a$![]() and $b.$
and $b.$![]() We have that $FC_2$
We have that $FC_2$![]() is weakly noetherian by Theorem 3.8. It is easy to see that $FC_2$
is weakly noetherian by Theorem 3.8. It is easy to see that $FC_2$![]() has three archimedean components: $A=\langle a\rangle ,$
has three archimedean components: $A=\langle a\rangle ,$![]() $B=\langle b\rangle$
$B=\langle b\rangle$![]() and $C=\{a^{i}b^{j} : i,\, j\geq 1\}.$
and $C=\{a^{i}b^{j} : i,\, j\geq 1\}.$![]() The infinite set $\{ab^{i},\, a^{i}b : i\geq 1\}$
The infinite set $\{ab^{i},\, a^{i}b : i\geq 1\}$![]() consists of all the indecomposable elements of $C,$
consists of all the indecomposable elements of $C,$![]() so $C$
so $C$![]() is not weakly noetherian by Lemma 3.10.
is not weakly noetherian by Lemma 3.10.
The next example shows that a commutative semigroup may not be weakly noetherian even if its structure semilattice and archimedean components are all weakly noetherian.
Example 8.4 Let $S_i=\langle a_i\rangle$![]() ($i\in \mathbb {N}$
($i\in \mathbb {N}$![]() ) be disjoint copies of the free monogenic semigroup $\mathbb {N},$
) be disjoint copies of the free monogenic semigroup $\mathbb {N},$![]() which is weakly noetherian by Theorem 3.8. For $i< j,$
which is weakly noetherian by Theorem 3.8. For $i< j,$![]() let $\phi _{i, j} : S_i\to S_j$
let $\phi _{i, j} : S_i\to S_j$![]() be the isomorphism given by $a_i\mapsto a_j.$
be the isomorphism given by $a_i\mapsto a_j.$![]() Let $S$
Let $S$![]() be the strong semilattice of archimedean semigroups $\mathcal {S}(Y,\, S_i,\, \phi _{i, j}),$
be the strong semilattice of archimedean semigroups $\mathcal {S}(Y,\, S_i,\, \phi _{i, j}),$![]() where $Y=(\mathbb {N},\, \geq ).$
where $Y=(\mathbb {N},\, \geq ).$![]() Then $S$
Then $S$![]() contains an infinite set $\{a_i : i \in \mathbb {N}\}$
contains an infinite set $\{a_i : i \in \mathbb {N}\}$![]() of indecomposable elements, and is hence not weakly noetherian by Lemma 3.10.
of indecomposable elements, and is hence not weakly noetherian by Lemma 3.10.
We now state the main result of this section.
Theorem 8.5 Let $S$![]() be a commutative semigroup with finitely many archimedean components. Then $S$
be a commutative semigroup with finitely many archimedean components. Then $S$![]() is weakly noetherian if and only if $S/\mathcal {H}$
is weakly noetherian if and only if $S/\mathcal {H}$![]() is finitely generated.
is finitely generated.
Remark 8.6 Note that if $S$![]() is a commutative semigroup such that $S/\mathcal {H}$
is a commutative semigroup such that $S/\mathcal {H}$![]() is finitely generated, then $S$
is finitely generated, then $S$![]() has finitely many archimedean components. Indeed, let $S=\mathcal {S}(Y,\, S_{\alpha })$
has finitely many archimedean components. Indeed, let $S=\mathcal {S}(Y,\, S_{\alpha })$![]() be a decomposition of $S$
be a decomposition of $S$![]() into a semilattice of archimedean semigroups. It can be easily shown that if two elements of $S$
into a semilattice of archimedean semigroups. It can be easily shown that if two elements of $S$![]() are $\mathcal {H}$
are $\mathcal {H}$![]() -related, then they belong to the same archimedean component. Thus $S/\mathcal {H}=\mathcal {S}(Y,\, T_{\alpha })$
-related, then they belong to the same archimedean component. Thus $S/\mathcal {H}=\mathcal {S}(Y,\, T_{\alpha })$![]() for some semigroups $T_{\alpha }.$
for some semigroups $T_{\alpha }.$![]() Hence, $Y$
Hence, $Y$![]() is a homomorphic image of $S/\mathcal {H}.$
is a homomorphic image of $S/\mathcal {H}.$![]() Since $S/\mathcal {H}$
Since $S/\mathcal {H}$![]() is finitely generated, we conclude that $Y$
is finitely generated, we conclude that $Y$![]() is finite.
is finite.
It follows that Theorem 8.5 does not hold if the condition that $S$![]() has finitely many archimedean components is dropped, since there certainly exist weakly noetherian commutative semigroups with infinitely many archimedean components; e.g. infinite weakly noetherian semilattices.
has finitely many archimedean components is dropped, since there certainly exist weakly noetherian commutative semigroups with infinitely many archimedean components; e.g. infinite weakly noetherian semilattices.
In order to prove Theorem 8.5, we first state and prove a few lemmas.
Lemma 8.7 Let $T$![]() be a commutative nilpotent semigroup. If $T$
be a commutative nilpotent semigroup. If $T$![]() is finitely generated as a right ideal, then it is finite.
is finitely generated as a right ideal, then it is finite.
Proof. Since $T$![]() is finitely generated as a right ideal, there exists a finite set $X\subseteq T$
is finitely generated as a right ideal, there exists a finite set $X\subseteq T$![]() such that $T=XT^{1}.$
such that $T=XT^{1}.$![]() Let $U=\langle X\rangle .$
Let $U=\langle X\rangle .$![]() For each $x\in X,$
For each $x\in X,$![]() let
let
and let $N=\prod _{x\in X}m(x).$![]() It can be easily shown that $|U|\leq N.$
It can be easily shown that $|U|\leq N.$![]() We claim that $T=U.$
We claim that $T=U.$![]() Suppose for a contradiction that $T\neq U,$
Suppose for a contradiction that $T\neq U,$![]() and let $a\in T {\setminus} U.$
and let $a\in T {\setminus} U.$![]() We have that $a=x_1t_1$
We have that $a=x_1t_1$![]() for some $x_1\in X$
for some $x_1\in X$![]() and $t_1\in T^{1}.$
and $t_1\in T^{1}.$![]() Since $a\notin U,$
Since $a\notin U,$![]() we have that $t_1\in T {\setminus} U.$
we have that $t_1\in T {\setminus} U.$![]() By a similar argument, there exist $x_2\in X$
By a similar argument, there exist $x_2\in X$![]() and $t_2\in T {\setminus} U$
and $t_2\in T {\setminus} U$![]() such that $t_1=x_2t_2.$
such that $t_1=x_2t_2.$![]() Continuing in this way, for each $n\in \mathbb {N}$
Continuing in this way, for each $n\in \mathbb {N}$![]() there exist $x_1,\, \ldots ,\, x_n\in X$
there exist $x_1,\, \ldots ,\, x_n\in X$![]() and $t_n\in T {\setminus} U$
and $t_n\in T {\setminus} U$![]() such that $a=(x_1\cdots x_n)t_n.$
such that $a=(x_1\cdots x_n)t_n.$![]() However, we have that $x_1\cdots x_N=0$
However, we have that $x_1\cdots x_N=0$![]() and hence $a=0,$
and hence $a=0,$![]() which is a contradiction.
which is a contradiction.
Lemma 8.8 Let $S$![]() be an archimedean semigroup with idempotent. Then $S$
be an archimedean semigroup with idempotent. Then $S$![]() is weakly noetherian if and only if $S$
is weakly noetherian if and only if $S$![]() is either a group or an ideal extension of a group by a finite nilpotent semigroup.
is either a group or an ideal extension of a group by a finite nilpotent semigroup.
Proof. Every group is weakly noetherian, so assume that $S$![]() is not a group. By Lemma 8.2, there exists a group $G$
is not a group. By Lemma 8.2, there exists a group $G$![]() that is an ideal of $S$
that is an ideal of $S$![]() such that $T=S/G$
such that $T=S/G$![]() is a nilpotent semigroup. If $S$
is a nilpotent semigroup. If $S$![]() is weakly noetherian, it follows from Lemmas 4.1 and 8.7 that $T$
is weakly noetherian, it follows from Lemmas 4.1 and 8.7 that $T$![]() is finite. Conversely, if $T$
is finite. Conversely, if $T$![]() is finite, then $S$
is finite, then $S$![]() is weakly noetherian by Corollary 5.5.
is weakly noetherian by Corollary 5.5.
Lemma 8.9 Let $S$![]() be an archimedean semigroup without idempotent. Then $S$
be an archimedean semigroup without idempotent. Then $S$![]() is weakly noetherian if and only if it is finitely generated.
is weakly noetherian if and only if it is finitely generated.
Proof. The reverse implication follows from Theorem 3.8, so we just need to prove the direct implication.
Let $a$![]() be a fixed element of $S.$
be a fixed element of $S.$![]() The Tamura order on $S$
The Tamura order on $S$![]() (with respect to $a$
(with respect to $a$![]() ) is defined by
) is defined by
By [Reference Grillet11, Section IV.4], there exists a set $M$![]() of maximal elements of $S$
of maximal elements of $S$![]() (under $\leq _a$
(under $\leq _a$![]() ), where $a\in M,$
), where $a\in M,$![]() such that every element of $S$
such that every element of $S$![]() can be written in the form $p_n=a^{n}p$
can be written in the form $p_n=a^{n}p$![]() with $n\geq 0$
with $n\geq 0$![]() and $p\in M,$
and $p\in M,$![]() and the set $I=S {\setminus} M$
and the set $I=S {\setminus} M$![]() is an ideal. The Rees quotient $S/I$
is an ideal. The Rees quotient $S/I$![]() is nilpotent, since $S$
is nilpotent, since $S$![]() is an archimedean semigroup, and hence it is finite by Lemmas 4.1 and 8.7. Therefore, the set $M$
is an archimedean semigroup, and hence it is finite by Lemmas 4.1 and 8.7. Therefore, the set $M$![]() is finite and $S=\langle M\rangle$
is finite and $S=\langle M\rangle$![]() is finitely generated.
is finitely generated.
Lemma 8.10 Let $S$![]() be a weakly noetherian commutative semigroup with no non-trivial subgroups, and let $S=\mathcal {S}(Y,\, S_{\alpha })$
be a weakly noetherian commutative semigroup with no non-trivial subgroups, and let $S=\mathcal {S}(Y,\, S_{\alpha })$![]() be a decomposition of $S$
be a decomposition of $S$![]() into a semilattice of archimedean semigroups. Let $\beta \in Y$
into a semilattice of archimedean semigroups. Let $\beta \in Y$![]() and let $T$
and let $T$![]() be the subsemigroup $\bigcup _{\alpha \geq \beta }S_{\alpha }$
be the subsemigroup $\bigcup _{\alpha \geq \beta }S_{\alpha }$![]() of $S.$
of $S.$![]() Then there exists a finite set $X\subseteq S_{\beta }$
Then there exists a finite set $X\subseteq S_{\beta }$![]() such that $S_{\beta }=\langle X\rangle (T {\setminus} S_{\beta })^{1}.$
such that $S_{\beta }=\langle X\rangle (T {\setminus} S_{\beta })^{1}.$![]()
Proof. Since the complement of $T$![]() is an ideal of $S,$
is an ideal of $S,$![]() we have that $T$
we have that $T$![]() is weakly noetherian by Corollary 5.10. Note that $S_{\beta }$
is weakly noetherian by Corollary 5.10. Note that $S_{\beta }$![]() is an ideal of $T.$
is an ideal of $T.$![]()
Suppose first that $S_{\beta }$![]() has an idempotent. Then $S_{\beta }$
has an idempotent. Then $S_{\beta }$![]() is a nilpotent semigroup with zero $0.$
is a nilpotent semigroup with zero $0.$![]() Since $T$
Since $T$![]() is weaky noetherian, we have that $S_{\beta }=XT^{1}$
is weaky noetherian, we have that $S_{\beta }=XT^{1}$![]() for some finite set $X\subseteq S_{\beta } {\setminus} \{0\}.$
for some finite set $X\subseteq S_{\beta } {\setminus} \{0\}.$![]() Then $S_{\beta }=(XS_{\beta }^{1})(T {\setminus} S_{\beta })^{1}.$
Then $S_{\beta }=(XS_{\beta }^{1})(T {\setminus} S_{\beta })^{1}.$![]() By the same argument as the one in Lemma 8.7, we have that $XS_{\beta }^{1}$
By the same argument as the one in Lemma 8.7, we have that $XS_{\beta }^{1}$![]() is the finite semigroup $\langle X\rangle .$
is the finite semigroup $\langle X\rangle .$![]()
Now suppose that $S_{\beta }$![]() has no idempotent. Let $M$
has no idempotent. Let $M$![]() be the set of maximal elements of $S_{\beta }$
be the set of maximal elements of $S_{\beta }$![]() under the Tamura order with respect to an element $a\in S_{\beta },$
under the Tamura order with respect to an element $a\in S_{\beta },$![]() and let $I=S_{\beta } {\setminus} M.$
and let $I=S_{\beta } {\setminus} M.$![]() Then $I$
Then $I$![]() is an ideal of $T.$
is an ideal of $T.$![]() We have that $T/I$
We have that $T/I$![]() is weakly noetherian by Lemma 4.1, and $S_{\beta }/I$
is weakly noetherian by Lemma 4.1, and $S_{\beta }/I$![]() is a nilpotent semigroup with zero $0.$
is a nilpotent semigroup with zero $0.$![]() By the same argument as above, there exists a finite set $X\subseteq M=S_{\beta } {\setminus} \{0\}$
By the same argument as above, there exists a finite set $X\subseteq M=S_{\beta } {\setminus} \{0\}$![]() such that $S_{\beta }/I=\langle X\rangle (T {\setminus} S_{\beta })^{1}.$
such that $S_{\beta }/I=\langle X\rangle (T {\setminus} S_{\beta })^{1}.$![]() We may assume without loss of generality that $a\in X.$
We may assume without loss of generality that $a\in X.$![]() Since every element of $S_{\beta }$
Since every element of $S_{\beta }$![]() can be written as $a^{n}p$
can be written as $a^{n}p$![]() for some $n\geq 0$
for some $n\geq 0$![]() and $p\in M,$
and $p\in M,$![]() it follows that $S_{\beta }=\langle X\rangle (T {\setminus} S_{\beta })^{1}.$
it follows that $S_{\beta }=\langle X\rangle (T {\setminus} S_{\beta })^{1}.$![]()
Remark 8.11 Given Lemma 8.10, one might be tempted to think that in a weakly noetherian commutative semigroup with no non-trivial subgroups, every archimedean semigroup is contained in a finitely generated subsemigroup. However, this is not the case. Indeed, letting $Y=(\mathbb {N},\, \geq )$![]() and recalling Construction 6.8, we have that $U=\mathcal {U}(Y,\, \text {id})$
and recalling Construction 6.8, we have that $U=\mathcal {U}(Y,\, \text {id})$![]() is weakly noetherian by Proposition 6.9. Clearly, $U$
is weakly noetherian by Proposition 6.9. Clearly, $U$![]() is commutative. It can be easily shown that $U$
is commutative. It can be easily shown that $U$![]() is locally finite, so its infinite archimedean component $N_Y$
is locally finite, so its infinite archimedean component $N_Y$![]() is not contained in a finitely generated subsemigroup.
is not contained in a finitely generated subsemigroup.
We are now in a position to prove the main result of this section.
Proof of Theorem 8.5. ($\Rightarrow$![]() ) Let $S=\mathcal {S}(Y,\, S_{\alpha }),$
) Let $S=\mathcal {S}(Y,\, S_{\alpha }),$![]() where $Y$
where $Y$![]() is finite, be the decomposition of $S$
is finite, be the decomposition of $S$![]() into a semilattice of archimedean semigroups. Let $T$
into a semilattice of archimedean semigroups. Let $T$![]() denote the quotient $S/\mathcal {H}.$
denote the quotient $S/\mathcal {H}.$![]() Then $T$
Then $T$![]() is a semilattice of archimedean semigroups $\mathcal {S}(Y,\, T_{\alpha })$
is a semilattice of archimedean semigroups $\mathcal {S}(Y,\, T_{\alpha })$![]() where each $T_{\alpha }$
where each $T_{\alpha }$![]() is $\mathcal {H}$
is $\mathcal {H}$![]() -trivial. We have that $T$
-trivial. We have that $T$![]() is weakly noetherian by Lemma 4.1.
is weakly noetherian by Lemma 4.1.
We prove that $T$![]() is finitely generated by induction on $|Y|.$
is finitely generated by induction on $|Y|.$![]() Suppose that $|Y|=1,$
Suppose that $|Y|=1,$![]() so that $T$
so that $T$![]() is an archimedean semigroup. If $T$
is an archimedean semigroup. If $T$![]() has an idempotent, then it follows from Lemma 8.8 that $T$
has an idempotent, then it follows from Lemma 8.8 that $T$![]() is finite. If $T$
is finite. If $T$![]() has no idempotent, then $T\cong S$
has no idempotent, then $T\cong S$![]() is finitely generated by Lemma 8.9.
is finitely generated by Lemma 8.9.
Now suppose that $|Y|>1.$![]() Let $0$
Let $0$![]() be the minimal element of $Y.$
be the minimal element of $Y.$![]() By Lemma 8.10, there exists a finite set $X_0\subseteq T_0$
By Lemma 8.10, there exists a finite set $X_0\subseteq T_0$![]() such that $T_0=\langle X_0\rangle (T {\setminus} T_0)^{1}.$
such that $T_0=\langle X_0\rangle (T {\setminus} T_0)^{1}.$![]() Let $\alpha _1,\, \ldots ,\, \alpha _k$
Let $\alpha _1,\, \ldots ,\, \alpha _k$![]() be the elements of $Y$
be the elements of $Y$![]() that only $0$
that only $0$![]() is strictly less than. For each $i\in \{1,\, \ldots ,\, k\},$
is strictly less than. For each $i\in \{1,\, \ldots ,\, k\},$![]() define
define
We have that $T_i$![]() is a subsemigroup of $T$
is a subsemigroup of $T$![]() whose complement is an ideal, so it is weakly noetherian by Corollary 5.10. By the inductive hypothesis, $T_i$
whose complement is an ideal, so it is weakly noetherian by Corollary 5.10. By the inductive hypothesis, $T_i$![]() is generated by some finite set $X_i.$
is generated by some finite set $X_i.$![]() It follows that $T=\bigcup _{i=0}^{k}T_i$
It follows that $T=\bigcup _{i=0}^{k}T_i$![]() is generated by the finite set $\bigcup _{i=0}^{k}X_i,$
is generated by the finite set $\bigcup _{i=0}^{k}X_i,$![]() as required.
as required.
($\Leftarrow$![]() ) If $S/\mathcal {H}$
) If $S/\mathcal {H}$![]() is finitely generated, then it is weakly noetherian by Theorem 3.8, and hence $S$
is finitely generated, then it is weakly noetherian by Theorem 3.8, and hence $S$![]() is weakly noetherian by Lemma 4.3.
is weakly noetherian by Lemma 4.3.
From the proof of Theorem 8.5, we deduce a couple of corollaries. The first concerns complete semigroups; that is, commutative semigroups in which every archimedean component contains an idempotent.
Corollary 8.12 Let $S$![]() be a complete semigroup with finitely many idempotents. Then $S$
be a complete semigroup with finitely many idempotents. Then $S$![]() is weakly noetherian if and only if $S/\mathcal {H}$
is weakly noetherian if and only if $S/\mathcal {H}$![]() is finite.
is finite.
Proof. We have that $S/\mathcal {H}=\mathcal {S}(Y,\, T_{\alpha }),$![]() where $Y$
where $Y$![]() is finite and each $T_\alpha$
is finite and each $T_\alpha$![]() is a nilpotent semigroup. The direct implication is proved by a similar induction argument to the one in the proof of Theorem 8.5. Notice that $\langle X_0\rangle$
is a nilpotent semigroup. The direct implication is proved by a similar induction argument to the one in the proof of Theorem 8.5. Notice that $\langle X_0\rangle$![]() is finite, and also $T {\setminus} T_0$
is finite, and also $T {\setminus} T_0$![]() is finite since it is a finite union of semigroups that are finite by the inductive hypothesis. It follows that $T_0=\langle X_0\rangle (T {\setminus} T_0)^{1}$
is finite since it is a finite union of semigroups that are finite by the inductive hypothesis. It follows that $T_0=\langle X_0\rangle (T {\setminus} T_0)^{1}$![]() is finite, and hence $T=T_0\cup (T {\setminus} T_0)$
is finite, and hence $T=T_0\cup (T {\setminus} T_0)$![]() is finite.
is finite.
On the other extreme we have:
Corollary 8.13 Let $S$![]() be an idempotent-free commutative semigroup with finitely many archimedean components. Then $S$
be an idempotent-free commutative semigroup with finitely many archimedean components. Then $S$![]() is weakly noetherian if and only if it is finitely generated.
is weakly noetherian if and only if it is finitely generated.
Proof. This proof is essentially the same as that of Theorem 8.5, except we prove by induction that $S$![]() is finitely generated, rather than $S/\mathcal {H}.$
is finitely generated, rather than $S/\mathcal {H}.$![]()
We conclude this section by exhibiting an example of an idempotent-free commutative semigroup that is weakly noetherian but not finitely generated.
Example 8.14 For each $i\in \mathbb {N},$![]() let $S_i=\langle a_i\rangle$
let $S_i=\langle a_i\rangle$![]() be a copy of the free monogenic semigroup $\mathbb {N},$
be a copy of the free monogenic semigroup $\mathbb {N},$![]() and let $S$
and let $S$![]() be the disjoint union of the semigroups $S_i.$
be the disjoint union of the semigroups $S_i.$![]() Define a multiplication on $S,$
Define a multiplication on $S,$![]() extending those on each $S_i,$
extending those on each $S_i,$![]() as follows: for each $i,\, j,\, m,\, n\in \mathbb {N}$
as follows: for each $i,\, j,\, m,\, n\in \mathbb {N}$![]() with $i< j,$
with $i< j,$![]() let
let
It is easy to see that, with this multiplication, $S$![]() is an idempotent-free commutative semigroup. Moreover, we have that $S=\mathcal {S}(Y,\, S_i)$
is an idempotent-free commutative semigroup. Moreover, we have that $S=\mathcal {S}(Y,\, S_i)$![]() where $Y=(\mathbb {N},\, \geq ).$
where $Y=(\mathbb {N},\, \geq ).$![]() Since $Y$
Since $Y$![]() is infinite, $S$
is infinite, $S$![]() is not finitely generated. It can be easily shown that every ideal of $S$
is not finitely generated. It can be easily shown that every ideal of $S$![]() has the form
has the form

for some $i,\, m\in \mathbb {N}.$![]() In particular, every ideal of $S$
In particular, every ideal of $S$![]() is principal, so $S$
is principal, so $S$![]() is weakly noetherian.
is weakly noetherian.
Acknowledgements
This research was supported by the London Mathematical Society through the Early Career Fellowship scheme. The author would like to thank the referee for their helpful comments and suggestions, which improved the quality of the article. The author is also grateful to Victoria Gould for her support, and in particular for comments that led to Theorem 3.2, Proposition 4.9 and Theorem 6.24.