Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T01:16:43.649Z Has data issue: false hasContentIssue false
  • English
  • Français

Semigroups of left quotients—the uniqueness problem

Published online by Cambridge University Press:  20 January 2009

Victoria Gould
Victoria Gould
Affiliation:
Department of MathematicsUniversity of YorkHeslingtonYork, YO1 5DD
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S be a subsemigroup of a semigroup Q. Then Q is a semigroup of left quotients of S if every element of Q can be written as a*b, where a lies in a group 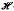-class of Q and a* is the inverse of a in this group; in addition, we insist that every element of S satisfying a weak cancellation condition named square-cancellable lie in a subgroup of Q.

J. B. Fountain and M. Petrich gave an example of a semigroup having two non-isomorphic semigroups of left quotients. More positive results are available if we restrict the classes of semigroups from which the semigroups of left quotients may come. For example, a semigroup has at most one bisimple inverse ω-semigroup of left quotients. The crux of the matter is the restrictions to a semigroup S of Green's relations ℛ and ℒ in a semigroup of quotients of S. With this in mind we give necessary and sufficient conditions for two semigroups of left quotients of S to be isomorphic under an isomorphism fixing S pointwise.

The above result is then used to show that if R is a subring of rings Q1 and Q2 and the multiplicative subsemigroups of Q1 and Q2 are semigroups of left quotients of the multiplicative semigroup of R, then Ql and Q2 are isomorphic rings.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 35 , Issue 2 , June 1992 , pp. 213 - 226
Copyright
Copyright © Edinburgh Mathematical Society 1992

References

REFERENCES

1.Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups (Math. Surveys 7, Vols. I and II, American Math. Soc. 1961, 1967).CrossRefGoogle Scholar
2.Fountain, J. B., Abundant semigroups, Proc. London Math. Soc. 44 (1982), 103–129.CrossRefGoogle Scholar
3.Fountain, J. B. and Gould, V. A. R., Orders in rings without identity, Preprint.Google Scholar
4.Fountain, J. B. and Gould, V. A. R., Straight left orders in rings, Preprint.Google Scholar
5.Fountain, J. B. and Gould, V. A. R., Orders in regular rings with minimal condition for principal right ideals, Preprint.Google Scholar
6.Fountain, J. B. and Petrich, M., Completely 0-simple semigroups of quotients, J. Algebra 101 (1986), 365–402.CrossRefGoogle Scholar
7.Gould, V. A. R., Semigroups of Quotients (D.Phil, thesis, University of York, 1985).Google Scholar
8.Gould, V. A. R., Bisimple inverse ω-semigroups of left quotients, Proc. London Math. Soc. 52 (1986), 95–118.CrossRefGoogle Scholar
9.Gould, V. A. R., Orders in Semigroups (Contributions to General Algebra 5, Holder-Pichler-Tempsky, Wien, 1987).Google Scholar
10.Gould, V. A. R., Semigroups of Quotients (Proceedings of the International Symposium on the Theory of Regular Semigroups and Applications, University of Kerala, 1986).Google Scholar
11.Howie, J. M., An Introduction to Semigroup Theory (Academic Press, 1976).Google Scholar
12.Lambek, J., Lectures on Rings and Modules (Blaisdell Publishing Co., 1966).Google Scholar