No CrossRef data available.
Published online by Cambridge University Press: 18 December 2024
Here we consider the discrete time dynamics described by a transformation 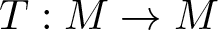 $T:M \to M$, where T is either the action of shift
$T:M \to M$, where T is either the action of shift 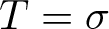 $T=\sigma$ on the symbolic space
$T=\sigma$ on the symbolic space 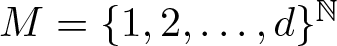 $M=\{1,2, \ldots,d\}^{\mathbb{N}}$, or, T describes the action of a d to 1 expanding transformation
$M=\{1,2, \ldots,d\}^{\mathbb{N}}$, or, T describes the action of a d to 1 expanding transformation 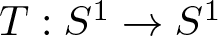 $T:S^1 \to S^1$ of class
$T:S^1 \to S^1$ of class 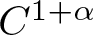 $C^{1+\alpha}$ (for example
$C^{1+\alpha}$ (for example 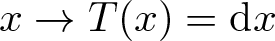 $x \to T(x) =\mathrm{d} x $ (mod 1)), where
$x \to T(x) =\mathrm{d} x $ (mod 1)), where 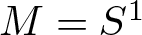 $M=S^1$ is the unit circle. It is known that the infinite-dimensional manifold
$M=S^1$ is the unit circle. It is known that the infinite-dimensional manifold  $\mathcal{N}$ of Hölder equilibrium probabilities is an analytical manifold and carries a natural Riemannian metric. Given a certain normalized Hölder potential A denote by
$\mathcal{N}$ of Hölder equilibrium probabilities is an analytical manifold and carries a natural Riemannian metric. Given a certain normalized Hölder potential A denote by 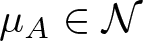 $\mu_A \in \mathcal{N}$ the associated equilibrium probability. The set of tangent vectors X (functions
$\mu_A \in \mathcal{N}$ the associated equilibrium probability. The set of tangent vectors X (functions 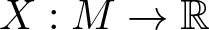 $X: M \to \mathbb{R}$) to the manifold
$X: M \to \mathbb{R}$) to the manifold  $\mathcal{N}$ at the point µA (a subspace of the Hilbert space
$\mathcal{N}$ at the point µA (a subspace of the Hilbert space 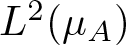 $L^2(\mu_A)$) coincides with the kernel of the Ruelle operator for the normalized potential A. The Riemannian norm
$L^2(\mu_A)$) coincides with the kernel of the Ruelle operator for the normalized potential A. The Riemannian norm 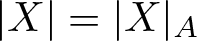 $|X|=|X|_A$ of the vector X, which is tangent to
$|X|=|X|_A$ of the vector X, which is tangent to  $\mathcal{N}$ at the point µA, is described via the asymptotic variance, that is, satisfies
$\mathcal{N}$ at the point µA, is described via the asymptotic variance, that is, satisfies
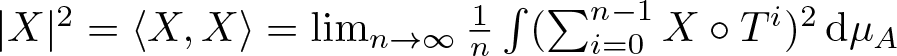 $ |X|^2 = \langle X, X \rangle = \lim_{n \to \infty}\frac{1}{n} \int (\sum_{i=0}^{n-1} X\circ T^i )^2 \,\mathrm{d} \mu_A$.
$ |X|^2 = \langle X, X \rangle = \lim_{n \to \infty}\frac{1}{n} \int (\sum_{i=0}^{n-1} X\circ T^i )^2 \,\mathrm{d} \mu_A$.
Consider an orthonormal basis Xi, 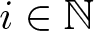 $i \in \mathbb{N}$, for the tangent space at µA. For any two orthonormal vectors X and Y on the basis, the curvature
$i \in \mathbb{N}$, for the tangent space at µA. For any two orthonormal vectors X and Y on the basis, the curvature 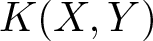 $K(X,Y)$ is
$K(X,Y)$ is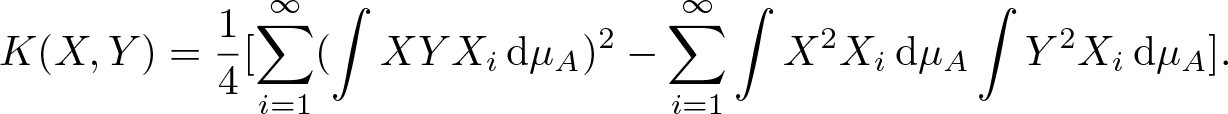 \begin{equation*}K(X,Y) = \frac{1}{4}[ \sum_{i=1}^\infty (\int X Y X_i \,\mathrm{d} \mu_A)^2 - \sum_{i=1}^\infty \int X^2 X_i \,\mathrm{d} \mu_A \int Y^2 X_i \,\mathrm{d} \mu_A ].\end{equation*}
\begin{equation*}K(X,Y) = \frac{1}{4}[ \sum_{i=1}^\infty (\int X Y X_i \,\mathrm{d} \mu_A)^2 - \sum_{i=1}^\infty \int X^2 X_i \,\mathrm{d} \mu_A \int Y^2 X_i \,\mathrm{d} \mu_A ].\end{equation*}
When the equilibrium probabilities µA is the set of invariant Markov probabilities on 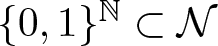 $\{0,1\}^{\mathbb{N}}\subset \mathcal{N}$, introducing an orthonormal basis
$\{0,1\}^{\mathbb{N}}\subset \mathcal{N}$, introducing an orthonormal basis 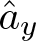 $\hat{a}_y$, indexed by finite words y, we show explicit expressions for
$\hat{a}_y$, indexed by finite words y, we show explicit expressions for 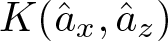 $K(\hat{a}_x,\hat{a}_z)$, which is a finite sum. These values can be positive or negative depending on A and the words x and z. Words
$K(\hat{a}_x,\hat{a}_z)$, which is a finite sum. These values can be positive or negative depending on A and the words x and z. Words  $x,z$ with large length can eventually produce large negative curvature
$x,z$ with large length can eventually produce large negative curvature 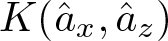 $K(\hat{a}_x,\hat{a}_z)$. If
$K(\hat{a}_x,\hat{a}_z)$. If 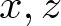 $x, z$ do not begin with the same letter, then
$x, z$ do not begin with the same letter, then 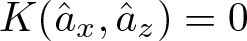 $K(\hat{a}_x,\hat{a}_z)=0$.
$K(\hat{a}_x,\hat{a}_z)=0$.
Partially supported by CNPq