No CrossRef data available.
Published online by Cambridge University Press: 03 November 2023
Let 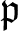 $\mathfrak{p}$ be a prime ideal in a commutative noetherian ring R and denote by
$\mathfrak{p}$ be a prime ideal in a commutative noetherian ring R and denote by 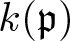 $k(\mathfrak{p})$ the residue field of the local ring
$k(\mathfrak{p})$ the residue field of the local ring 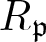 $R_\mathfrak{p}$. We prove that if an R-module M satisfies
$R_\mathfrak{p}$. We prove that if an R-module M satisfies 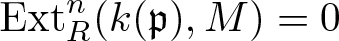 $\operatorname{Ext}_R^{n}(k(\mathfrak{p}),M)=0$ for some
$\operatorname{Ext}_R^{n}(k(\mathfrak{p}),M)=0$ for some 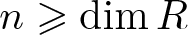 $n\geqslant\dim R$, then
$n\geqslant\dim R$, then 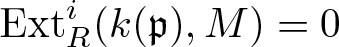 $\operatorname{Ext}_R^i(k(\mathfrak{p}),M)=0$ holds for all
$\operatorname{Ext}_R^i(k(\mathfrak{p}),M)=0$ holds for all 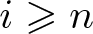 $i \geqslant n$. This improves a result of Christensen, Iyengar and Marley by lowering the bound on n. We also improve existing results on Tor-rigidity. This progress is driven by the existence of minimal semi-flat-cotorsion replacements in the derived category as recently proved by Nakamura and Thompson.
$i \geqslant n$. This improves a result of Christensen, Iyengar and Marley by lowering the bound on n. We also improve existing results on Tor-rigidity. This progress is driven by the existence of minimal semi-flat-cotorsion replacements in the derived category as recently proved by Nakamura and Thompson.