No CrossRef data available.
Published online by Cambridge University Press: 03 April 2023
In this paper, we obtain one sharp estimate for the length 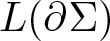 $L(\partial\Sigma)$ of the boundary
$L(\partial\Sigma)$ of the boundary 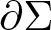 $\partial\Sigma$ of a capillary minimal surface Σ2 in M3, where M is a compact three-manifolds with strictly convex boundary, assuming Σ has index one. The estimate is in term of the genus of Σ, the number of connected components of
$\partial\Sigma$ of a capillary minimal surface Σ2 in M3, where M is a compact three-manifolds with strictly convex boundary, assuming Σ has index one. The estimate is in term of the genus of Σ, the number of connected components of 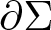 $\partial\Sigma$ and the constant contact angle θ. Making an extra assumption on the geometry of M along
$\partial\Sigma$ and the constant contact angle θ. Making an extra assumption on the geometry of M along 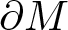 $\partial M$, we characterize the global geometry of M, which is saturated only by the Euclidean three-balls. For capillary stable CMC surfaces, we also obtain similar results.
$\partial M$, we characterize the global geometry of M, which is saturated only by the Euclidean three-balls. For capillary stable CMC surfaces, we also obtain similar results.