On p. 403 of Greenhill's Calculus (2nd Ed.) the following sentence occurs:— “By differentiation of the integral

with respect to A, B, or C we can deduce the results of

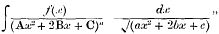
For the evaluation of tlie typical form in which f(x) is a linear function, especially when A, B, etc., are given numbers, the method of differentiation does not seem very suitable; be that as it may, it may perhaps be of some interest to investigate a formula of reduction analogous to those in use for the integrals in which Ax2 + 2Bx + C is replaced by a linear function and f(x) is a constant.