Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T07:01:57.024Z Has data issue: false hasContentIssue false
  • English
  • Français

Real interpolation for divisible cones

Published online by Cambridge University Press:  20 January 2009

María J. Carro ,
Stefan Ericsson  and
Lars-Erik Persson
María J. Carro
Affiliation:
Departament de Matemàtica Aplicada i AnàlisiUniversitat de Barcelona, 08071 Barcelona, Spain, E-mail address: [email protected]
Stefan Ericsson
Affiliation:
Departament de Matemàtica Aplicada i AnàlisiUniversitat de Barcelona, 08071 Barcelona, Spain, E-mail address: [email protected]
Lars-Erik Persson
Affiliation:
Department of Mathematics, Luleå University, S-971 87 Luleå, Sweden, E-mail addresses: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give necessary and sufficient conditions on a general cone of positive functions to satisfy the Decomposition Property (DP) introduced in [5] and connect the results with the theory of interpolation of cones introduced by Sagher [9]. One of our main result states that if Q satisfies DP or equivalently is divisible, then for the quasi-normed spaces E0 and E1,

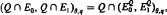
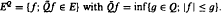
According to this formula, it yields that the interpolation theory for divisible cones can be easily obtained from the classical theory.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 42 , Issue 2 , June 1999 , pp. 285 - 304
Copyright
Copyright © Edinburgh Mathematical Society 1999

References

REFERENCES

1.Asekritova, I. U., The Holmstedt formula and an equivalence theorem for N-set of Banach spaces, Yaroslav Gos. Univ. 165 (1980), 15–18.Google Scholar
2.Bergh, J. and Löfström, J., Interpolation Spaces. An Introduction (Grundlehren der Mathematischen Wissenschaften 223, Springer Verlag, Berlin-Heidelberg-New York, 1976).CrossRefGoogle Scholar
3.Brudnyi, Yu. A. and Krugljak, N. Ya., Interpolation Functors and Interpolation Spaces (North Holland, 1991).Google Scholar
4.Carro, M. J., Ericsson, S. and Persson, L. E., S-divisibility property and a Holmstedt type formula, J. Approx. Th., to appear.Google Scholar
5.Cerdà, J. and Martin, J., Interpolation of operators on decreasing functions, Math. Scand. 78 (1996), 233–245.CrossRefGoogle Scholar
6.Cerdà, J. and Martin, J., Interpolation restricted to decreasing functions and Lorentz spaces, Preprint (1996).Google Scholar
7.Ericsson, S., Exact descriptions of some K and E functionals, J. Approx. Th. 90 (1997), 75–87.CrossRefGoogle Scholar
8.Nilsson, P., Reiteration theorems for real interpolation and approximation spaces, Ann. Math. Pura Appl. 132 (1982), 291–330.CrossRefGoogle Scholar
9.Sagher, Y., An application of interpolation theory to Fourier series, Studia Math. (1972), 169–181.CrossRefGoogle Scholar