Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T11:00:31.289Z Has data issue: false hasContentIssue false
  • English
  • Français

The Radon-Nikodym Theorem for Multimeasures

Published online by Cambridge University Press:  20 January 2009

Le van Tu
Le van Tu
Affiliation:
University of Western Australia, Nedlands, W.A. 6009., Australia.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (S, ℳ) be a measurable space (that is, a set S in which is defined a σ-algebra ℳ of subsets) and X a locally convex space. A map M from ℳ to the family of all non-empty subsets of X is called a multimeasure iff for every sequence of disjoint sets An ɛ ℳ (n=1,2,… )with 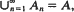the series 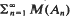converges (in the sense of (6), p. 3) to M(A).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 21 , Issue 2 , September 1978 , pp. 167 - 173
Copyright
Copyright © Edinburgh Mathematical Society 1978

References

REFERENCES

(1) Castaing, C., Sur les multiapplications mesurables, Rev. Française Inform. Recherche Opérationnelle 1 (1967), 91–126.Google Scholar
(2) Castaing, C. and Valadier, M., Équations différentielles multivoques dans les espaces vectoriels localement convexes, Rev. Française Inform. Recherche Opérationnelle 16 (1969), 3–16.Google Scholar
(3) Coste, A., Applications de la théorie des probabilités cylindriques et des opérateurs radonifiants à l'étude des fonctions aléatoires sous-linéaires et des multimesures, C.R. Acad. Sci. Paris, 282, Série A (1976), 103–106.Google Scholar
(4) Himmelberg, C. J. and Van Vleck, F. S., Some selection theorems for measurable functions, Canadian J. Math. 21 (1969), 394–399.CrossRefGoogle Scholar
(5) Hörmander, L., Sur la fonction d'appui des ensembles convexes dans un espace localement convexe, Arkiv för Mat. 3 (1954), 181–186.CrossRefGoogle Scholar
(6) Kluvánek, I. and Knowles, G., Vector measures and control systems (North-Holland, Amsterdam, 1975).Google Scholar
(7) Leese, S. J., Set-valued functions and selectors, (Ph.D. thesis, University of Keele, 1974).Google Scholar
(8) Meyer, P. A., Probabilites et potentiel (Hermann, Paris, 1966).Google Scholar
(9) Pettis, B. J., On integration in vector spaces, Trans. Amer. Math. Soc. 44 (1938), 277–304.CrossRefGoogle Scholar
(10) Robertson, A. P., On measurable selections, Proc. Roy. Soc. Edinburgh, (A) 72 (1974), 1–7.CrossRefGoogle Scholar
(11) Tolstonogov, A. A., On the theorems of Radon-Nikodym and A. A. Ljapunov for a multivalued measure, Soviet Math. Dokl., 16 (1975), 1588–1592 (Dokl. Akad. Nauk SSSR, 225 (1975), 1023-1026).Google Scholar
(12) Tu, L. V., Omega-Polish spaces and measurable selections, J. Australian Math. Soc. (Series A) 23 (1977), 257–265.CrossRefGoogle Scholar
(13) Tu, L. V., On multifunctions and multimeasures, (Ph.D. thesis, Murdoch University, 02 1977).Google Scholar
(14) Valadier, M., Misapplications mesurables a valeurs convexes compactes, J. Math, pures et appl, 50 (1971), 265–297.Google Scholar
(15) Vind, K., Edgeworth-allocations in an exchange economy with many traders, Internal. Econ. Review 5 (1964), 165–177CrossRefGoogle Scholar