Published online by Cambridge University Press: 30 April 2018
We are concerned with the existence of positive weak solutions, as well as the existence of bound states (i.e. solutions in W1, p (ℝN)), for quasilinear scalar field equations of the form
where Δpu: = div(|∇ u|p−2∇u), 1 < p < N, p*: = Np/(N − p) is the critical Sobolev exponent, q ∈ (p, p*), while V(·) and K(·) are non-negative continuous potentials that may decay to zero as |x| → ∞ but are free from any integrability or symmetry assumptions.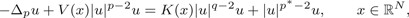 $$ - \Delta _pu + V(x) \vert u \vert ^{p - 2}u = K(x) \vert u \vert ^{q - 2}u + \vert u \vert ^{p^ * - 2}u,\qquad x \in {\open R}^N,$$
$$ - \Delta _pu + V(x) \vert u \vert ^{p - 2}u = K(x) \vert u \vert ^{q - 2}u + \vert u \vert ^{p^ * - 2}u,\qquad x \in {\open R}^N,$$